Задачи, функции и принципы прогнозирования

Задачи, функции и принципы прогнозирования

Экономическое прогнозирование призвано решать двуединую задачу: с одной стороны, давать объективную научно обоснованную картину будущего, опираясь на процессы сегодняшнего дня, а с другой - выбирать направление деятельности и политики современности с учетом прогнозных оценок. Наряду с этим важной задачей прогнозирования можно назвать выявление в настоящем тех факторов, которые будут оказывать свое влияние на исследуемый процесс в будущем.

Главная функция прогнозирования состоит в проведении научного анализа социально-экономических процессов и тенденций, а также в предвидении новых экономических ситуаций и выявлении узловых экономических проблем. Основные функции прогнозирования состоят также в исследовании объективных связей социально-экономических явлений и процессов в конкретных условиях, на определенном этапе развития экономики и общества, в оценке объекта прогнозирования, в выявлении возможных альтернатив развития экономики в перспективе, в принятии оптимальных решений.

Принципы прогнозирования меняются в зависимости от экономических условий, которые существуют на том или ином историческом этапе развития общества. В частности, со сменой социально-экономического строя в нашей стране ушли такие принципы, как партийность прогнозирования, принцип сочетания политики и экономики, принцип директивности планирования.

В рыночных условиях среди основных принципов, на которых базируется процесс прогнозирования, можно выделить следующие:

1) научная обоснованность прогноза (разработка с помощью научных методов, с учетом закономерности развития природы, общества и мышления);

2) непрерывность прогнозирования (прогноз должен постоянно корректироваться с учетом изменения ситуации в стране, экономике);

3) сочетание перспективного и текущего прогнозирования (данные виды прогнозирования осуществляются во взаимосвязи, но приоритет отдается перспективному прогнозированию);

4) согласованность прогнозов (разработанный прогноз должен быть взаимосвязан со смежными прогнозами);

5) многовариантность, альтернативность прогноза (рекомендуется разрабатывать несколько вариантов прогноза, чтобы в случае изменения ситуации использовать другой вариант. Обычно существует три варианта прогноза: оптимистичный, пессимистичный, реалистичный);

6) выбор основных факторов (при прогнозировании должны быть заложены в расчеты основные факторы, оказывающие влияние на исследуемый процесс. Это особенно актуально потому, что экономические процессы сложные, многофакторные и учесть влияние всех факторов невозможно);

7) системность разработки прогноза (процесс прогнозирования следует рассматривать, с одной стороны, как единую целостную систему, а с другой - как сложную систему, состоящую из отдельных самостоятельных блоков);

8) верифицированность прогнозов (прогнозные оценки должны быть достоверны и обоснованны);

9) адекватность (максимальное приближение прогнозной модели к реальной действительности, тенденциям, закономерностям);

10) рентабельность (эффект от разработанного прогноза должен превышать затраты на его разработку).

Принципы прогнозирования обеспечивают методологическое единство разнообразных методов и моделей прогнозирования.

Этапы прогнозирования

Все формальные процедуры прогнозирования предусматривают перенос прошлого опыта в неопределенное будущее. Таким образом, все они построены на предположении, что условия, породившие полученные ранее данные, неотличимы от условий будущего. Исключение составляют только те переменные, которые точно распознаны моделью прогнозирования. Например, если кто-то строит прогноз показателей производительности служащих, исходя только из множества оценок, выставленных им при испытаниях в процессе приема на работу, то он, очевидно, предполагает, что показатель производительности каждого работника зависит только от них. В действительности же подобное предположение о неразличимости прошлого и будущего не выполняется в полной мере. Поэтому полученный прогноз будет неточен, если только он не будет модифицирован на основании оценки, выполненной составителем прогноза.

Можно выделить следующие пять этапов в процессе прогнозирования.

1. Сбор данных

2. Редукция или уплотнение данных

3. Построение модели и ее оценка

4. Экстраполяция выбранной модели (фактический прогноз)

5. Оценка полученного прогноза

Этап 1, сбор данных, предполагает получение корректных данных и обязательную проверку того, что они верны. Этот этап часто является наиболее сомнительной частью всего процесса прогнозирования и в то же время наиболее сложен для проверки, поскольку последующие этапы с одинаковым успехом могут производиться с использованием данных, как соответствующих изучаемой проблеме, так и не соответствующих ей. Всякий раз, когда возникает необходимость получить в организации определенные данные, их сбор и проверка обязательно сопровождаются множеством различных проблем.
Этап 2, редукция или уплотнение данных, часто оказывается необходимым, так как для выполнения прогнозирования может быть собрано как слишком много исходных данных, так и слишком мало. Некоторые данные могут не иметь прямого отношения к рассматриваемой задаче, а будут лишь снижать точность прогнозирования.
Этап 3, построение модели и ее оценка, состоит в подборе модели прогноза, наиболее соответствующей особенностям собранных данных в смысле минимизации ошибки прогноза. Чем проще модель, тем лучше она будет воспринята менеджерами фирмы, ответственными за принятие решения, и тем выше будет их доверие к полученному прогнозу. Часто следует отдавать предпочтение не более сложному подходу к прогнозированию, предлагающему немного больше точности, а более простому, понятному руководителям компании. Когда выбранный метод получает поддержку у менеджеров, то и результаты прогнозирования активно ими используются.
Этап 4, экстраполяция выбранной модели, предусматривает фактическое получение требуемого прогноза, поскольку необходимые данные уже собраны и, возможно, редуцированы, а соответствующая модель прогноза определена. Часто для проверки точности получаемых результатов применяется прогнозирование на недавно прошедшие периоды, для которых исследуемые величины уже известны. Наблюдаемые ошибки затем определенным образом анализируются. Эта процедура обсуждается ниже, при описании этапа 5.
Этап 5, оценка полученного прогноза, состоит в сравнении вычисленных величин с действительно наблюдаемыми значениями. Для этой цели часть наиболее свежей фактической информации обычно исключается из множества анализируемых данных. После того как модель прогноза будет подобрана, выполняется прогноз на эти периоды и полученные результаты сравниваются с известными наблюдаемыми значениями. Некоторые процедуры прогнозирования предусматривают суммирование абсолютных значений ошибок и представляют либо эту сумму, либо частное от деления ее на число прогнозируемых значений, представляющее собой значение средней ошибки прогноза. Другие процедуры используют сумму квадратов ошибок, которая затем сравнивается с аналогичными числами, полученными для альтернативных методов прогнозирования. Некоторые процедуры отслеживают и отмечают величину пределов ошибки за период прогнозирования.

Методы экспертных оценок

Интуитивные методы прогнозированияприменяются для тех процессов, которые невозможно описать математическими формулами. Использование данных методов дает возможность получить прогнозную оценку состояния развития объекта в будущем независимо от информационной обеспеченности. Сущность интуитивных методов заключается в построении рациональной процедуры интуитивно-логического мышления человека в сочетании с количественными методами оценки и обработки полученных результатов. Решение проблемы в этом случае базируется на обобщенном мнении экспертов.

Методы экспертных оценок широко применяются на практике и имеют характерные особенности: 1) научно обоснованная организация проведения всех этапов экспертизы, обеспечивающая наибольшую эффективность работы на каждом этапе; 2) применение количественных методов как при организации экспертизы, так и при оценке суждений экспертов и формальной групповой обработке результатов.

Организация процедуры экспертной оценки включает несколько этапов: формирование репрезентативной экспертной группы; подготовку и проведение экспертизы; статистическую обработку полученных результатов опроса.

Методы отбора экспертов.В практике прогнозирования нередки случаи, когда количественная информация об объекте либо отсутствует, либо носит ограниченный характер. В этих условиях применение формализованных методов затруднено, им на смену приходят интуитивные методы или экспертные оценки.

Слово «эксперт» - латинского происхождения и означает опытный, сведущий. Интуитивные методы в отличие от формализованных появились очень давно. Один из наиболее распространенных интуитивных методов - метод Дельфи - получил свое название по названию города Дельфы, который прославился своими мудрецами и предсказателями, жившими в нем еще до нашей эры. Формализованные методы разработаны и нашли свое применение лишь в ХХ веке.

На способность эксперта строить прогноз оказывают влияние внутренние и внешние факторы. Внутренние факторы зависят от индивидуальных качеств эксперта, т.е. от его опыта, знаний, интеллекта, способности предвидеть будущее. Внешние факторы- это те, которые в значительной степени не зависят от личности эксперта, а определяются внешними условиями, ограничениями, например, степенью доступа эксперта к информации; правильностью постановки задаваемых вопросов; погрешностью модели опроса.

При отборе экспертов, как правило, необходимо руководствоваться следующими основными критериями:

1)степень компетентности эксперта. При ее оценке следует учитывать должностное положение эксперта, ученое звание, количество опубликованных работ, количество ссылок на эти работы;

2) стаж работ эксперта в области, связанной с объектом прогнозирования;

3) устойчивость взглядов кандидата в эксперты, умение отстаивать свои позиции и преодолевать ранее сложившиеся стереотипы;

4) способность к нелинейному мышлению, к рассмотрению проблемы с разных сторон, с разных позиций.

Из всего разнообразия методов отбора экспертов можно выделить:

а) документальный метод - предусматривает подбор экспертов с учетом их научных знаний, стажа работы, возраста, количества публикаций и ссылок на них, т.е. изучается вся документально подтверждаемая информация о кандидате в эксперты;

б) экспериментальный метод - заключается в проверке эффективности работы эксперта в прошлом;

в) метод самооценки –эксперту предлагается самостоятельно оценить свою компетентность в области объекта прогнозирования;

г) методы голосования (имеют несколько разновидностей: прием исключения, попарное сравнение кандидатов, метод «приятелей»).

Прием исключения. Несколько специально подобранных выборщиков (специалистов) составляют предварительный список кандидатов. Организаторы изучают его, выделяя наиболее ценные кандидатуры.

Попарное сравнение кандидатов. Из предварительного списка берется произвольно два кандидата, и при сравнении один из них обязательно исключается.

Метод «приятелей» предполагает отбор экспертов из числа знакомых. Эксперты-выборщики предлагают свои кандидатуры, дальше эти кандидаты предлагают свои кандидатуры - нарастание числа потенциальных кандидатов происходит по принципу «снежного кома».

В зависимости от организации экспертной оценки и формы опроса экспертов различают методы индивидуальных и коллективных экспертных оценок.

Методика прогнозирования

Прогнозные оценки с помощью методов экстраполяции рассчитываются в несколько этапов:

- проверка базовой линии прогноза;

- выявление закономерностей прошлого развития явления;

- оценка степени достоверности выявленной закономерности развития явления в прошлом (подбор трендовой функции);

- экстраполяция — перенос выявленных закономерностей на некоторый период будущего;

- корректировка полученного прогноза с учётом результатов содержательного анализа текущего состояния.

Для получения объективного прогноза развития изучаемого явления данные базовой линии должны соответствовать следующим требованиям:

- шаг по времени для всей базовой линии должен быть одинаков;

- наблюдения фиксируются в один и тот же момент каждого временного отрезка (например, на полдень каждого дня, первого числа каждого месяца);

- базовая линия должна быть полной, то есть пропуск данных не допускается.

Если в наблюдениях отсутствуют результаты за незначительный отрезок времени, то для обеспечения полноты базовой линии необходимо их восполнить приблизительными данными, например, использовать среднее значение соседних отрезков.

Корректировка полученного прогноза выполняется для уточнения полученных долгосрочных прогнозов с учётом влияния сезонности или скачкообразности развития изучаемого явления.

Явления общественной жизни, изучаемые социально-экономической статистикой, находятся в непрерывном изменении и развитии. С течением времени – от месяца к месяцу, от года к году – изменяются численность населения и его состав, объем производимой продукции, уровень производительности труда и т. д., поэтому одной из важнейших задач статистики является изучение изменения общественных явлений во времени – процесса их развития, их динамики. Эту задачу статистика решает путем построения и анализа рядов динамики (временных рядов).

Ряд динамики (хронологический, динамический, временной ряд) – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд включает два обязательных элемента: время и конкретное значение показателя (уровень ряда).

Каждое числовое значение показателя, характеризующее величину, размер явления, называется уровнем ряда. Кроме уровней каждый ряд динамики содержит указания о тех моментах либо периодах времени, к которым относятся уровни.

При подведении итогов статистического наблюдения получают абсолютные показатели двух видов. Одни из них характеризуют состояние явления на определенный момент времени: наличие на этот момент каких-либо единиц совокупности или наличие того или иного объема признака. К таким показателям относится численность населения, парк автомобилей, жилищный фонд, товарные запасы и т. д. Величину таких показателей можно определить непосредственно только по состоянию на тот или иной момент времени, а потому эти показатели и соответствующие ряды динамики и называются моментными.

Другие показатели характеризуют итоги какого-либо процесса за определенный период (интервал) времени (сутки, месяц, квартал, год и т. п.). Такими показателями являются, например, число родившихся, количество произведенной продукции, ввод в действие жилых домов, фонд заработной платы и др. Величину этих показателей можно подсчитать только за какой-нибудь интервал (период) времени, поэтому такие показатели и ряды их значений называются интервальными.

В моментном динамическом ряду одни и те же единицы совокупности обычно входят в состав нескольких уровней, поэтому суммирование уровней моментного ряда динамики само по себе не имеет смысла, так как получающиеся при этом итоги лишены самостоятельной экономической значимости.

Выше говорилось о рядах динамики абсолютных величин, являющихся исходными, первичными. Наряду с ними могут быть построены ряды динамики, уровни которых являются относительными и средними величинами. Они также могут быть либо моментными, либо интервальными. В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла, так как относительные и средние величины являются производными и исчисляются путем деления других величин.

При построении и перед анализом ряда динамики нужно прежде всего обратить внимание на то, чтобы уровни ряда были сопоставимы между собой, так как только в этом случае динамический ряд будет правильно отражать процесс развития явления. Сопоставимость уровней ряда динамики – это важнейшее условие обоснованности и правильности выводов, полученных в результате анализа этого ряда. При построении динамического ряда надо иметь в виду, что ряд может охватывать большой период времени, в течение которого могли произойти изменения, нарушающие сопоставимость (территориальные изменения, изменения круга охвата объектов, методологии расчетов и т. д.).

При изучении динамики общественных явлений статистика решает следующие задачи:

· измеряет абсолютную и относительную скорость роста либо снижения уровня за отдельные промежутки времени;

· дает обобщающие характеристики уровня и скорости его изменения за тот или иной период;

· выявляет и численно характеризует основные тенденции развития явлений на отдельных этапах;

· дает сравнительную числовую характеристику развития данного явления в разных регионах или на разных этапах;

· выявляет факторы, обусловливающие изменение изучаемого явления во времени;

· делает прогнозы развития явления в будущем.

Структура временных рядов.

В общем случае временной ряд можно разделить на составляющие его компоненты:

Основная компонента это тренд. (u)

Следующая компонента – сезонная. (s)

Циклическая компонента

Нерегулярная (случайная) компонента. (e)

Под трендом понимается устойчивое систематическое изменение процесса в течении продолжительного периода времени. На финансовых рынках различают тренд трех видов:

Возрастающий (бычий) тренд

Ниспадающий (медвежий) тренд

Боковой тренд (колебания происходят вокруг какого то среднего значения)

Для определения направленности используют слово тенденция. Это более общая характеристика, чем тренд. Тенденция среднего текущего значения является трендом.

Наряду с долговременными тенденциями во временных рядах экономических процессов часто наблюдаются более или менее регулярные колебания. Если такие колебания носят строго периодический характер и завершаются в течение одного года, то их называют сезонными колебаниями. Основной причиной, вызывающей сезонные колебания, является изменение природно-климатических условий в течение года. Сезонность также вызывают праздники, а также так называемые календарные эффекты, т.е. окончания кварталов, полугодий и т.д.

Сезонность оказывает негативное воздействие на экономические процессы, т.к. она приводит к аритмии производственных процессов.

Циклические колебания. Если период колебания составляет несколько лет, либо период колебания меньше года, то говорят о присутствии в процессе циклической компоненты. Для анализа процессов длительных колебаний нужны исходные данные за 100 лет и более.

Случайная компонента образуется из-за воздействия на экономический процесс случайных субъективных факторов. Если из исходного временного ряда правильно выделены систематические компоненты, то оставшаяся часть временного ряда и представляет собой случайные или нерегулярные компоненты. Временной ряд, составленный из значений случайной компоненты должен соответствовать ряду гипотез:

Его математическое ожидание должно приблизительно равняться нулю

Значения остаточной компоненты должны быть независимы друг от друга.

Совокупность значений остаточной компоненты должна подчиняться нормальному закону распределения.

Характеристики кривых роста

Удобным средством описания одномерных временных рядов является их выравнивание с помощью тех или иных функций времени (кривых роста). Кривая роста позволяет получить выравненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой.

Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы:

1) выбор одной или нескольких кривых, форма которых соответствует характеру изменения временного ряда;

2) оценка параметров выбранных кривых;

3) проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой роста;

4) расчет точечного интервального прогнозов.

В настоящее время в литературе описано несколько десятков кривых роста, многие из которых широко применяются для выравнивания экономических временных рядов.

Кривые роста условно могут быть разделены на три класса в зависимости от того, какой тип динамики развития они хорошо описывают.

К I типу относятся функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста. Эти условия справедливы для многих экономических показателей, например, для большинства натуральных показателей промышленного производства.

Ко II классу относятся кривые, описывающие процесс, который имеет предел роста в исследуемом периоде. С такими процессами часто сталкиваются в демографии, при изучении потребностей в товарах и услугах (в расчете на душу населения), при исследовании эффективности использования ресурсов и т.д. Примерами показателей, для которых могут быть указаны пределы роста, являются среднедушевое потребление определенных продуктов питания, расход удобрений на единицу площади ит.п.

Функции, относящиеся ко II классу, называются кривыми насыщения. Если кривые насыщения имеют точки перегиба, то они относятся к III типу кривых роста к S-образным кривым.

Эти кривые описывают как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): один с ускорением развития, другой - с замедлением.

S-образные кривые находят применение в демографических исследованиях, в страховых расчетах, при решении задач прогнозирования научно-технического прогресса, при определении спроса на новый вид продукции.

Вопрос о выборе кривой является основным при выравнивании ряда.

Группа кривых роста: Полиномы (многочлены) Экспоненциальные кривые S-образные кривые

Полиномы:

Полиномы первого порядка:

Yt=a_o+a₁t

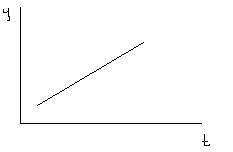
Ut=Yt-Yt-1=a₁

Скорость постоянная.

Полином второго порядка:

Yt=a_o+a₁t+ a₂t²

Прирост Ut= Yt-Yt-₁= a₁- a₂t+2a₂t

Анализируя формулу для вычисления приростов можно отметить 2 особенности:

- Вычислением прироста полином более высокого порядка можно привести к полиному более низкого порядка.

- В правых частях формул для вычисления приростов отсутствует значение самой функции, т.е. приросты зависят только от времени. С экономической точки зрения это означает следующее: если дальнейшее развитие исследуемого процесса не зависит от уже достигнутого им уровня, то хорошее описание такого процесса можно получить с использованием полинома какого либо порядка.

Экспоненциальные кривые:

Их использование в отличие от полиномов наоборот предполагает, что дальнейшее развитие процесса зависит от уже достигнутого уровня.

Простая экспонента:

Y=ab^t

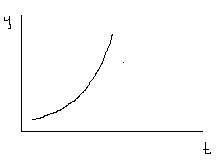
logYt=log a + t log b= a’ + b’t

Для процессов, соответствующих простой экспоненте, отношение прироста к ординате (или к функции) для каждого момента времени постоянно и равно параметру b.

Модифицированная экспонента.

Y=k+ab^t

K – асимптота, или предел насыщения, к которому стремится экспонента.

Для процессов, следующих по модифицированной экспоненте последовательное отношение приростов является постоянной величиной и равно параметру b.

S-образные кривые:

- Кривая Гомпертца

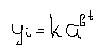
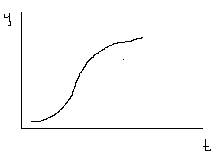
log (Ut/Yt) – линейно изменяется. (логарифм отношения прироста к функции)

- Логистическая кривая

Для логистической крвой изменяется логарифм отношения прироста к квадрату функции.

Все S-образные кривые имеют точку перегиба, до которой приросты положительны, после – отрицательны. Для логистической кривой нижняя и верхняя ветвь ее графического изображения симметричны относительно точки перегиба.

15 Производится с помощью метода наименьших квадратов.

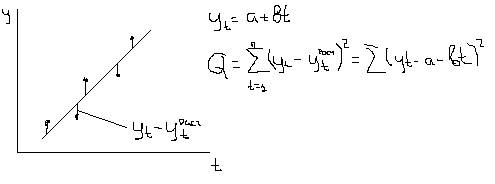
Q необходимо минимизировать.

Для этого берем частные производные по параметру a и b, приравниваем к нулю и вычисляем.

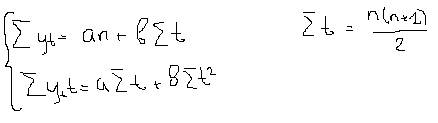
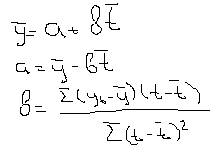
Это не подлинные параметры, а их оценки. Эти оценки обладают тремя свойствами:

1. Несмещенности

2. Состоятельности

3. Эффективности

Несмещенность означает, что математическое ожидание оценок параметра равно их истинному значению.

Состоятельность означает, что дисперсия оценок параметров стремиться к нулю при t стремящемся к бесконечности.

Эффективность означает, что оценки, вычисленные по методу наименьших квадратов имеют минимальную дисперсию по сравнению с оценками, полученными любым другим способом.

Поэтому при вычислении параметров уравнений кривых роста в первую очередь стараются использовать метод наименьших квадратов.

Метод наименьших квадратов можно использовать для вычисления параметров тех функций, в которых функция линейна относительно параметра.

Оценка параметров полинома второго порядка.

Поскольку функция линейна относительно параметра, можно применить метод наименьших квадратов, взяв три производных по трем параметрам и решив систему из трех уравнений.

Вычисление параметров простой экспоненты:

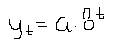
Т.к. свойство линейности относительно параметров не выполняется, то исходные уравнения путем различных преобразований стараются привести к линейному виду. Перевод уравнения из нелинейного в линейное называется линеализацией.

В данном случае процедура линеализации заключается в логарифмировании.

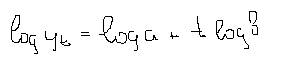
После решения системы уравнений, осуществляется потенцирование (обратный переход).

15Наиболее простой метод – визуальный, опирающийся на графическое изображение временных рядов. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если тенденция на графике просматривается недостаточно четко, то проводят преобразование исходного ряда. В литературе описан также метод последовательных разностей (помогает в выборе кривых параболического типа).

Этот метод применяют при выполнении следующих предположений:

1. уровни ряда могут быть представлены в виде суммы трендовой составляющей и случайной компоненты, подчиненной закону нормального распределения с математическим ожиданием, равным нулю и постоянной дисперсией; метод последующих разностей предполагает вычисление первых, вторых и т.д. разностей уровней ряда:

Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей принимается за степень выравнивающего полинома.
Этот прием можно использовать для преобразования временного ряда.
В отдельных случаях используют метод характеристик прироста. Процедура выбора кривых роста с использованием этого метода включает:

1) выравнивание ряда по скользящей средней;

2) определение средних приростов;

3) вычисление производных характеристик прироста

Для многих видов кривых были найдены такие преобразования приростов, которые линейно изменялись относительно t или были постоянны. В связи с этим исследование рядов характеристик приростов часто оказывает существенную помощь при определении законов развития исходных временных рядов.

Данный метод является более универсальным по сравнению с методом последовательных разностей.

Однако, чаще всего на практике к выбору формы кривой подходят исходя из значений критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровня от расчетных, получаемых выравниванием. Из рассматриваемых кривых предпочтение будет отдано той, которой соответствует минимальное значение критерия, т.к. чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений.
Используя этот подход, следует иметь в виду ряд моментов. Во-первых, к ряду, состоящему из m точек можно подобрать многочлен степени (m-1), проходящий через все m точек. Кроме того, существует множество многочленов более высоких степеней, также проходящих через все эти точки. Для этих многочленов значение критерия будет равно 0, однако, очевидно, что такая кривая не слишком пригодна как для выделения тенденции, так и для целей прогнозирования.

Также следует учитывать, что за счет роста сложности кривой можно увеличить точность описания тренда в прошлом, однако доверительные интервалы при прогнозировании будут существенно шире, чем у более простых кривых при одинаковом периоде упреждения, например, за счет большего числа параметров.

Таким образом, использование этого подхода должно проходить в два этапа. На первом происходит ограничение приемлемых функций, исходя из содержательного анализа задачи. На втором - осуществляется расчет значений критерия и выбор на его основе наиболее подходящей кривой роста.

В заключение отметим, что нет “жестких” рекомендаций для выбора кривых роста. Особенно осторожно следует подходить к решению этой задачи при использовании полученной функции для экстраполирования найденных закономерностей в будущее. Применение кривых роста должно базироваться на предположении о сохранении выявленной тенденции в прогнозируемом периоде.

Для многих процессов в экономике характерно наличие связи между значениями исследуемого показателя в предпро- гнозном и прогнозном периодах. Зависимость от времени проявляется в данном случае через характеристики внутренней структуры процесса в предшествующем периоде.

Уравнение, выражающее величину переменной yt в момент t через значения этой переменной в моменты (t -\),(t ~2),...,(t-р), называется уравнением авторегрессии. В линейной форме уравнение имеет вид:

Уг = «1^-1 + «2^-2 + • • • + aPyt-P + et> (4-24)

где st - случайная составляющая с нулевым математическим ожиданием и дисперсией сг? .

Применение авторегрессионных моделей основано на предварительном экономическом анализе, когда известно, что изучаемый процесс в значительной степени зависит от его развития в прошлые периоды. В некоторых случаях они используются для нахождения простого преобразования, приводящего к последовательности независимых случайных величин.

Существует другое определение авторегрессионной модели: модель стационарного процесса, выражающего значение показателя в виде линейной комбинации конечного числа предшествующих значений этого показателя и аддитивной случайной составляющей.

В процессе анализа реальных экономических явлений понятие стационарности может быть лишь удобной абстракцией для применения статистических моделей.

Количество уровней, включенных в правую часть уравнения авторегрессии, определяет порядок уравнения.

Для предварительного изучения особенностей автокорреляционного взаимодействия элементов ряда целесообразно проводить графический анализ исходных данных путем нанесения на координатные поля пар значений (У,,У,-МУ{>У{-2\->(У,,У,-Р)- Интервалы времени (t,i -k),k = 1,2,3,...,р, характеризующие удаленность сопоставляемых уровней ряда друг от друга, называются периодом запаздывания. Он показывает, через какой промежуток времени изменение переменной yt_k окажет воздей- ствие на yt. Изучение графических построений для различных к позволяет приближенно оценить направление и силу связи между близлежащими членами ряда.

Для оценки тесноты связи используется коэффициент автокорреляции, определяемый по формуле:

ск

г к=-*-, где

со

2 п-к ^ п

П t=1 п t=l

Определив гк для нескольких интервалов запаздывания в диапазоне 1 < к < п / 4 , можно получить так называемую автокорреляционную функцию, показывающую, как изменяется коэффициент автокорреляции по мере увеличения расстояния между сопоставляемыми уровнями временного ряда.

Автокорреляционная функция характеризуется тенденцией к затуханию колебаний, т.е. уменьшению абсолютной величины коэффициента. Вследствие этого для ее анализа используются такие характеристики, как период колебаний, частота колебаний, амплитуда колебаний, фаза, т.е угловая величина отклонения автокорреляционной функции от нулевого состояния.

Оценка параметров уравнений авторегрессии выполняется методом наименьших квадратов. Прогнозирование на основе авторегрессионной модели представляет многоэтапную процедуру, каждая стадия которой позволяет определить величину показателя на очередной единичный отрезок времени.

В качестве простейшего критерия адекватности уравнения авторегрессии исходному временному ряду может использоваться показатель абсолютного среднего отклонения, определяемый по формуле:

Z к-яI

= . , . (4.25)

n-p-l + l

Сферой применения моделей авторегрессии является моделирование спроса на предметы текущего потребления, изменение складских запасов и другие составляющие логистических процессов.

Задачи, функции и принципы прогнозирования

Экономическое прогнозирование призвано решать двуединую задачу: с одной стороны, давать объективную научно обоснованную картину будущего, опираясь на процессы сегодняшнего дня, а с другой - выбирать направление деятельности и политики современности с учетом прогнозных оценок. Наряду с этим важной задачей прогнозирования можно назвать выявление в настоящем тех факторов, которые будут оказывать свое влияние на исследуемый процесс в будущем.

Главная функция прогнозирования состоит в проведении научного анализа социально-экономических процессов и тенденций, а также в предвидении новых экономических ситуаций и выявлении узловых экономических проблем. Основные функции прогнозирования состоят также в исследовании объективных связей социально-экономических явлений и процессов в конкретных условиях, на определенном этапе развития экономики и общества, в оценке объекта прогнозирования, в выявлении возможных альтернатив развития экономики в перспективе, в принятии оптимальных решений.

Принципы прогнозирования меняются в зависимости от экономических условий, которые существуют на том или ином историческом этапе развития общества. В частности, со сменой социально-экономического строя в нашей стране ушли такие принципы, как партийность прогнозирования, принцип сочетания политики и экономики, принцип директивности планирования.

В рыночных условиях среди основных принципов, на которых базируется процесс прогнозирования, можно выделить следующие:

1) научная обоснованность прогноза (разработка с помощью научных методов, с учетом закономерности развития природы, общества и мышления);

2) непрерывность прогнозирования (прогноз должен постоянно корректироваться с учетом изменения ситуации в стране, экономике);

3) сочетание перспективного и текущего прогнозирования (данные виды прогнозирования осуществляются во взаимосвязи, но приоритет отдается перспективному прогнозированию);

4) согласованность