Статистико-экономический анализ уровней доходов и расходов населения
Первый раздел курсового проекта должен охарактеризовать понятие и методику расчета денежных доходов и расходов населения, индексов их изменения, баланса денежных доходов и расходов.
Второй раздел проекта будет включать: расчет аналитических показателей динамики денежного дохода и расхода, изучение их структуры за последние три года; выявление тенденции изменения и факторов его обусловивших. При этом должно проводиться сопоставление величины денежных доходов и расходов.
За последний год для более детального анализа явления может быть проведена группировка регионов по среднему уровню доходов или расходов населения.
В качестве факторов изменения доходов и расходов населения могут быть взяты: цены на промышленные товары, цены на продукты питания и др.
Статистико-экономический анализ макроэкономических показателей
Первый раздел курсового проекта должен включать описание сущности системы национальных счетов, принципов построения, методики расчетов макроэкономических показателей. В качестве исследуемого показателя может быть выбран один из макроэкономических показателей: валовая добавленная стоимость, валовой внутренний продукт, валовая прибыль экономики, валовой национальный доход и др.
Во втором разделе проекта необходимо провести расчет аналитических и средних показателей его динамики; выявить тенденцию изменения и факторы, его обусловившие. При использовании корреляционно-регрессионного анализа для получения более адекватных результатов, рекомендуется в качестве зависимой и независимых переменных использовать относительные показатели, например, валовой национальный доход в расчете на душу населения. В качестве факторов могут быть использованы индексы объема производства, индексы цен, величина экспорта и импорта и др.
Библиографический список
1.Рафикова Н.Т. Статистика. Уфа: Издательство БГАУ, 2003.-275 с.
2.Статисика/ Под ред.Харченко Л.П., Ионин Л.П.,Долженкова В.Г. - М.: ИНФРА-М, 2006.-250с.
3. Экономическая статистика / Под ред. Яковлева А.В.-М.: ИНФРА-М, 2005.-220с
4. Российский статистический ежегодник .2005.Стат.сб./ Росстат.-М, 2006.-819с.
ПРИЛОЖЕНИЕ А
Таблица А1 Формулы расчета показателей динамики
| Показатели | Способы расчета | |
| базисный | цепной | |
| Абсолютный прирост, ц | 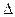 б = Уi – У1 б = Уi – У1 | 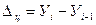 |
| Средний абсолютный прирост, ц | 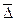 б= б= 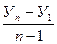 | 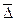 ц = ц = 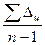 |
| Темп роста, % | 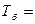 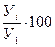 | 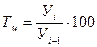 |
| Средний темп роста, % | 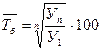 | 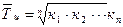 |
| Темп прироста, % | 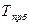 = = 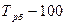 | 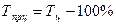 |
| Средний темп прироста, % | 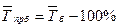 | 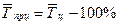 |
| Абсолютное содержание 1% прироста, ц | - | 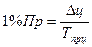 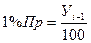 |
Результаты расчета должны быть представлены в виде таблицы А1
Таблица А1 Показатели динамики ….
| Годы | Уi | Абсолютный прирост | Темп роста,% | Темп прироста,% | Абсолютное содержание одного процента прироста | |||
| базисный | цепной | базисный | цепной | базисный | цепной | |||
| - | - | - | - | - | - | - | ||
| Итого | - | |||||||
| В среднем | - |
Приложение Б
Выявление и описание основной тенденции (тренда) динамического ряда осуществляется следующими методами:
- укрупнения интервала динамического ряда,
- методом скользящих средних,
- методом аналитического выравнивания.
Метод укрупнения интервала динамического ряда. Ряд динамики разделяют на некоторое число равных интервалов (например, 3 года) и рассчитывают средние уровни по укрупненным интервалам. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).
Метод скользящих средних. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих, при этом каждый раз смещаясь на один уровень.
Метод аналитического выравнивания. Аналитическое выравнивание осуществляется с применением метода наименьших квадратов. В основе, которого лежит требование минимизации суммы квадратов отклонений фактических уровней от выровненных значений, исчисленных по определенной функции, например прямой 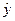 t=а+bt. Для определения параметров уравнения а и b в соответствии с требованиями данного метода составляется система из двух нормальных уравнений:
t=а+bt. Для определения параметров уравнения а и b в соответствии с требованиями данного метода составляется система из двух нормальных уравнений:
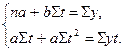
Для упрощения расчетов применяется способ отсчета от условного начала, где значения дат заменено отклонениями (t) от даты, занимающей центральное место в динамическом ряду (t=0). В следствии того, что 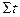 =0, система уравнений упрощается и
=0, система уравнений упрощается и 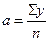 ,
, 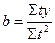 .
.
Аналитическое выравнивание может быть произведено с использованием ППП Excel:
1.Постройте таблицу Б1, включающую расчетные показатели для определения параметров уравнения тренда.
Определите расчетные показатели с применением «Мастера функций» ( СУММ, СРЗНАЧ.и т.д.) или вводом функции в соответствующую ячейку с клавиатуры. После расчета показателей, подставьте их в формулы определения параметров уравнения.
Таблица Б1Аналитическое выравнивание результативного показателя с 1999 по 2005 г.
| Год | у | t | уt | t2 | 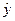 |
| у1 | -3 | ||||
| у2 | -2 | ||||
| у3 | -1 | ||||
| у4 | |||||
| у5 | |||||
| у6 | |||||
| у7 | |||||
| Итого | ∑у | ∑ уt | ∑ t2 |
Коэффициент b покажет среднегодовое увеличение (уменьшение) у . Параметр a будет представлять собой значение выровненного уровня ряда для центрального в динамическом ряду года, принятого за условное начало отсчета.
Сделать точечный прогноз на перспективу можно путем подстановки в полученное уравнение значений отклонений от центрального года для прогнозируемых периодов, например для 2006г. это значение 4. Затем можно рассчитать доверительный прогноз на будущий год, с учетом доверительной ошибки прогноза.
2.Получить в ППП Excel уравнение тренда ряда динамики можно также с применением «Мастера диаграмм». Построив диаграмму по фактическим уровням ряда и выбрав пункт меню «Диаграмма» / «Добавить линию тренда», необходимо также указать в пункте «Параметры» вывод уравнения тренда и величины достоверности аппроксимации R2. В дальнейшем используя коэффициент R2 произвести отбор функции тренда наиболее адекватно отражающей фактическую тенденцию изменения показателя во времени.
При этом надо учесть, что в рассчитанном программой уравнении тренда
у= bх+a, х.будет представлять порядковый номер года и изменяться от 1 до n (в нашем примере от 1 до 7). Следовательно, при определении прогнозного уровня ряда в 2006г. необходимо будет подставлять значение х=8.
Приложение В
Методика проведения парной линейной регрессии изучаемого социально-экономического показателя.
Таблица В1 Исходные данные
| Год | Изучаемый показатель (У) | Фактор (Х) |
| … | … | … |
Для исключения автокорреляции остатков для дальнейшего корреляционно-регрессионного анализа должны использоваться отклонения от тренда или цепные абсолютные приросты: ∆ц у=Уi- Уi-1 , ∆ц х=Хi- Хi-1.
Таблица В2 Исходные данные для корреляционно-регрессионного анализа
| Год | ∆ц у | ∆ц х |
| … | … | … |
В ППП Excel ввести таблицу с исходными данными. Выбрать пункт меню «Сервис»/ «Анализ данных» / выбрать «корреляция». Полученный результат в виде матрицы коэффициентов парной корреляции представлен в таблице В3.
Таблица В3 Матрица коэффициентов парной корреляции
| У | Х | |
| У | ||
| Х | rху |
Коэффициент парной корреляции до │0,3│будет свидетельствовать о несущественной степени связи между переменными, от │0,3 │до │0,5│- о слабой, от │0,5│ до│0,7│ – об умеренной, и свыше │0,7│ - о сильной.
Следующим этапом будет проведение регрессионного анализа. В пункте «Сервис»/ «Анализ данных» / выбрать «регрессия», затем в данном диалоговом окне указать диапазон результативного (У) и факторного показателей (Х), отметить значком «v» строки «вывод остатков» и «график остатков». Пакет анализа выведет итоговые результаты расчетов представленные в таблицах В4,В5,В6,В7.
Таблица В4 Регрессионная статистика
| Множественный R | |
| R-квадрат | |
| Нормированный R-квадрат | |
| Стандартная ошибка | |
| Наблюдения |
Коэффициент детерминации r2 показывает, сколько процентов изменения прироста У обусловлено вариацией цепного прироста Х.
Оценка значимости уравнения регрессии в целом приводиться согласно дисперсионного анализа по F –критерию Фишера, приведенному в таблице В5. Если Fфакт>F табл ( α=0,05, к1=m=1, к2 =n-m-1), то уравнение является статистически значимым, если F факт < F табл, то не значимым.
Таблица В5 Дисперсионный анализ
| df | SS | MS | F | Значимость F | |
| Регрессия | |||||
| Остаток | |||||
| Итого |
Таблица В6 Основные характеристики параметров регрессионного уравнения.
| Коэффи-циенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | ||||||
| Х |
Коэффициент регрессии показывает, на сколько произойдет увеличение (уменьшение) ежегодного прироста У от своего среднего значения при увеличение прироста Х на 1.
Проверка значимости параметров уравнения регрессии проводиться на основе t-критерия Стьюдента (t –статистика). Так если tфакт> tтабл, то параметр уравнения является статистически значим, а если не tфакт< tтабл (α=0,05, df =n-m-1), то незначим.
В таблице В7 приводятся отклонения фактических данных результативного показателя от предсказанных, согласно уравнению прямой, после подстановки в него фактических значений Х.
Таблица В7 Остатки
| Наблюдение | Предсказанный У | Остатки |
| … | … | … |
Если с точки зрения целесообразности лучшем для результативного показателя является его повышение, то о резервах роста будут свидетельствовать отрицательные остатки по каждому отдельному наблюдению, если уменьшение, то положительные.
