Пример расчета газового цикла

Дано: цикл, отнесенный к 1 кг воздуха в координатах p-v и состоящий из четырех процессов: адиабатного 1-2, изохорного 2-3, политропного 3-4, изобарного 4-1; некоторые параметры точек цикла (рис. 1.9.)

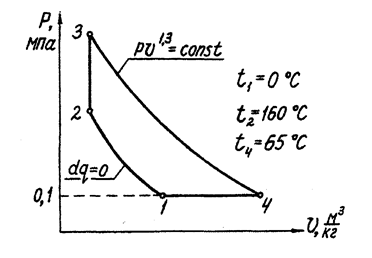Рис. 1.9. Газовый цикл в p-v – координатах.

1.Определение параметров p, T, v, u, h для основных точек цикла

а). Для точки 1 дано: p₁ = 0,1 MΠa, t₁ = 0°C.

Определим v₁, u₁, h_1.

Удельный объем

v₁ = 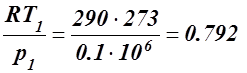м³/кг.

Условно принимаем, что внутренняя энергия и энтальпия равны нулю при t = 0°C, тогда

u₁ = C_v · t₁ = 0,

h₁ = C_p · t₁ = 0.

б). Для точки 2 дано: t₂ = 160°C. Определим v₂, p₂, u₂, h₂.

Для нахождения v₂ используем уравнение адиабаты в v,T координатах

T · v 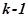= const,

где

k = ,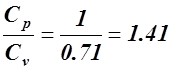

или

,

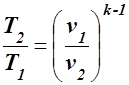откуда

v₂ = v₁ 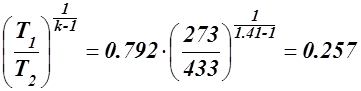м³/кг.

Для определения давления p₂ используем уравнение состояния p₂ v₂ = RT₂, откуда

p₂ = 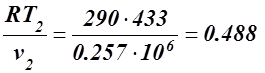МПа.

Внутренняя энергия u₂ = C_v · t₂ = 0.71 · 160 = 114 кДж/кг,

энтальпия h₂ = C_p· t₂ = 1.0 · 160 = 160 кДж/кг.

в). Для точки 4 дано: t₄ = 65°C; p₄ = p₁ = 0.1 MΠa.

Определим v₄, u₄, h₄.

Для определения v₄ используем соотношение параметров изобарного процесса 4 – 1

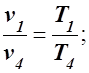v₄ = 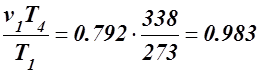м³/кг.

Внутренняя энергия u₄ = C_v · t₄ = 0.71 · 65 = 46.15 кДж/кг,

энтальпия h₄ = C_p · t₄ = 1.0 · 65 = 65 кДж/кг.

г). Для точки 3 дано: v₃ = v₂ = 0.257 м³/кг.

Определим T₃ , p₃ , u₃ , h₃ .

Для нахождения T₃ используем уравнение политропы

,

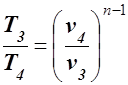T₃ = T₄ ·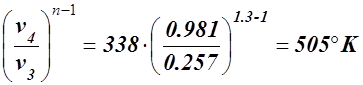

Для определения p₃ используем уравнение состояния

p₃ = 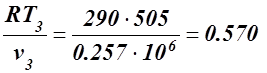МПа.

Внутренняя энергия u₃ = C_v · t₃ = 0.71 · 233 = 165.43 кДж/кг,

энтальпия h₃ = C_p · t₃ = 1.0 · 233 = 233 кДж/кг.

Таблица 1.2.

Параметры Точки	р, МПа	v, м³/кг	Т, К	и, кДж/кг	h, кДж/кг
	0,100	0,792
	0,488	0,257
	0,570	0,257		165,43
	0,100	0,981		46,15

Результаты расчетов помещаем в табл. 1.2.

2. Для каждого процесса, входящего в состав цикла, найдем n, c, Δu, Δh, Δs, q, l, a, b.

Определим перечисленные величины

а). Для адиабатного процесса 1 – 2 при C_p = const, C_v = const

n = k =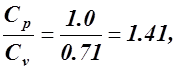

с = 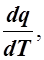так как для адиабаты dq = 0, то c = 0.

Изменение внутренней энергии Δu_1-2 = u₂ - u₁ = 144 – 0 = 144 кДж/кг.

Изменение энтальпии Δh_1-2 = h₂ - h₁ = 160 – 0 = 160 кДж/кг.

Изменение энтропии Δs_1-2 = s₂ - s₁ = 0, так как для обратимой адиабаты

s = const. Адиабатный процесс протекает без теплообмена с окружающей средой, поэтому q = 0.

Работу процесса определим из уравнения первого закона термодинамики q=Δu +l, т.к. q = 0, тоl = - Δu = - 114 кДж/кг. Величины a,b не определяем, т.к. теплота процесса q = 0.

б). Для изохорного процесса 2 – 3 показатель политропы n = ±∞, теплоемкость C_v = 0.71 кДж/кг·К. Изменение внутренней энергии

Δu_2-3 = u₃ - u₂ = 165.43 – 114 = 51.43 кДж/кг.

Изменение энтальпии и энтропии

Δh_2-3 = h₃ - h₂ = 233 – 160 = 73 кДж/кг;

Δs_2-3 = s₃ - s₂ = C_v ln 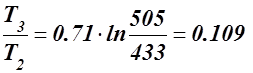кДж/кг·К.

Для изохорного процесса l = 0, поэтому для этого процесса из уравнения первого закона термодинамики следует

q = Δu = u₃ - u₂ = 51.43 кДж/кг.

a =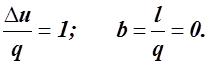

в). Для политропного процесса 3 – 4 при показателе политропы n = 1.3

C = C_v 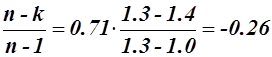кДж/кг·К;

Δu_3-4 = u₄ - u₃ = 46.15 - 165.43 = - 119.28 кДж/кг;

Δh_3-4 = h₄ - h₃ = 65 – 233 = - 168 кДж/кг;

Δs_3-4 = s₄ - s₃ = C_v ln 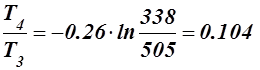кДж/кг·К;

q = c(T₄ - T₃) = - 0.26(338 - 505) = 43.42 кДж/кг.