Расчёт фермы на вертикальную узловую нагрузку

· Схемы приложения постоянной и снеговой нагрузок совпадают, поэтому целесообразно рассчитать ферму в общем виде, то есть на действие узловых сил Р. Расчёт достаточно провести только для половины фермы, поскольку нагрузка и конструкция симметричны.

· При проведении расчёта воспользуемся графическим методом. Этот метод несложен по своей сути, но требует определённого навыка в использовании. Кроме того, необходимо обращать внимание на точность построений.

· Диаграммы Кремоны для ферм пролётом 24 и 30 м представлены на рис. 5.5, а и б. В таблицах 5.2.а и 5.2.б приводится сравнение результатов, полученных графическим и аналитическим способами.

Построение диаграммы Кремоны

· Построение диаграммы Кремоны состоит из четырёх этапов.

Формирование исходных данных

В масштабе вычерчивается геометрическая схема фермы, на которой показываются приложенные к ней усилия, включая опорные реакции.

Маркировка полей

Полем называется пространство на схеме фермы, ограниченное или внешними силами, или стержнями фермы (то есть внутренними усилиями). Ненагруженные стержни из рассмотрения можно исключить.

При обозначении внутренних усилий индексы будут соответствовать не номерам узлов начала и конца стержня, а номерам полей, которые разграничивают эти усилия. Например, N_А-1 – усилие в опорном раскосе; N_К-1 – усилие в крайней панели нижнего пояса.

Построение многоугольников внешних и внутренних сил

Каждому внутреннему усилию в ферме соответствует луч (отрезок) в многоугольнике сил на диаграмме Кремоны. При этом соблюдаются следующие правила:

1) Номера начала и конца отрезка соответствуют маркировке усилия.

2) Направление отрезка параллельно линии действия соответствующего ему усилия.

3) Длина отрезка равна численному значению усилия, выраженного в масштабе сил. В данном случае в качестве масштаба сил используется величина Р.

Многоугольник внешних сил строим, обходя контур фермы по часовой стрелке. При построении многоугольника внутренних сил начинаем с наиболее простого узла фермы, в котором только одна неизвестная точка. Обойдя этот узел по часовой стрелке, определяем неизвестную точку, затем переходим к другому узлу.

Неизвестные точки находятся в местах пересечения лучей, соответствующих стержням, сходящимся в одном узле. В результате построения длина отрезков в масштабе сил получается равной усилиям в соответствующих элементах.

Измерение отрезков и определение знаков

Правило знаков: если при обходе узла по часовой стрелке луч направлен к узлу, то стержень сжат, а если от узла – растянут.

Величина внутреннего усилия и его знак отмечаются на диаграмме.

монтажный стык

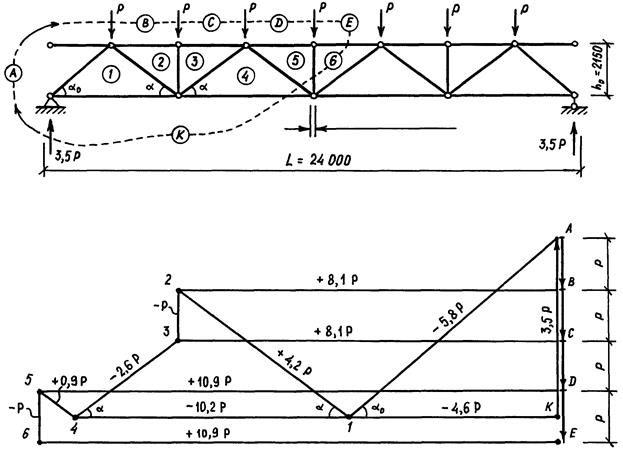
Рис. 5.5.а. Диаграмма Кремоны для фермы пролётом 24 м.

Таблица 5.2.а.

Усилия в элементах фермы пролётом 24 м

Элемент	Обозначение	Усилия в стержнях ´Р, при расчёте	Расхождение*
графическим методом	Аналитическим методом*
Верхний пояс	B-2; C-3	– 8,1	– 8,05
D-5; E-6	– 10,9	– 10,84
Нижний пояс	K-1	+ 4,6	+ 4,56
K-4	+ 10,2	+ 10,14	0,6 %
Сжатый раскос	A-1	– 5,8	– 5,75
3-4	– 2,6	– 2,58
Растянутый раскос	1-2	+ 4,2	+ 4,11	2,2 %
4-5	+ 0,9	+ 0,86
Стойка	2-3; 5-6	– 1,0	– 1,0
* - выполнять не обязательно

монтажный стык

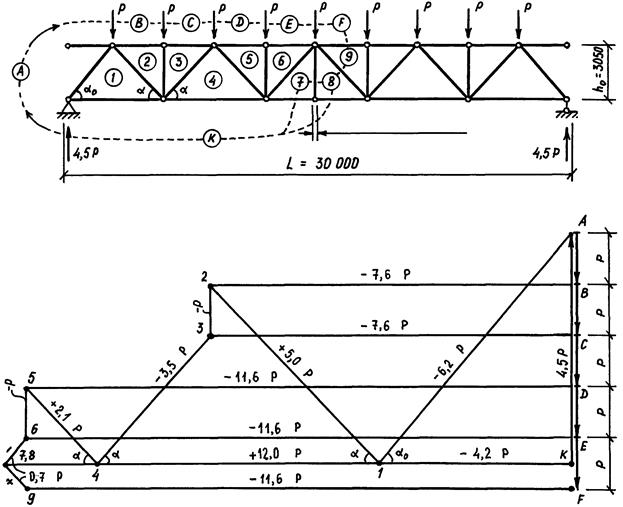
Рис. 5.5.б. Диаграмма Кремоны для фермы пролётом 30 м.

Таблица 5.2.б.

Усилия в элементах фермы пролётом 30 м

Элемент	Обозначение	Усилия в стержнях ´Р, при расчёте	Расхождение*
графическим методом	аналитическим методом*
Верхний пояс	B-2; C-3	– 7,6	– 7,57
D-5; E-6; F-9	– 11,6	– 11,51	0,8 %
Нижний пояс	K-1	+ 4,2	+ 4,13
K-4	+ 10,0	+ 10,03
K-7; K-8	+ 12,0	+ 12,0
Сжатый раскос	A-1	– 6,2	– 6,11
3-4	– 3,5	– 3,51
6-7; 8-9	– 0,7	– 0,70
Растянутый раскос	1-2	+ 5,0	+ 4,91
4-5	+ 2,1	+ 2,10
Стойка	2-3; 5-6	– 1,0	– 1,0
* - выполнять не обязательно

Расчёт фермы на действие горизонтальных нагрузок

Расчёт на действие распора рамы

· В расчётной схеме поперечной рамы ригель располагался на уровне нижнего пояса фермы, поэтому распор рамы Н приложен к нижнему поясу, и усилия от распора возникают только в элементах нижнего пояса. Допустимо считать, что усилия по длине пролёта распределяются линейно (см. рис. 5.3,б).