Задание точки, расположенной в различных углах (октантах) пространства

Для однозначного определения положения точки в пространстве проецирование выполняют на две и более плоскостей проекций.

На рис. 1.4 представлено проецирование точки на три взаимно перпендикулярных плоскости проекций. Плоскость П₁ располагают горизонтально и называют горизонтальной плоскостью проекций; П₂ – фронтальная плоскость проекций; П₃ –профильная плоскость проекций.

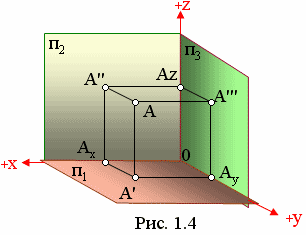
Как видно из рисунка, горизонтальная проекция точки (A') определяется координатами А_х и А_у; фронтальная (А'') – Ах и А_z; профильная (А''') - А_у и А_z.

Расстояние от точки до горизонтальной плоскости π₁ в пространстве определяется величиной отрезка [А A'], на чертеже - [А''А_х], то есть [А A'] = [А''А_х]. Эта величина дает представление о высоте расположения точки относительно горизонтальной плоскости.

Аналогично величина отрезка [А А''] в пространстве равна величине [A' А_х] на чертеже и дает представление о глубине расположения точки относительно фронтальной плоскости. Так же [А А'''] = [A' А_у] и = [А''А_z].

Таким образом, высоту точек измеряют на фронтальной плоскости. Глубину – на горизонтальной.

Плоскости проекций не ограничиваются только своими положительными направлениями, поэтому все пространство делится ими на восемь углов – восемь октантов. Нумерация октантов производится против хода часовой стрелки, начиная с первого, изображенного на рис. 1. 5 а.

Чтобы получить плоскую модель, надо горизонтальную и профильную плоскости проекций совместить с фронтальной путем вращения их вокруг осей.

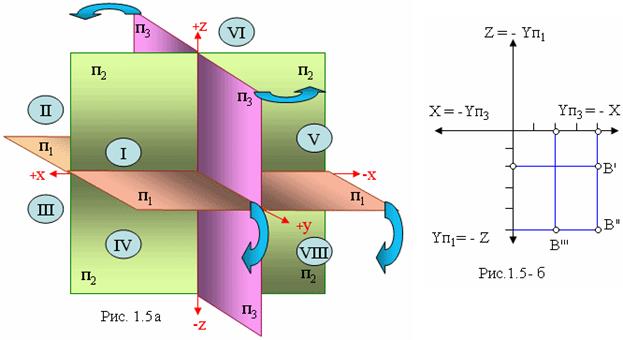
На рис. 1.5-б представлены совмещенные плоскости проекций, где отмечены как положительные, так и отрицательные направления по осям Х, У и Z.

Для построения проекций точек, расположенных в различных углах пространства, необходимо учитывать знаки координат этой точки (плюс или минус). На рис.1.5-б построена проекция точки В, заданная координатами: В_х = - 4; В_y = + 2; B_z = -5.

Теперь вы должны выполнить задачу 1 контрольной работы

Практическое занятие 1
Задание точки, расположенной в различных углах (октантах) пространства

Ранее было отмечено, что плоскости проекций не ограничиваются только своими положительными направлениями, поэтому все пространство делится ими на восемь углов – восемь октантов. Нумерация октантов производится против хода часовой стрелки, начиная с первого. Чтобы получить плоскую модель, надо горизонтальную и профильную плоскости проекций совместить с фронтальной путем вращения их вокруг осей (см. рис. 1.5 - а).

При построении проекций точки необходимо учитывать знаки значений координат точек (плюс или минус), как это выполнено на рис. 1.5 – б.

Вам предлагается согласно вашему варианту на чертежной бумаге построить проекции восьми точек и указать номер угла (октанта). Затем, для проверки правильности своих решений, вызвать Репетиционный тест «Задание точки» и сопоставить решения и ответы.

В качестве контрольного теста Вам будет предложено два типа задач:

1. Будет предложен чертеж одной точки. Надо определить, в каком октанте она расположена. Ответ выбрать из пяти предложенных вариантов.

2. Будет предложено пять чертежей точки. Надо выбрать правильный чертеж.

Репетиционный тест представляет собой компьютерную программу. В программе можно последовательно, не выходя из нее, построить проекции нескольких точек. Ее можно многократно вызывать.

Чтобы быстро определить октант, в котором расположена точка, надо мысленно построить «векторы знаков». Например, точка А задана координатами: Ах = -5; Ау = +3; Аz = -6. Построив цепь векторов знаков (см. рис.1): X = -; Y = +; Z = - , видим, что точка расположена в восьмом октанте.

В связи со сложностью использования в программе условных обозначений, принятых в некоторых учебниках начертательной геометрии, например, обозначение f_0β" и других, в программе могут использоваться иные обозначения: плоскости проекций могут быть обозначены как π₁ , π₂ …, соответственно вместо обозначений проекций точек А' ; А"приняты обозначения А₁, А₂.

В процессе решения задач подобного типа надо помнить, что горизонтальная проекция точек определяется значениями по оси Х и Yп1, то есть:
Горизонтальная - А₁ (Х; Yп1), фронтальная - А₂ (Х; Z), профильная - А₃ (Yп3; Z) (1)

Репетиционный тест: Тема 1.1.3. Задание точки

Рекомендации: при ответах на контрольные тесты имейте перед собой два – три листа чистой бумаги и ручку (карандаш). После вызова задачи первого типа заполните таблицу знаков:

	X	Y	Z	Октант
Точка A	-	+	-	VIII

Затем нарисуйте схему, или представьте ее мысленно в пространстве, подобную рис. 1 и Вы без труда укажите правильный ответ. Воспользоваться дополнительной литературой (шпаргалками) Вы вряд ли успеете.

В задачах второго типа надо определить местоположение третьей – недостающей проекции точки по двум заданным и выбрать чертеж с правильным ответом. Алгоритм решения тот же: установите знаки по осям (заполните таблицу) и согласно выражению (1) определите, где должна располагаться третья (недостающая на каждом чертеже) проекция точки. Выберите чертеж с правильным ответом.