Линейчатые поверхности. Принадлежность линии и точки к поверхности

Линейчатой называется поверхность, образующей которой является прямая линия.

В общем случае линейчатая поверхность однозначно определяется тремя направляющими линиями [8, стр. 142].

Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этойповерхности. Для задания поверхности достаточно иметь проекции направляющей линии и указать, как строится образующая прямая, проходящая через любую точку направляющей. Однако, для придания наглядности изображения, вычерчивают очерк, линии видимости и строят точки на поверхности.

Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некоторой кривой направляющей линии. Если направляющей линией является окружность, то поверхность называется наклонным или эллиптическим конусом.

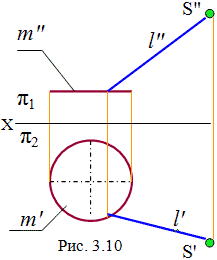
На рис. 3.10 представлены: направляющая окружность – m; неподвижная точка – S; прямолинейная образующая - l . Это первая часть определителя – геометрическая. Образующая движется по направляющей, оставаясь неподвижной в точке S. Описание закона движения является алгоритмической частью определителя. При этих условиях поверхность на чертеже считается заданной. Для придания наглядности, на рис. 3.11 построены очертания поверхности, линии видимости и промежуточная точка, принадлежащая поверхности.

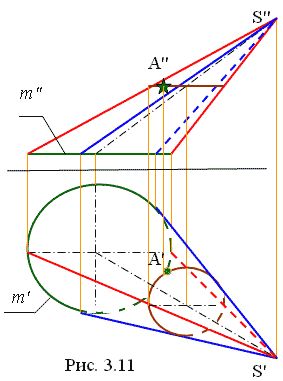
Построение точек, принадлежащих поверхности, осуществляется следующим образом. Пусть задана фронтальная проекция точки А (А"). На фронтальной плоскости она изображена как невидимая. Для построения ее горизонтальной проекции через точку задаем линию, принадлежащую поверхности. Этой линией будет окружность, так как линия задана параллельно основанию, а основанием является окружность. Центр окружности лежит на осевой линии поверхности. Проводим линию связи из центра окружности на горизонтальную плоскость до пересечения с горизонтальной осевой поверхности. Строим окружность, которой принадлежит точка А.. По линии связи отмечаем ее местоположение с учетом видимости для горизонтальной плоскости, где точка является видимой. Аналогичные построения выполняются для наклонного (эллиптического) цилиндра.

Тема 4

Позиционные задачи

Все задачи начертательной геометрии условно могут быть разделены на метрические и позиционные. К метрическим задачам относятся задачи на измерение линейных и угловых величин. Решение этих задач будет рассмотрено ниже.

К позиционным задачам относятся задачи на принадлежность и взаимное пересечение геометрических фигур. По существу решение позиционных задач сводится к нахождению точек одновременно принадлежащих двум или более фигурам. Задачи на определение принадлежности одной геометрической фигуры к другой частично уже рассмотрены:

o принадлежность точки к прямой (рис. 1.23) .

o принадлежность линии к поверхности. Рис. 3.9 ;

o принадлежность точки к поверхности. Рис. 3.11

Задачи на построение линий пересечения геометрических фигур условно можно разделить на три группы:

o пересечение плоскости с поверхностью;

o пересечение прямой линии с плоскостью и с поверхностью.

o взаимное пересечение поверхностей.

Решение всех типов позиционных задач на пересечение подчиняются общему алгоритму. На рис. 4.1 представлена поверхность полусферы и усеченного конуса. Для построения точек, одновременно принадлежащих этим поверхностям, воспользуемся общим алгоритмом.

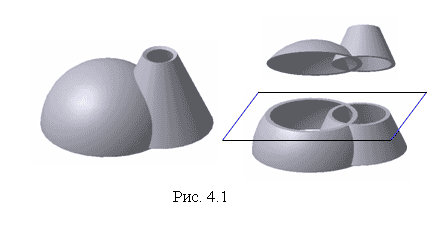
1. Вводится вспомогательная поверхность, в частном случае - плоскость. Эта вспомогательная поверхность назначается таким образом, чтобы она пересекла обе фигуры по простым для построения линиям - по прямым или по окружностям.

2. Строятся линии пересечения вспомогательной поверхности с каждой из заданных фигур.

3. Отмечаются точки взаимного пересечения построенных линий. Эти точки принадлежат обеим фигурам, следовательно, являются элементом пересечения фигур.

4. Соединяют точки в определенной последовательности и определяют видимость линии пересечения и фигур друг относительно друга.

Находить точки для построения линии взаимного пересечения фигур надо в определенной последовательности.

1. В первую очередь отмечают точки на контурных образующих или на ребрах, если поверхностигранные.

2. Находят экстремальные точки: наивысшую; наинизшую; самую левую; самую правую; самую ближнюю и самую дальнюю.

3. Отмечают точки на линиях среза (принадлежащие основаниям).

4. Если построенных точек недостаточно для выявления формы линии взаимного пересечения, строят ряд промежуточных (случайных) точек.