Порядок выполнения работы задания 6.1
Схема экспериментальной установки для выполнения задания изображена на рис. 6.7. Пучок параллельных когерентных лучей, испускаемых лазером 1, падает на щель 2. Регулируя щель микровинтом 3, можно ограничить фронт волны и вырезать лишь узкий плоский участок. В этом случае на экране 4, отстоящем достаточно далеко от щели, будет наблюдаться дифракционная картина. Измерение ширины главного максимума, расположенного в центре дифракционной картины (см. рис. 6.6.), производится при помощи линейки, при различных значениях ширины щели, регулируемой микрометрическим винтом.
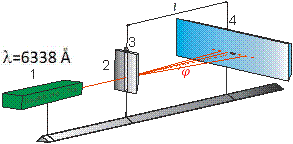
Рис. 6.6. Схема экспериментальной установки для исследования дифракции на щели: 1 - лазер; 2 - щель; 3 - микрометрический винт;
4 - экран;
1. Включить лазер.
2. Собрать схему экспериментальной установки (рис. 6.7)
3. При фиксированном расстоянии между щелью и экраном исследовать зависимость ширины главного дифракционного максимума от ширины щели.
4. Заполнить таблицу экспериментальных значений.
Таблица 6.1
| № п/п | Ширина щели, b, мм | Ширина главного дифракционного максимума, L, мм |
| … | ||
5. Построить график зависимости ширины главного дифракционного максимума L (мм) от ширины щели b (мм).
6. Сравнить полученный экспериментальный график с теоретической зависимостью ширины главного максимума от размеров щели в соответствии с формулой (3) и зависимостью I(sinj), представленной рис. 6.6.
Контрольные вопросы к заданию 6.1
1. В чем заключается принцип Гюйгенса - Френеля?
2. Как формулируются условия когерентности двух волн?
3. Чем отличается дифракции Френеля от дифракции Фраунгофера?
4. Как формулируется условие возникновения максимумов и минимумов при дифракции света на щели?
5. Как влияет ширина щели на дифракционную картину?
6. Как построить векторную диаграмму для определений амплитуды колебаний в случае дифракции от щели?
Задание 6.2. Определение постоянной
Дифракционной решетки
Приборы и принадлежности: источник света – He-Ne лазер (l=6328 Å); дифракционные решетки; экран с миллиметровым масштабом; измерительная линейка.
Цель задания: экспериментальное исследование распределения освещенности при дифракции света на дифракционной решетке, определение постоянной решетки.
Краткая теория
Дифракционной решеткой называется периодическая структура, состоящая из элементов, соизмеримых (в пределах нескольких порядков) с длиной волны. Кристаллы твердых тел представляют собой трехмерную пространственную дифракционную решетку, линейные элементы, расположенные на плоскости, могут образовать плоскую решетку, ряд точек — линейную.
Прозрачные плоские дифракционные решетки изготавливаются в виде пластин из какого-либо прозрачного материла, на который алмазным резцом наносят равно отстоящие друг от друга одинаковые штрихи. Ширина прозрачного промежутка а и непрозрачного b должна быть строго постоянной для каждой решетки. Их сумма а + b = d называется постоянной, или периодом решетки.
Принципиальная схема наблюдения дифракции на прозрачной решетке представлена на рис. 6.8.
Пусть на дифракционную решетку 1 перпендикулярно ее плоскости падает пучок параллельных когерентных лучей. Решетка вызывает дифракцию световых лучей, и в фокальной плоскости 3 линзы 2 образуется сложное дифракционное изображение.
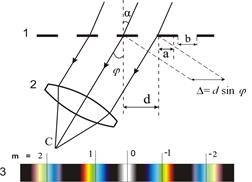
Рис. 6.8. Дифракция на дифракционной решетке
Каждая щель решетки дает дифракционную картину в полном соответствии с картиной, описанной в задании 6.1. При этом дифракционные максимумы и минимумы налагаются друг на друга. Однако теперь явление усложняется тем, что кроме дифракции от каждой щели будет происходить еще интерференция многих пучков, т. е. сложение колебаний, приходящих в данную точку от всех щелей. Если общее число щелей N, то интерферируют между собой N пучков.
Рассмотрим пучок параллельных лучей, дифрагировавших под углом j. Амплитуды колебаний, пришедших в точку С от всех щелей, будут одинаковы, обозначим через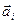 
. Разность хода D между лучами от каждой из двух соседних щелей, как видно из рис.6.7, равна
D = (а + b) sin j = d sin j. (6.4)
Этой разности хода соответствует разность фаз между соседними лучами от каждых двух соседних щелей, равная
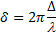. (6.5)
Суммарную амплитуду можно представить графически вектором замыкающей ломаной линии, образованной векторами амплитуд 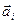. Очевидно, что вектор 
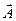достигает максимальной величины во всех случаях, когда векторы 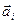расположены вдоль одной прямой (рис. 6.4, а). Это имеет место при d = ± 2kp, где k = 0,1,2… При этом длина вектора 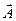равна сумме векторов амплитуд от всех щелей 
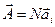. Освещенность прямо пропорциональна квадрату амплитуды. Следовательно, максимальная освещенность Imax будет равна
Imax = CN2a2 , (6.6)
где C - коэффициент пропорциональности.
Максимумы, соответствующие условию (6.6), называются главными.
Вектор 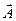становится равным 0, когда ломаная линия, образованная векторами 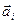, превращается в замкнутую линию (рис. 6.4, б), т. е. когда последний вектор 
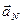направлен так же, как 
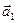, но последний составляет с осью ОХ угол Nd . Следовательно, вектор 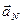будет параллелен оси ОХ при Nd = ± 2kp, где k = 1, 2, 3 …
Таким образом, получаем условие образования минимумов
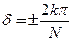. (6.7)
В минимумах освещенность Imin = 0. Нетрудно видеть, что между максимумами имеется N–1 минимум, а следовательно, еще N–2 максимума. Эти максимумы очень слабые и называются вторичными максимумами.
Приняв во внимание соотношение (6.4) и (6.5), получим, что главные максимумы возникают при значениях угла j, удовлетворяющих условию
d sin j = ± kl; k = 0,1,2. (6.8)
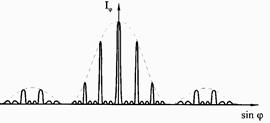
Рис. 6.9. Распределение освещенности при дифракции на дифракционной решетке состоящей из четырех щелей
Целое число k называют порядком спектра, выражение (6.8) - формулой дифракционной решетки. Минимумы возникают при значениях j, удовлетворяющих условию
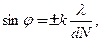k = 1,2,3… , (6.9)
кроме k = N, 2 N, 3 N...
Учитывая дифракцию от каждой щели и описанную ранее интерференцию от N щелей решетки, освещенность I в фокальной плоскости линзы 3 (рис. 6.8) получим в виде произведения I = I1I2, где I1 - освещенность, обусловленная дифракцией на каждой щели, I2 – освещенность, обусловленная интерференцией на решетке. На рис. 6.7 представлено истинное распределение освещенности при дифракции от четырех щелей.
Если на дифракционную решетку падает не монохроматический пучок лучей, то условия максимумов (6.7) и минимумов (6.9) будут справедливы для всех длин волн и в фокальной плоскости 3 линзы 2 (рис. 6.7) будет наблюдаться дифракционный спектр в виде смещенных максимумов для всех длин волн источника света.
Как показывает формула (6.8), в центре будет максимум нулевого порядка для всех длин волн l1, l2,…, ln . По обе стороны от этого максимума будут располагаться максимумы 1-го, 2-го и т.д. порядков, соответственно для всех длин волн l1, l2,…; при этом, чем короче длина волны, тем ближе расположен соответствующий максимум к центральному. Эта картина будет дифракционным изображением, полученным в результате ограничения светового пучка дифракционной решеткой. Следовательно, дифракционная решетка – прибор, разлагающий белый свет на составные части, с ее помощью получается дифракционный спектр. Формула (6.8) позволяет определить длину волны l, если известна постоянная решетки d и порядок максимума k.
В более общем случае, когда решетка освещается немонохроматическим (сложным, например, белым) светом, дифракционная картина усложняется (рис. 6.10).
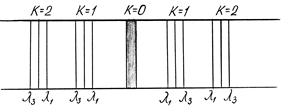
Рис. 6.10. Схематический вид дифракционного спектра
При k = 0 условие максимумов, удовлетворяется для всех длин волн, т.е. при j = 0 наблюдается центральная световая полоса, соответствующая неотклоненному пучку лучей такого цвета, каким был цвет источника.
При k = 1 симметрично по обе стороны от центральной полосы получаются дифракционные цветовые линии, от фиолетового до красного, соответствующие разным длинам волн, входящим в состав смешанного цвета. Эта группа линий называется спектрами 1-го порядка. Красная часть спектра отклонена больше, чем фиолетовая.
При k = 2 получают аналогичные спектры 2-го порядка. Линии спектров высоких порядков менее интенсивны, и на практике ясно наблюдаются спектры не выше 3-го порядка.
Рассмотрим один из методов определения длины волны при помощи дифракционной решетки. Освещая дифракционную решетку 2 (рис. 6.10) с помощью лазера 1 на расположенном за ней экране 3, можно получить четкую дифракционную картину без использования фокусирующей линзы.
Так как в установке используется монохроматическое лазерное излучение, то дифракционная картина будет представлять собой ряд ярких симметрично расположенных пятен (максимумов), интенсивность которых убывает при смещении влево и вправо от центра дифракционной картины.
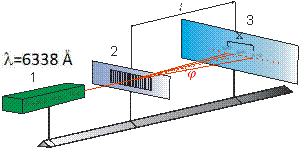
Рис. 6.10. Схема установки для определения постоянной дифракционной решетки: 1 – лазер; 2 – дифракционная решетка; 3- экран; l - расстояние от решетки до экрана; х - расстояние между центрами максимумов одноименных порядков
Для определения длины волны по формуле (6.8) необходимо знать sin j. Так как l >> х, то
sin j » tg j =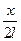 
.
Подставляя значения в выражение (6.8), получим окончательную формулу для нахождения длины волны
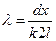. (6.10)
Длина волны измеряется в микрометрах (1 мк = 10–6 м), нанометрах (1 нм =10-9 м) или ангстремах (1 Å = 10–10 м).
В данном задании необходимо вычислить постоянную дифракционной решетки, выразив ее из формулы (6.10),
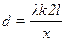(6.11)
и рассчитать число штрихов на 1 мм:
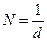, (6.12)
значение N выражается в мм–1. Для измерений используют две дифракционные решетки.