Порядок выполнения работы задания № 6.2

1. Включить Не-Ne лазер (l = 6328 Å) в сеть переменного тока. Установить экран на таком расстоянии от дифракционной решетки, чтобы на нем получилось четкое изображение центральной полосы и спектров 1-го и 2-го порядков.

2. Измерить расстояние от экрана до дифракционной решетки.

3. Измерить линейкой на экране расстояние между серединами красных полос спектров 1-го и 2-го порядков.

4. Значения d и N вычислить по формулам (6.11), (6.12).

5. Полученные экспериментальные данные и расчетные значения заносить в табл. 6.2. Оценить погрешности измерений.

6. Для второй дифракционной решетки заполняют аналогичную табл. 6.2.

Таблица 6.2

№ п/п	Расстояние между серединами спектров 1-го порядка х1, мм	Расстояние между серединами спектров 2-го порядка х1, мм	Расстояние от решетки до экрана l, мм
1-я дифракционная решетка
…
Среднее значение постоянной решетки
Число штрихов на 1 мм

Контрольные вопросы к заданию 6.2

1. Что представляет собой дифракционная решетка? Каковы параметры, характеризующие дифракционную решетку (постоянная, период, разрешающая способность, угловая и линейная дисперсия)?

2. Как выглядит дифракционная картина при дифракции на решетке? Дать качественное и количественное описание.

3. Какая связь существует между дифракцией и интерференцией?

Рекомендуемая литература: [1], [4], [11], [12], [14].

Лабораторная работа 7

ИССЛЕДОВАНИЕ ОПТИЧЕСКИХ СИСТЕМ

Задание 7.1. Определение фокусного расстояния

Собирающей линзы методом Бесселя

Приборы и принадлежности: экран, линза, осветитель, оптическая скамья и рейтеры, линейка

Цель задания: экспериментальное определение фокусного расстояния собирающей линзы методом Бесселя.

Краткая теория

Линзой называется прозрачное тело (обычно из стекла), ограниченное двумя сферическими поверхностями. Одна из поверхностей линзы может быть плоской (т.е. иметь бесконечно большой радиус кривизны). Линза - простейший частный случай центрированной оптической системы и обладает всеми ее свойствами.

В теории Гаусса описывается идеальная оптическая система, т.е. система, в которой сохраняется гомоцентричность пучков и изображение геометрически подобно предмету. Это есть чисто геометрическая теория, устанавливающая соотношения между точками, линиями и плоскостями в пространстве предметов и пространстве изображений.

Прямая, соединяющая центры сферических поверхностей точки О₁ и О₂ (рис. 7.1), представляет собой ось симметрии центрированной системы и называется ее главной оптической осью. Теория Гаусса устанавливает шесть так называемых кардинальных точек одномерных кардинальных плоскостей, задание которых полностью определяет все свойства оптической системы.

Учитывая, что кардинальные точки не являются линейно независимыми для описания центрированной системы (в том числе и для построения изображений), оказывается достаточным задание четырех из них.

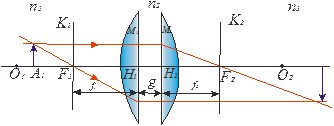
Рис. 7.1. Центрированная оптическая система: F₁ , F₂ – передний и задний фокусы; K₁F₁, K₂F₂ – передняя и задняя главные точки системы; M₁H₁, M₂H₂ – передняя и задняя главные плоскости

Точки F₁ и F₂ называются передним и задним фокусом системы, если сопряженные с ними точки находятся в бесконечности.

Следовательно, в фокусах F₁ и F₂ пересекаются лучи, падающие на оптическую систему (соответственно справа и слева) параллельно ее главной оптической оси. Фокусы F₁ и F₂ являются кардинальными точками системы, а проходящие через них перпендикулярно главной оптической плоскости – кардинальными фокальными плоскостями системы.

Две перпендикулярные главной оптической оси плоскости М₁Н₁ и М₂Н₂, точки которых сопряжены и изображаются с увеличением, равным +1 (т. е. плоскость М₁Н₂ изображается на М₂Н₂ прямо, в натуральную величину), называются главными плоскостями системы, а точки пересечения этих плоскостей с главной оптической осью – главными точками. Главные плоскости и главные точки - также кардинальные элементы системы.

Передним фокусным расстоянием системы называется расстояние F₁ = F₁H₁, т. е. расстояние от переднего фокуса до передней главной точки, аналогично задним фокусом называется расстояние F₂ = H₂F₂ .

Можно показать, что если показатели преломления пространства предметов n₁ и пространства изображений n₃ равны (n₁ = n₃) , то переднее и заднее фокусные расстояния системы также равны (F₁ = F₂).

На рис. 7.1 дан возможный вариант построения изображения A₂B₂ предмета A₁B₁ с учетом свойств, рассмотренных кардинальных элементов системы.

В зависимости от вида ограничивающих поверхностей линзы бывают двояковыпуклыми, плосковыпуклыми, двояковогнутыми, плосковогнутыми и вогнуто-выпуклыми. На рис. 7.2 изображены различные типы линз и их главные плоскости.

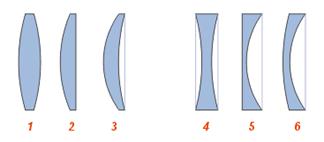
Рис. 7.2. Типичные линзы с указанием их главных плоскостей:

собирающие: 1 — двояковыпуклая, 2 — плоско выпуклая, 3 — вогнуто-выпуклая (положительный (выпуклый) мениск);

рассеивающие: 4 — двояковогнутая, 5 — плоско вогнутая, 6 — выпукло-вогнутая (отрицательный (вогнутый) мениск);

Как видно из рис. 7.2, главные плоскости (главные точки) могут лежать как внутри, так и вне линзы совершенно несимметрично относительно ее поверхностей.

Если толщина линзы достаточно мала по сравнению с радиусами кривизны ограничивающих ее поверхностей и можно считать, что передняя и задняя главные плоскости, передняя и задняя поверхности пересекают главную оптическую ось в одной общей точке, то линзу называют тонкой, а точку пересечения слившихся плоскостей с главной оптической осью – оптическим центром линзы. В этом случае переднее и заднее фокусные расстояния линзы отсчитываются от ее оптического центра.

Рассмотрим тонкую собирающую линзу (рис. 7.3). Будем предполагать, что n₁ = n₃ = 1; n₂ = n; F₁ = F₂ = F.

Конкретизируем сформулированные ранее свойства оптической системы применительно к этому частному случаю.

На рис. 7.3 оптический центр - это точка О, проходя через которую лучи не изменяют направления.

Всякая прямая, проходящая через оптический центр, называется оптической осью, и если она, кроме того, проходит через центры кривизны (O₁ и O₂) – главной оптической осью.

Плоскость, перпендикулярная главной оптической оси и проходящая через опти­ческий центр, называется главной плоскостью линзы.

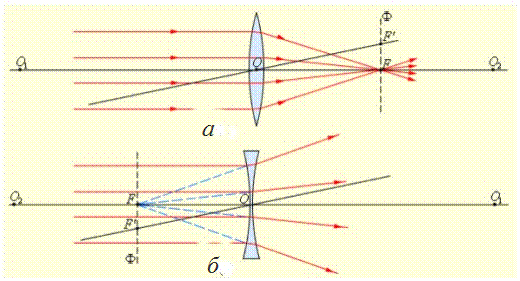
Рис. 7.3. Преломление параллельного пучка лучей: а – в собирающей; б – рассеивающей линзах. Точки O₁ и O₂ – центры сферических поверхностей; O₁O₂ – главная оптическая ось, O – оптический центр, F – главный фокус; F' – побочный фокус, OF' – побочная оптическая ось;Ф – фокальная плоскость

Главным фокусом линзы называется точка, в которой пересекаются после преломления в линзе лучи, падающие на нее пучком, параллельным главной оптической оси (на рис. 7.3 точки F). Расстояние главного фокуса от оптического центра линзы (расстояние ОF₁ и ОF₂) называется главным фокусным расстоянием и является основной характеристикой линзы. Для собираю­щих линз главное фокусное расстояние – величина положительная, для рассеивающих – отрицательная. Часто лин­зу характеризуют оптической силой D = 1/F – величиной, обратной главному фокусному расстоянию, выраженному в метрах (если линза находится в среде с показателем преломления, отличным от 1, оптическая сила линзы D = n / F, где n – показатель преломления среды). Для рассеивающих линз главный фокус мнимый, для его отыскания берут не сами лучи, а их продолжение (рис. 7.1).

Для построения изображения предмета с помощью линзы пользуются лучами, ход которых через линзу известен. Обычно берут два луча из следующих трёх: 1 - проходит через оптический центр (идёт через линзу не преломляясь); 2 – падает на линзу параллельно её главной оптической оси (при выходе из линзы пройдет через её главный фокус); 3 - проходит через главный фокус линзы (он из линзы выйдет параллельно её главной оптической оси) (рис. 7.4).

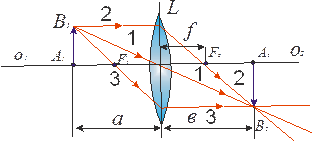
Рис. 7.4. Лучи, используемые для построения изображений в линзах

Изображение предмета AB в­ зависимости от того, на каком расстоянии от линзы он будет находиться, может получиться увеличенным или умень­шенным, действитель­ным (как на рисунке) или мнимым.

Делая построение изображения, мы ограничились лучами, образующими малые углы с оптической осью линзы (параксиальные лучи). Обозначим через a (рис. 7.4) расстояние от предмета до линзы, а через в – расстояние от лин­зы до изображения. Зависимость между a, в и F (фокусным расстоянием) даёт нам формулу тонкой линзы

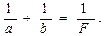(7.1)

Линейное увеличение, даваемое тонкой линзой, равно

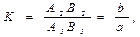(7.2)

т. е. линейным увеличением называется отношение размера изображения предмета к соответствующему размеру предмета.

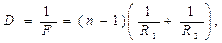Оптическая сила тонкой линзы может быть рассчитана по формуле

(7.3)

где F – фокусное расстояние линзы; R₁ и R₂ – радиусы кривизны первой и второй преломляющих поверхностей линзы, считаемые по ходу луча света; n – показатель преломления материала линзы. Радиусы выпуклых поверхностей считаются положительными, вогнутых – отрицательными.

При определении фокусного расстояния собирающей линзы обычно применяют формулу тонкой линзы. Однако положение оптического центра линзы не всегда известно, поэтому расстояние f находят не непосредственно, а используя метод перемещения линзы – метод Бесселя.

Определение фокусного расстояния собирающей линзы по методу ее перемещения сводится к следующему.

Если расстояние от предмета до изображения больше 4f, то всегда найдутся два таких положения линзы, при которых на экране получается отчетливое изображение предмета: в одном случае увеличенное, в другом – уменьшенное (рис. 7.5).

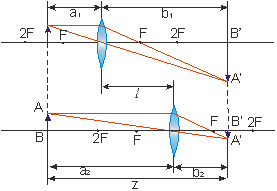
Рис. 7.5. Схема измерения фокусного расстояния линзы

по методу Бесселя

Для одного положения линзы расстояние от предмета до линзы и от линзы до изображения обозначим через a₁ и b₁, а для другого – a₂ и b₂. Так как расстояние между экраном и предметом остаётся неизменным, то

a₁+b₁=a₂+b₂.

Из этого равенства и равенства 1/F= (a+b)/(ab), которое представляет собой преобразованную формулу тонкой линзы, заключаем, что совместное существование указанных формул возможно только в том случае, когда a₁=b₂ и a₂=b₁. Обозначив расстояние между обоими положениями линзы через l, получим

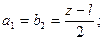
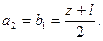
Подставляя эти значения в формулу линзы и решая относительно главного фокусного расстояния, получим

;

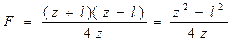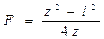(7.4)

Формула (7.4) носит название формулы Бесселя.

Если рассматривать реальную толстую линзу, то главные ее плоскости не будут совпадать, образуя оптический центр линзы. Метод Бесселя применим и в этом случае. Формула для вычисления фокусного расстояния, помимо введенных ранее величин z и l, будет содержать величину g – расстояние между главными плоскостями линзы (см. рис. 7.1)

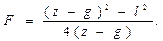(7.5)

Для расчета фокусного расстояния F по формуле (7.5) необходимо знать величину g. Для ее определения можно повторить опыт, взяв другое расстояние z₁ между предметом (спиралью лампы) и экраном:

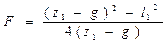. (7.6)

Решая совместно уравнения (7.5) и (7.6), можно определить F и g.

Для упрощения расчета в последних формулах можно пренебречь g² по сравнению с z², тогда для расчета фокусного расстояния линзы получим выражение

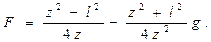(7.7)