Тема: «Решение прямой и обратной геодезических задач»

Цель: Освоить навыки в вычислении координат точек, дирекционных углов и длин линий.

Оборудование: Рабочая тетрадь, учебник, конспект, методические рекомендации.

Задание:

1. По исходным данным решить задачи

2. Составить схематические чертежи по решению задач.

3. Сделать вывод о выполненной работе.

Порядок выполнения работы:

8. Ознакомиться с краткими теоретическими сведениями.

9. Решить задачи по своему варианту в соответствии с заданием.

10. Ответить на контрольные вопросы.

11. Сдать отчёт.

Краткие теоретические сведения

При проведении геодезических работ на строительной площадке возникает необходимость в определении положения линий на местности относительно какого-либо направления, принятого за начальное.

Ориентировать линию – значит определить её направление относительно исходного.

Истинным или географическим меридианом называется линия пересечения земной поверхности плоскостью, проходящей через данную точку и ось вращения Земли.

Магнитным меридианом называется направление оси магнитной стрелки компаса, расположенного в данной точке.

Осевым меридианом называется средний истинный меридиан зоны.Угол δ, отсчитываемый от северного направления истинного меридиана Ν_и до магнитного меридиана Ν_м, называется склонением магнитной стрелки.

Угол γ, отсчитываемый от северного направления истинного меридиана Ν_и до параллели осевому меридиану Ν_о, называется сближением меридианов.

Азимутом А называется угол, отсчитываемый по ходу часовой стрелки от северного направления меридиана до данной линии. Изменяется в пределах от 0^ᵒ до 360^◦.

Дирекционным углом α называется угол, отсчитываемый по ходу часовой стрелки от северного направления осевого меридиана зоны до данной линии.

Ν_и Ν_м

Ν_о

А_m А_и

О α

В

Рис.10

А_и = α + γ;

А_и = А_м + δ; отсюда

α + γ = А_м + δ;

α = А_м + δ – γ

Сущность прямой геодезической задачи состоит в том, что по координатам исходной точки А и полярному углу α направления АВ, требуется определить координаты другой точки В. Так как в практике прямоугольные координаты не измеряют, то для решения задачи измеряют полярный угол α и расстояние d (рис.10).

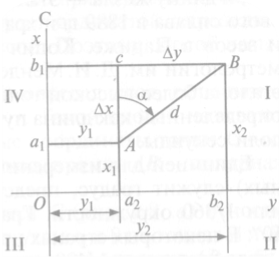Рис.11

Дано: Решение:

Х_А Х_В = Х_А 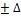Х

У_А У_В = У_А У

α Х = d , У = d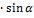

d

Определить:

Х_В, У_В

Для выноса проекта на местность бывает необходимо по данным прямоугольных координат найти значение дирекционного угла и длину линии между заданными точками. Это и составляет сущность решения обратной геодезической задачи.

Дано: Решение:

Х_А, У_А tg α_А-В = = ;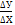

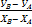Х_В, У_В по знакам числителя и знаменателя

Определить: определяем название румба линии АВ, а следовательно

α_А-В, d_А-В и дирекционный угол.

d_А-В = = = = ;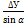

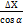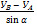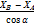d_А-В = = ;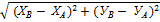

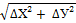Пример 1

Дано: Решение:

Х₁ = 255,35 м Х₂ = Х₁ 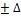Х ; У₂ = У₁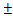 У; α = 155^ᵒ 30^′ ;

У₁ = 538,80 м ЮВ: r =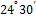

α = 155^ᵒ 30^′ Х = d 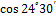= 98,37 0,90996 = 89,51 м (–)

d = 98,37 м У = d 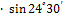= 98,37 0,41469 = 40,79 м (+)

Х₂ = 255,35 – 89,51 = 165,84 м

Определить: У₂ = 538,80 + 40,79 = 579,59 м

Х₂, У₂

Схема решения прямой геодезической задачи.

Х

( + )

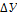1 У

( – )

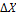
Рис. 12

Пример 2

Дано: Решение:

Х₁ = 287,35 м tg α = 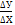; Х = Х₂ – Х₁ = 155,85 – 287,35 = – 131,50 м

У₁ = 572,82 м У = У₂ – У₁ = 482,32 – 572,82 = – 90,50 м

Х₂ = 155,85 м tg α = 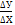= = 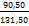0,6882 ; т.к. Х и У имеют знак (–),

У₂ = 482, 32 м румб линии будет ЮЗ tg r = 0,6882; r = 34^ᵒ 32^′ ,

Определить: соответственно α = 180^ᵒ + 34^ᵒ 32^′ = 214^ᵒ 32^′

α_1-2 ; d_1-2 ; d = = = = ;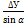

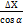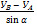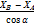d = 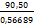= 159,64 м ; d = 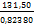= 159,63 м

d = 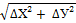= = 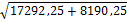159,63 м

за окончательное значение принимаем 159,63 м.

Схема решения обратной геодезической задачи.

Х

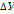( – ) 1

У

( – )

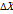Рис. 13

Варианты заданий Табл. 2

№ вар.	Прямая задача	Обратная задача
Х1 м	У1 м	α 1-2	d1-2 м	Х1 м	У1 м	Х2 м	У2 м
	250,00	370,00	78ᵒ35′	95,90	155,80	280,30	320,40	200,80
	150,00	270,00	92ᵒ40′	105,20	355,30	240,70	270,90	290,20
	175,30	320,20	64ᵒ25′	88,40	215,75	310,90	295,25	240,40
	213,45	375,85	105ᵒ45′	115,65	265,15	415,70	290,65	450,20
	225,75	325,15	182ᵒ35′	150,30	375,25	370,55	250,75	420,15
	236,85	370,45	153ᵒ30′	121,12	253,28	325,75	290,50	387,25
	241,90	400,25	200ᵒ45′	136,28	276,60	338,15	231,85	390,70
	255,15	411,30	125ᵒ15′	142,31	292,41	340,36	243,16	315,86
	269,23	425,78	220ᵒ35′	158,34	315,37	342,57	365,87	265,27
	283,31	439,26	300ᵒ45′	164,47	338,63	344,78	298,28	365,28
	297,39	453,52	275ᵒ24′	180,60	320,40	270,90	240,70	355,30
	311,45	355,30	335ᵒ28′	98,43	265,15	155,80	320,40	215,75
	325,59	390,80	55ᵒ50′	101,75	280,30	240,70	155,80	320,40
	121,15	251,65	101ᵒ18′	112,65	215,75	280,30	320,40	155,80
	132,26	248,36	195ᵒ24′	123,76	265,15	240,70	155,80	265,15
	143,37	259,47	302ᵒ36′	134,87	450,20	390,70	415,70	265,15
	154,48	270,58	15ᵒ30′	155,80	320,40	215,75	280,30	265,15
	265,15	355,30	96ᵒ24′	215,75	415,70	265,15	155,80	450,20
	280,30	320,40	190ᵒ36′	280,30	355,30	270,90	365,28	298,28
	355,30	155,80	275ᵒ40′	265,15	251,65	132,26	143,37	248,36
	240,70	270,90	115ᵒ20′	280,30	259,47	225,75	325,15	213,45
	276,60	338,15	303ᵒ50′	320,40	132,26	251,65	121,15	390,80
	390,70	231,85	55ᵒ52′	415,70	297,39	453,52	251,65	355,30
	290,65	415,70	201ᵒ21′	215,75	325,59	311,45	355,30	453,52
	265,15	231,85	78ᵒ45′	280,30	297,39	325,59	121,15	311,45
	450,20	290,65	130ᵒ26′	320,40	453,52	390,80	311,45	325,59
	270,90	338,15	221ᵒ18′	338,63	439,26	269,23	425,78	283,31
	390,70	265,15	288ᵒ12′	292,41	355,30	425,78	453,52	269,23
	415,70	270,90	350ᵒ00′	276,60	411,30	255,15	400,25	241,90
	290,65	450,20	260ᵒ50′	253,28	298,28	439,26	311,45	425,78
	276,60	390,70	175ᵒ28′	375,25	269,23	425,78	355,30	297,39
	231,85	338,15	80ᵒ08′	265,15	241,90	411,30	269,23	425,78
	155,80	215,75	125ᵒ11′	215,75	121,15	325,59	251,65	390,80
	265,15	280,30	193ᵒ22′	355,30	213,45	259,47	225,75	248,36
	355,30	320,40	282ᵒ33′	155,80	251,65	132,26	213,45	143,37
	240,70	276,60	315ᵒ30′	292,41	325,15	251,65	390,80	297,39
	320,40	338,15	225ᵒ44′	320,40	439,26	297,39	311,45	325,59
	265,15	415,70	135ᵒ55′	265,15	390,80	439,26	453,52	259,47
	270,90	338,15	45ᵒ18′	215,75	225,75	248,36	132,26	325,15
	265,15	390,70	345ᵒ28′	155,80	251,65	453,52	297,39	390,80

Контрольные вопросы

1. Дайте определение дирекционного угла.

2. Дайте определение румба.

3. Зависимость между дирекционными углами и румбами.

4. Что такое приращения координат?

5. Назовите четверти и знаки в приращениях координат.

Содержание отчёта

1. Номер практической работы

2. Тема

3. Результат работы

4. Оборудование

5. Задание

6. Ответы на контрольные вопросы

7. Выполнение практических индивидуальных задач

8. Вывод о выполненной работе.