Пересечение поверхности с плоскостью. Алгоритм. Пример
Построение сечений
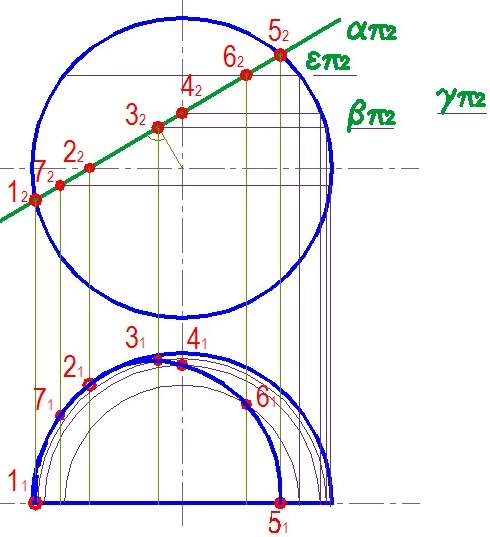 1)Анализ заданной поверхности. Если секущая плоскость частного положения, то одна проекция сечения на чертеже совпадает с линией следа плоскости.
1)Анализ заданной поверхности. Если секущая плоскость частного положения, то одна проекция сечения на чертеже совпадает с линией следа плоскости.
2)Определение характерных точек, принадлежащих линии пересечения. Задача сводится к определению проекций отмеченных точек на другой плоскости проекций.
3)Проведение вспомогательной секущей плоскости – посредника - частного положения – горизонтальной или фронтальной. Выбор основан на получении в сечении простых геометрических фигур – треугольников, окружностей, прямоугольников.
4)Построение линий пересечения вспомогательной плоскости с заданными поверхностью и плоскостью.
5)Определение точек пересечения построенных линий.
6)Повторение пунктов 3, 4, 5 n раз.
7)Соединение полученных точек с учетом видимости.
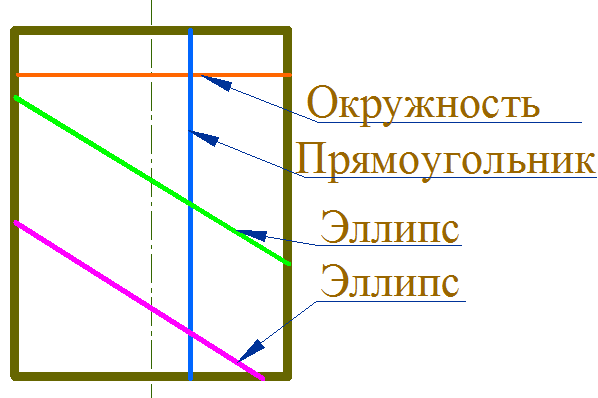
Виды линий пересечения у поверхностей цилиндра.
Случаи пересечения поверхностей. Общий случай. Алгоритм. Пример.
Способ посредников. Проведение вспомогательной секущей плоскости или поверхности, которые выбираются из условия получения в сечении простых линий.
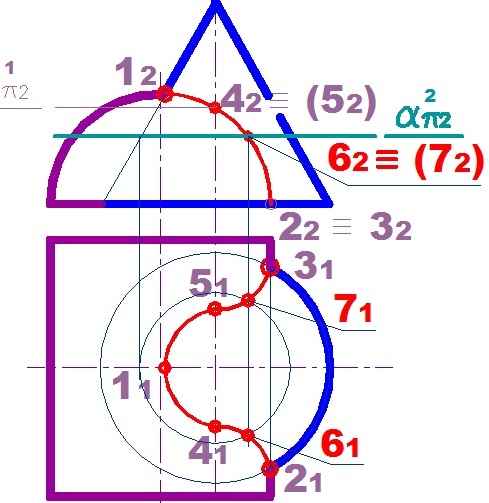
Частный случай пересечения поверхностей. Пример.
Анализ поверхности: определить наличие проецирующей поверхности. В этом случае на одной из плоскостей проекций уже имеется одна проекция линии пересечения.
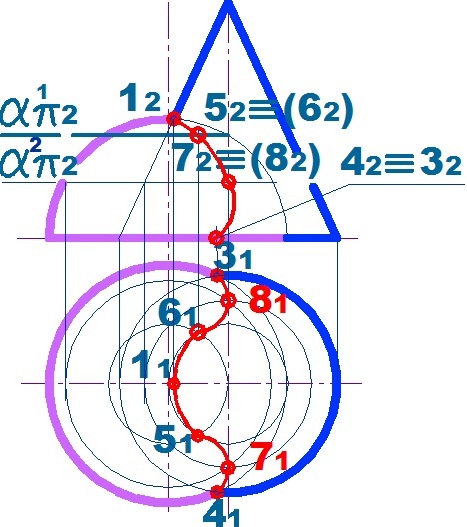
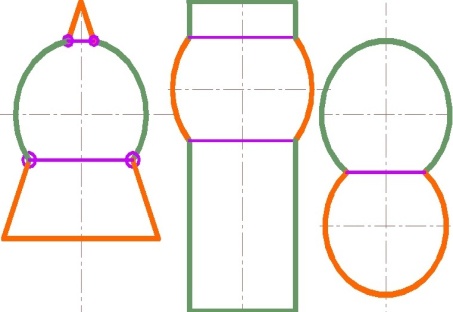
Особый случай пересечения поверхностей по теореме Монжа. Пример.
Линия пересечения определяется пространственно и по теореме Монжа.
Теорема Монжа: две поверхности вращения, описанные вокруг третьей, пересекаются между собой по двум кривым второго порядка, которые проецируются на плоскость, параллельную осям вращения в виде прямолинейных отрезков, соединяющих точки пересечения очерковых образующих.
Определение развертки поверхности, применение. Развертываемые и не развертываемые поверхности. Пример.
Разверткой , называется фигура , полученная при совмещении поверхности с плоскостью.Развертки широко применяютсяв практике и технике при изготовлении изделий из листового материала. Корпуса автобусов, самолетов, судов. В теплоэнергетике и теплотехнике - воздуховоды, вентиляционные каналы и т. д.
Развертываемые поверхности- многогранные поверхности и торсы (поверхности с ребром возврата, цилиндрические и конические поверхности).
Не развертываемыеповерхности не могут быть совмещены с плоскостью (хотя в практике для них приходится строить условные развертки).(тор, сфера)
