Решение четырех основных задач преобразованием комплексного чертежа способом вращения вокруг проецирующей оси
Задача №1
Перевести прямую общего положения - в частное, т.е. чтобы прямая общего положения после поворота оказалась параллельной одной из плоскостей проекций. Прямую АВ (рис. 4-46) поставить в положение фронтали.
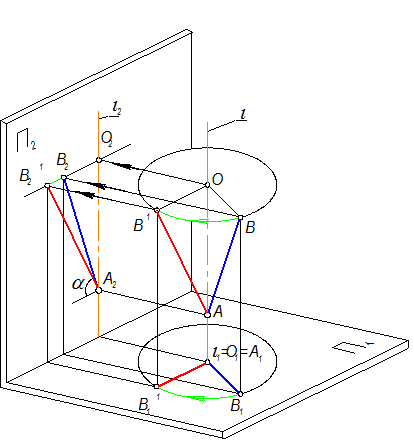
Рис. 4-46
Чтобы прямую АВ (рис 4-47 а) поставить в положение фронтали, необходимо установить А1В1 ^ линиям связи (А1В1 ^ А1А 2)
Алгоритм(рис. 4-47)
1. Выбираем ось вращения i ^ П1; i É А (рис. 4-47б)
2. Радиус вращения: R = | А В |.
3. Вращаем А1В1 вокруг оси i1 = А1 до положения, когда А1В1 станет ^ А1А2. (рис. 4-47в)
4. Точка А2 останется на оси i2, все другие точки прямой переместятся по прямым, перпендикулярным линиям связи. Точка В2 переместится в положение В2’.
5. Отрезок АВ’ - фронталь Þ | АВ | = |А2В2’| (рис. 4-47г)
6. Угол a - угол наклона АВ к П1.
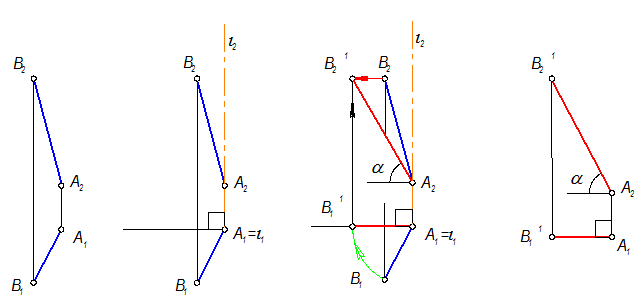
| а) AB – прямая общего положения | б) i ^ П1 | в) Прямая AB заняла положение фронтали | г) AB(AB’) - фронталь |
Рис. 4-47
Задача №2
Прямую общего положения СD поставить в положение проецирующей прямой.
Алгоритм
1. Одним простым вращением нельзя прямую общего положения поставить в положение проецирующей, поэтому сначала решают задачу №1: прямую СD поставить в положение горизонтали.
2. Выбираем ось вращения i ^ П2; i É С (рис. 4-48, б)
3. Радиус вращения: R = | С2D2 |
4. Вращаем C2D2 вокруг оси i2 = C2 до положения, когда C2D2 станет ^ C1C2 (рис. 4-48 в).
5. Точка C1 останется на оси i1, все другие точки прямой переместятся по прямым, перпендикулярным линиям связи. Точка D1 переместится в положение D1’
6. Отрезок CD’ - горизонталь Þ | CD | = | C1D1’ | (рис. 4-48, г)
7. Угол b - угол наклона CD к П2.
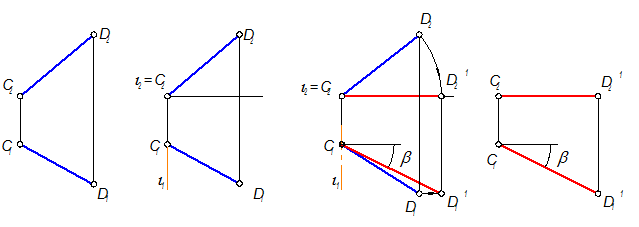
| а) CD – прямая общего положения | б) | в) Прямая CD заняла положение горизонтали | г) CD(CD’) - горизонталь |
Рис. 4-48
8. Проводим второе вращение. Ось i2 выбираем ^ П1, i 2 É D1; i12 = D11; i22 || D11D21 (рис. 4-49а);
9. Радиус вращения: R = | C1D11 |.
10. Вращаем C1D11 до положения, когда C1D11 станет || линиям связи, и станет равной С12D11 (точка D11 не вращается).
11. Точка С2, двигаясь по прямой, займет положение D21, т.е. С22 = D21 (рис. 4-49 в)
12. Отрезок С2D1 - проецирующий, С2D1 ^^ П2 .
13. Общий вид решения показан на рис. 4-49 б.
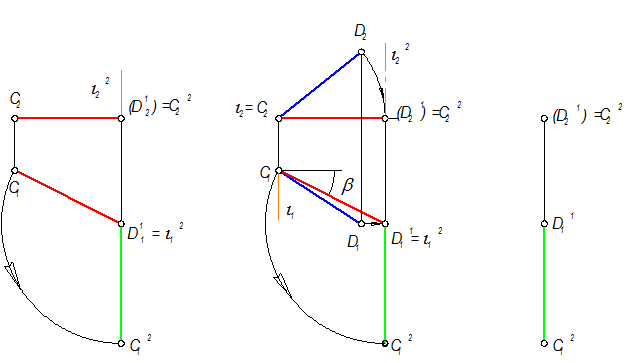
| а) Задача №2 | б) Задача №1 и №2 | в) CD(C2D1) – проецирующая прямая |
Рис. 4-49
Задача №3
Плоскость общего положения поставить в положение проецирующей, Г(АВС)^^ П2
Алгоритм
Рассмотрим преобразование плоскости общего положения Г(АВС) во фронтально проецирующую (Г ^ П2), но две плоскости ^ друг другу, если одна из них Г(АВС) содержит перпендикуляр к другой (П2). Что это за прямая? Такой прямой для Г(АВС) может быть только горизонталь, занимающая фронтально проецирующее положение (задача № 27 в рабочей тетради). Значит в плоскости Г(АВС) нужно провести горизонталь и повернуть ее горизонтальную проекцию || линиям связи.
1. Проводим в плоскости горизонталь h (h1 h2) через точку С.
2. Выбираем положение ось i1 ^ П1, i1 É С (рис. 4-50 а).
3. Поворачиваем горизонталь h вокруг оси пока она не займет положение h ^ П2, т.е. h1 || линиям связи, Rh = | C111 | (рис. 4-50 б)
4. Поворачиваем точки А и В в ту же самую сторону, на тот же самый угол, что и горизонталь, Rh = | С1А1 |, RB = | С1В1 | (рис. 4-50 в).
5. Фронтальные проекции точек А(А2) и В(В2) перемещаются по прямым, линиям связи и занимают положение А21 и В21.
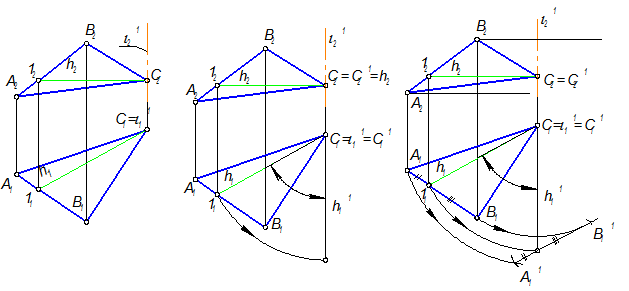
| а) Г(АВС) – плоскость общего положения | б) | в) |
Рис. 4-50
6. Плоскость Г займет фронтально проецирующее положение (Г21 -вырождается в прямую линию) Þ Г21 - главная проекция (рис.4-50 г).
7. Новое положение плоскости Г(Г21) показано на (рис. 4-50 д).
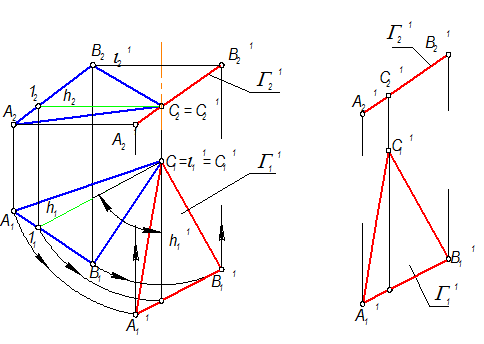
| г) Задача №3 | д) Плоскость Г(А1В1С1) ^^ П2 |
Рис. 4-50
Задача №4
Плоскость общего положения поставить в положение плоскости уровня, Г(АВС) || П1
Алгоритм
1. Одним простым вращением нельзя плоскость общего положения поставить в положение плоскости уровня, поэтому сначала решаем задачу №3 (рис. 4-50).
2. Произведем второе вращение. Ось вращения i2 ^^ П2, i2 É В1 (рис. 4-51 а).
3. Поворачиваем Г21 до положения, когда Г22 станет ^ линиям связи (рис. 4-51 б).
4. Точки А11, С11 переместятся по прямым до положения А12, С12.
5. Плоскость Г2 -плоскость уровня Þ Г22 - ее главная проекция, Г12 - натуральная величина DАВС.
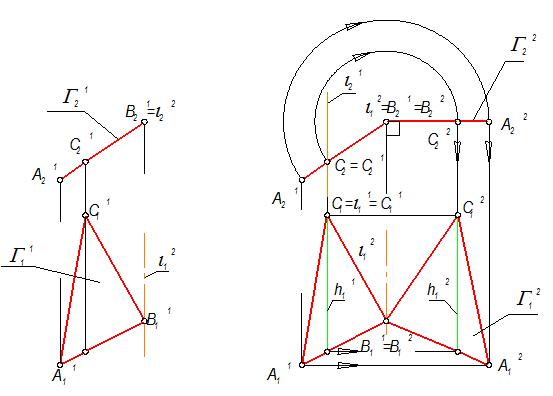
| а) Плоскость Г (А1В1С1) ^^ П2 | б) Задача №4 |
Рис. 4-51
6. Полное решение показано на рис. 4-51 в.
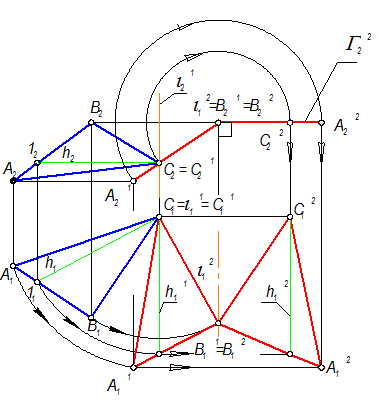
Задачи №3 и №4
Рис. 4-51в
