Учитывая это, из (4.5) получим
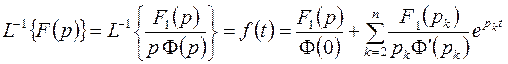(4.7)
Для удобства принимаем, что многочлен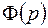 
имеет степень 
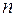(а не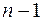 
), но тогда корни его 
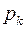будут нумероваться от 1 до 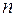. И потому формула (4.7) перепишется в виде
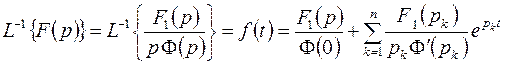(4.8)
Примечание. Простые корни 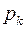знаменателя 
дроби 
являются ее простыми полисами. Используя формулу для вычисления вычетов функции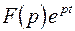 
относительно простых полюсов, формуле разложения (4.5) можно придать вид
,
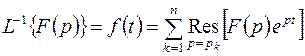Что совпадает с общим результатом (4.2).
Отметим, что формулы разложения (4.5),(4.8) иногда оказываются применимыми и в том случае, когда изображение имеет бесконечное число полюсов.
II. Знаменатель дроби (4.3) имеет кратные корни. Пусть числа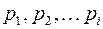 
являются корнями кратности 
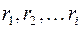соответственно, причем 
.
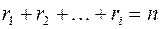Тогда
.
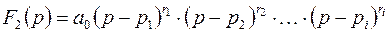Ввиду громоздкости процедуры определения коэффициентов разложения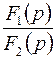 
на простейшие дроби в данном случае для отыскания оригинала 
будем исходить из формулы (4.2).
Кратные корни 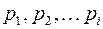знаменателя являются полюсами порядка 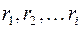дроби . Воспользовавшись формулой для вычета функции 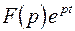относительно полюса порядка 
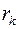, из формулы (4.2) получим
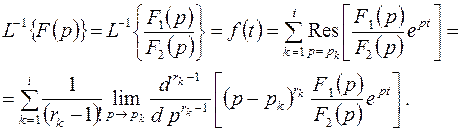(4.9)
В частности, когда все полюса простые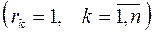 
, формула (4.9) принимает вид (4.8).
Итак, если изображение является дробно-рациональной функцией от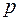 
и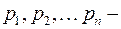 
ее полюса (простые или кратные), то соответствующий оригинал определяется формулой (4.9).
При практическом использовании формулы (4.9) полезно учитывать, что знаменатель содержит множитель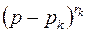 
и потому может быть записан в ви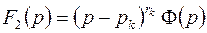де
, где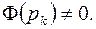 
Тогда
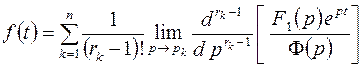(4.10)
Пример 4.4. По теореме разложения найти оригинал функции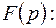 
а)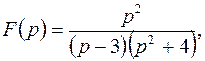 
б)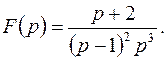 
Решение. а) по условию,
,
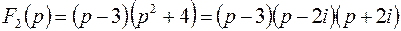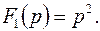Знаменатель имеет простые корни; 
, 
, 
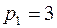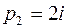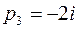. В соответствии с этим случаем воспользуемся формулой (4.5).
Тогда
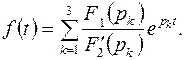
Здесь
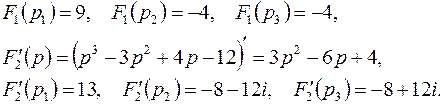
Следовательно,
.
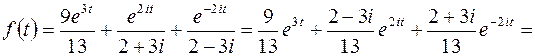
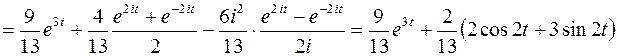б) здесь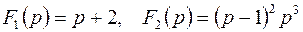 
. Функция имеет два полюса: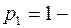 
полюс 2-го порядка, 
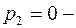полюс 3-го порядка. По формуле (4.9) находим
.
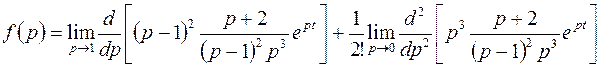Чтобы вычислить первое слагаемое, необходимо сначала найти производную, а затем перейти к пределу при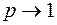 
.
.
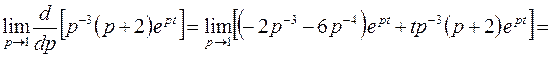
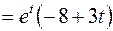Для второго слагаемого найдем производную первого порядка от выражения, стоящего в скобках:
.
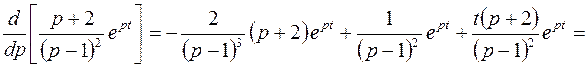
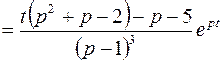Тогда
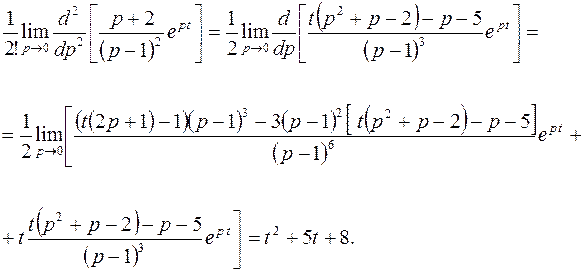
Итак,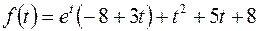 
.
5. ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Операционное исчисление можно рассматривать как своеобразный и эффективный метод интегрирования линейных дифференциальных уравнений и их систем, а также некоторых типов линейных дифференциальных уравнений в частных производных.
5.1. Решение линейных дифференциальных уравнений
с постоянными коэффициентами
Пусть дано линейное дифференциальное уравнение 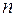-го порядка с постоянными коэффициентами
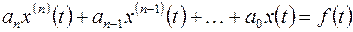, (5.1)
где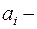 
действительные числа. Требуется найти решение 
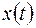этого уравнения для 
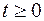, удовлетворяющее начальным условиям
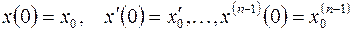. (5.2)