Плоскостью общего положения называют плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций
В общем случае ее изображение занимает все поле чертежа. Чтобы сделать чертеж более удобным и наглядным, плоскость общего положения ограничивают, задавая ее одним из следующих способов:
1. Тремя точками, не лежащими на одной прямой – Б(А, В, С);
2. Двумя параллельными прямыми – Д(а // b);
3. Двумя пересекающимися прямыми –Ж(cÇf/;
4. Точкой и прямой – 3 (М, м);
5. Отсеком плоскости - И (D АВС).
При этом всегда можно перейти от одного способа задания плоскости к другому.
Если плоскость по мере удаления от наблюдателя поднимается вверх, то такую плоскость называют восходящей.
И наоборот, если плоскость по мере удаления от наблюдателя понижается, то такую плоскость называют нисходящей.
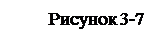
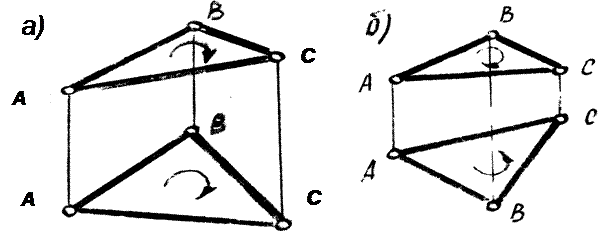На комплексном чертеже оба вида треугольника, которым задана восходящая плоскость, имеют одинаковые обходы (рис. 3-7а). Изображения треугольника, задающего нисходящую плоскость, имеют противоположные обходы (рисунок 3-7б).
Поскольку способов задания плоскости несколько и разных, будем считать, что на комплексном чертеже проекции восходящей плоскости ориентированы одинаково, а нисходящей - противоположно.
ВЗАИМОПРИНАДлЕЖНОСТЬ ТОЧКИ, ПРЯМОЙ И ПЛОСКОСТИ
Взаимное положение точки и прямой
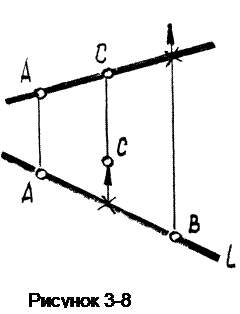Относительно прямой общего положения l(рисунок 3-8) построим следующие точки:
1. точка А принадлежитl (АÎl). Задача решается на основании свойства принадлежности;
2. точка В над прямой.
Как построить точку на прямой мы теперь знаем, а поскольку она должна быть над прямой, т, е. выше нее, необходимо внести соответствующее изменение в положение точки на виде спереди;
3. точка С за прямой.
Аналогично предыдущей задаче приходим к выводу, что запрямой означает дальше нее, чему соответствует изменение положения точки на виде сверху.
Точка и плоскость, прямая и плоскость
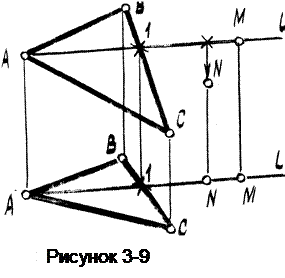Дана плоскость общего положения Б ( DАВС), (рисунок 3-9).
Построим точку М на плоскости Б и точку N под плоскостью Б.
Чтобы построить точку на плоскости, необходимо:
1) на этой плоскости Б провести (или выделить) любую прямую l, для чего провести прямую l через две точки принадлежащие плоскости (в нашем случае т.т. А и 1);
2) на этой прямой взять произвольную точку, например М (свойство принадлежности).
Чтобы построить точку N под заданной плоскостью, необходимо вначале, как сказано выше, найти точку, принадлежащую плоскости, а затем, на, виде спереди изображение ее опустить ниже прямой l (значит и ниже плоскости).
ЛЕКЦИЯ №4
Деление отрезка в заданном отношении
ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА И УГЛОВ ЕГО НАКЛОНА К ПЛОСКОСТЯМ УРОВНЯ.
УСЛОВИЯ ВИДИМОСТИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ.