Ортогональное проецирование. Свойства ортогонального проецирования
Ортогональное (прямоугольное) проецирование является частным случаем параллельного проецирования, когда направление проецирования перпендикулярно к плоскости проекций (s^П1). В этом случае проекции геометрических фигур называются ортогональными.
Ортогональному проецированию присущи все свойства параллельного проецирования, а также свойства, присущие только ортогональному проецированию.
Первое свойство. В общем случае ортогональная проекция отрезка всегда меньше его натуральной длины.
Если провести А*В || А1В1, то ÐАА*В = 90°. Из прямоугольного треугольника следует, что АВ - гипотенуза, А*В - катет, а гипотенуза всегда больше катета (А*В = АВ ´ Соsa),
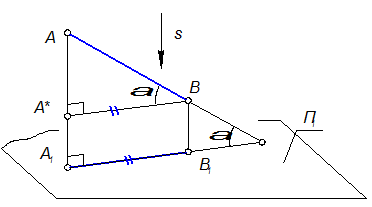
Рис. 1-11
Рассмотрим частные случаи:
Если a = 0 Þ |А1В1| = |АВ|, т.е. проекция равна самому отрезку.
Если a =90° Þ А1 = В1, т.е. проекция отрезка - точка.
Второе свойство: теорема о проецировании прямого угла
Если одна сторона прямого угла параллельна какой-нибудь плоскости проекций, а вторая сторона не перпендикулярна ей, то на эту плоскость проекций прямой угол проецируется без искажения.
Дано: ÐАВС = 90°, ВС || П1,
Доказательство:
плоскость Ф = АВ Ç ВВ1
плоскость S = ВС Ç ВВ1
ВС ^ Ф, т.к. ВС ^ АВ и ВС ^ ВВ1, но В1С1 || ВС Þ В1С1 ^ Ф Þ В1С1 ^ А1В1,
значит ÐА1В1С1 - прямой
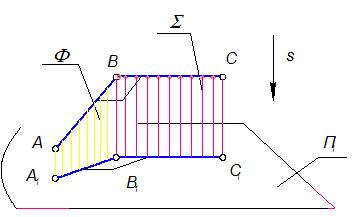
Рис. 1-12
Третье свойство: ортогональная проекция окружности в общем случае есть эллипс.
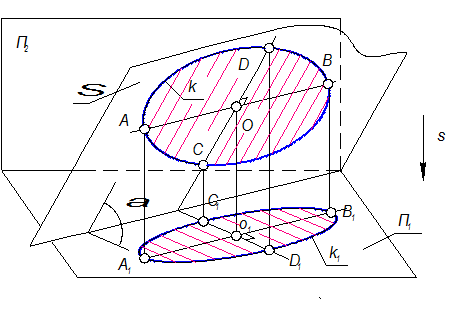
Рис. 1-13
Заключим окружность в плоскость S, S Ù П1 = a, если 0 < a < 90°, то окружность (k) -эллипс (k1)
АВ ^ СD - сопряженные диаметры, пусть АВ || П1
А1В1 = АВ - большая ось эллипса
С1D1 = СD ´ cоsa - малая ось эллипса.
Все хорды окружности параллельные СD проецируются с коэффициентом сжатия cоsa и делятся осью А1В1 пополам, т.е. ортогональная проекция окружности, в общем случае, есть замкнутая центрально симметричная кривая второго порядка, имеющая две взаимно перпендикулярные оси.
Частные случаи:
1. Если S || П1, то окружность (k) - проецируется без искажения.
2. Если S ^ П1, т.е. Ða = 90°, то окружность (k) - прямая линия, равная диаметру.
Метод Монжа
В машиностроительных чертежах используется метод прямоугольных проекций. Поэтому дальнейшее изучение курса будем вести, используя метод ортогонального проецирования.
Чтобы однозначно решить две основные задачи курса начертательной геометрии, чертежи должны удовлетворять следующим требованиям:
1. Простота и наглядность;
2. Обратимость чертежа.
Рассмотренные методы проецирования с использованием однокартинных чертежей позволяют решать прямую задачу (т.е. по данному оригиналу построить его проекцию). Однако, обратную задачу (т.е. по проекции воспроизвести оригинал) решить однозначно невозможно. Эта задача допускает бесчисленное множество решений, т.к. каждую точку А1 плоскости проекций П1 можно считать проекцией любой точки проецирующего луча lА, проходящего через А1. Таким образом, рассмотренные однокартинные чертежи не обладают свойством обратимости.
Для получения обратимых однокартинных чертежей их дополняют необходимыми данными. Существуют различные способы такого дополнения. Например, чертежи с числовыми отметками.
Способ заключается в том, что наряду с проекцией точки А1 задаётся высота точки, т.е. её расстояние от плоскости проекций. Задают, также, масштаб. Такой способ используется в строительстве, архитектуре, геодезии и т. д. Однако, он не является универсальным для создания чертежей сложных пространственных форм.
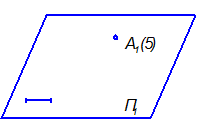
Рис. 1-14
В 1798 году французский геометр-инженер Гаспар Монж обобщил накопленные к этому времени теоретические знания и опыт и впервые дал научное обоснование общего метода построения изображений, предложив рассматривать плоский чертёж, состоящий из двух проекций, как результат совмещения двух взаимно перпендикулярных плоскостей проекций. Отсюда ведёт начало принцип построения чертежей, которым мы пользуемся и поныне.
Поставим перед собой задачу построить проекции отрезка [AB] на две взаимно перпендикулярные плоскости проекций П1 и П2.
