Движение потока на криволинейном участке русла

Задача №1.

Определить расход 75%-ной обеспеченности для многолетнего ряда наблюдений на реке Пижма в створе г. Советска. Построить гидрограф стока для расхода 75%-ной обеспеченности и определить объем годового стока.

Пи́жма (луговомар. Пижма) — река в Нижегородской и Кировской областях России, правый приток Вятки (бассейн Волги).

Длина 305 км, площадь бассейна 14 660 км². Средний расход воды 90 м³/сек. Замерзает в середине ноября, вскрывается во 2-й половине апреля. Питание главным образом снеговое.

№	год	Q0	№	год	Q0
		65,32			64,98
		34,28			98,77
		54,66			78,93
		89,21			89,32
		111,28			115,32
		265,34			132,54
		78,32			25,66
		45,69			45,68
		94,25			79,85
		47,47			45,69
		29,32			87,98
		65,32			99,32
		45,88			89,95
		210,22			99,34
		49,85			150,3
		45,68	Q0 (норма стока)	85,49844

Решение: по результатам многолетних наблюдений строим номограмму (рис.1) и откладываем норму стока Q₀ на ней.

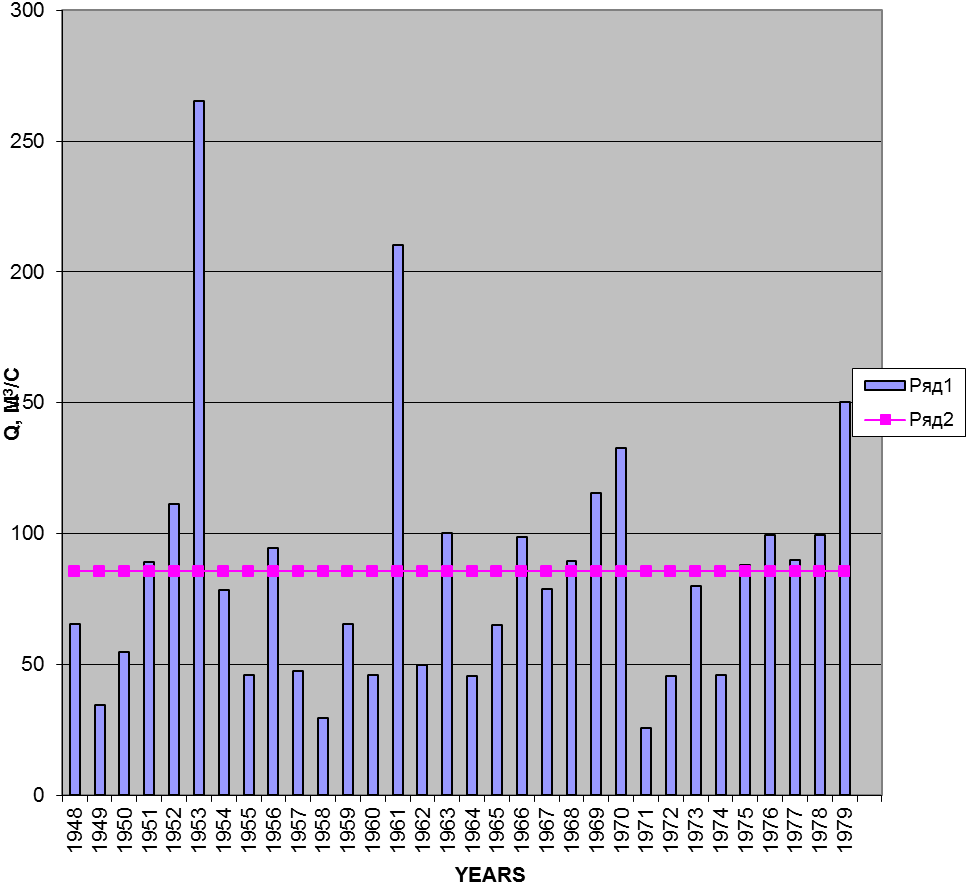
Рис 1.Номограмма среднегодового стока

Вывод: Года, в которых расход меньше нормы стока являются маловодными. А года, в которых расход больше – многоводными. Закономерность чередования много- и маловодных лет отсутствует, поэтому возможен только вероятностный прогноз.

Обработка ряда наблюдений: ранжируем ряд по убыванию и находим P.

Табл.№2 Ранжирование нормы стока по убыванию

№	Q	Р	№	Q	Р
	265,34	3,125		78,32	56,25
	210,22	6,25		65,32	59,375
	150,3	9,375		65,32	62,5
	132,54	12,5		64,98	65,625
	115,32	15,625		54,66	68,75
	111,28	18,75		49,85	71,875
	100,23	21,875		47,47
	99,34			45,88	78,125
	99,32	28,125		45,69	81,25
	98,77	31,25		45,69	84,375
	94,25	34,375		45,68	87,5
	89,95	37,5		45,68	90,625
	89,32	40,625		34,28	93,75
	89,21	43,75		29,32	96,875
	87,98	46,875		25,66
	78,93	53,125

После этого строим кривую обеспеченности (рис.2) и из заданного ряда выбираем расход, который ближе к расходу с 75%-ной обеспеченностью.

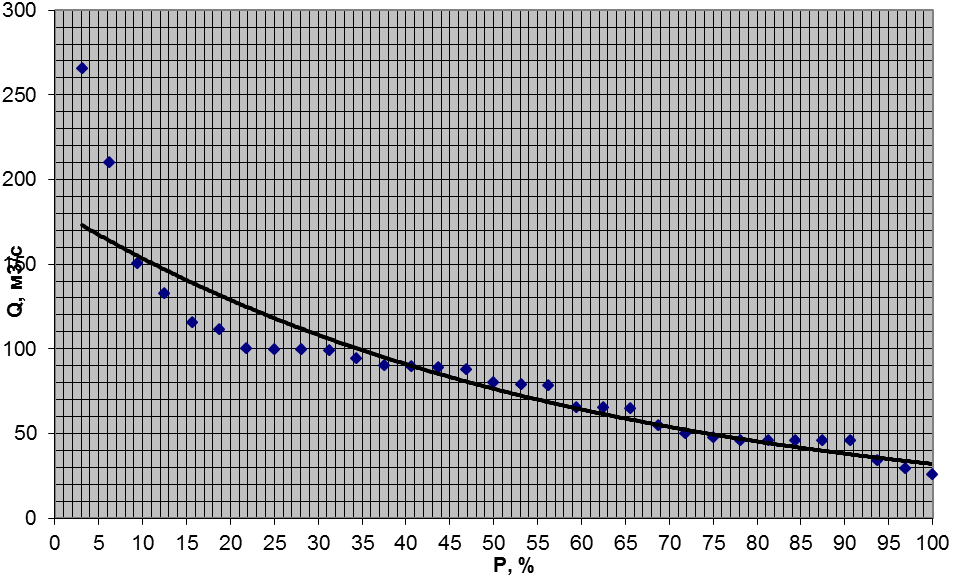
Рис 2.Кривая обеспеченности

Из гидрологического ежегодника выписываем среднемесячные расходы по данному году (расход в который максимально приближен к расходу Q_75%), строим таблицу распределения стока и определяем объем годового стока.

Q_75%=50

Q₁₉₆₂=49,85

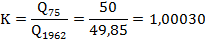
Табл.№3 Внутригодовое распределение стока на реке Пижма в 1962 году.

Месяц
Q1962	25,6	24,3	23,2	98,4	180,4	110,3	98,4	352,88	154,20	288,32	150,30	78,40
Qмес	25,67	24,37	23,27	98,7	180,94	110,63	98,7	353,94	154,66	289,19	150,75	78,64
tc	31,5*106
Wгод
Qср.г.	132,45

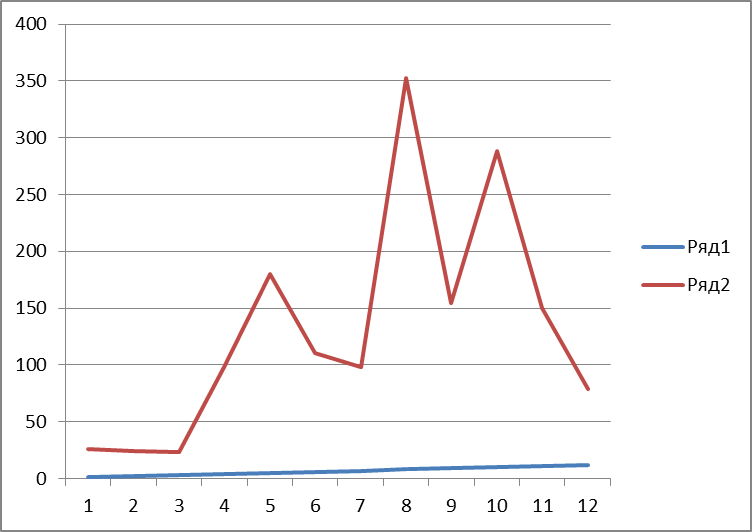
Строим гидрограф стока (рис3).

Лабораторная работа №1.

Движение потока на криволинейном участке русла.

Цель работы:

1. Используя микроманометр многодиапазонный (ММН), вычислить местные и средние на вертикали скорости в заданном створе;

2. Используя данные вычислений, построить эпюры распределения местных скоростей по вертикали, средней на вертикали продольной составляющей скорости течения по ширине русла и проанализировать изменение поля скоростей в заданном створе;

3. По вычисленным значениям построить эпюру удельного расхода и определить расход в заданном створе с использованием масштабного коэффициента;

4. Построить план криволинейного участка русла с эпюрами продольных скоростей и проанализировать изменение поля скоростей на подходе к излучине русла, в излучине и ниже по течению.

Порядок выполнения работы:

Лабораторная работа мы начали с изготовления плана криволинейного участка русла(, который мы вычертили на миллиметровке в результате обмеров модели в выбранном линейном горизонтальном масштабе (мы использовали масштаб 1:100). На плане мы показали створы и точками обозначили примерные вертикали в створах.

Мерной лентой измерили расстояния от уреза левого берега (УЛБ) до скоростных вертикалей l в каждом створе. Одновременно с помощью мерного щупа произвели промеры глубин воздушного потока h на вертикалях. Результаты промеров занесли в табл.7.

Затем включили вентилятор и в каждое отверстие створа ввели металлическую трубку микроманометра ММН и сняли отсчеты a по наклонной трубке в точках на каждой вертикали: на дне (а_дно), в середине скоростной вертикали (а_ср) и на поверхности воздушного потока (а_пов). Отсчеты занесли в табл.7.

Вследствие малости глубин можно считать, что указанные точки находятся от нижней поверхности стекла на расстояниях, соответствующих: первая – 0,8 h, вторая – 0,6 h, третья – 0.2 h.

В конце работы мы сняли показания с термометра и барометра.

Давление = 155

Температура = 20⁰С

Обработка результатов измерений:

1. Вычисляем местные скорости, т.е. скорости на вертикали в трех заданных точках, и результаты заносим в Табл.7.

2. Используя данные Табл.7, строим поперечный профиль заданного створа и эпюры распределения местных скоростей по вертикали (рис.8).

3. Вычисляем средние скорости на скоростных вертикалях по формуле трехточечного замера:

,

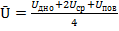где Ū – средняя скорость на скоростной вертикали; 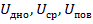– местные скорости соответственно на дне, середине, поверхности воздушного потока на вертикали.

4. Строим поперечный профиль заданного створа и эпюру средней на вертикали продольной составляющей скорости течения по ширине русла (рис.9).

5. Вычисляем удельные расходы q и по числовым значениям строим эпюру удельного расхода (см.рис.8).

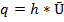
6. Определяем расход Q в заданном створе двумя методами и анализируем полученные числовые значения.

Первый метод.

Так как модель криволинейного участка русла закрыта стеклом, мощность вентилятора зафиксирована, то движение воздушного потока можно рассматривать как установившееся и расход вычислить по формуле

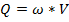
где ω – площадь живого сечения;

V – средняя скорость по живому сечению, которая определяется по формуле

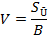
где S_{Ū –} площадь эпюры средних скоростей, м²/с; B – ширина русла в заданном створе.

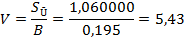
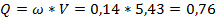
Второй метод (графический).

Как известно, расход жидкости связан с ее погонным расходом (удельным расходом) следующим выражением:

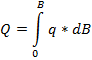
Но интеграл равен площади фигуры, ограниченной кривой q = f (B) и осью абсцисс с учетом масштабов чертежа. На рис.9 эта фигура заштрихована и является эпюрой удельного расхода.

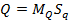
где M_Q – масштабный коэффициент расхода воздуха, определяющий величину расхода воздуха в каждой единице заштрихованной площади; S_q – площадь заштрихованной фигуры.

В качестве единицы площади берется площадь квадрата со стороной, равной линейной единице. Если в качестве этой единицы принять 1 см, то площадь квадрата равна 1см². Соответственно площадь заштрихованной фигуры S_q должна измеряться в см². По вертикали в каждом сантиметре площади S_q содержится M_q единиц удельного расхода, а по горизонтали – M_B линейных единиц, где M_q и M_B – масштабные коэффициенты соответственно удельного расхода и ширины. Отсюда в каждом квадратном сантиметре этой площади содержится расход воздуха, равный произведению этих масштабных коэффициентов:

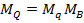
В расчетах линейный масштабный коэффициент нужно привести в соответствие с масштабным коэффициентом удельного расхода. Оба они должны показывать количество соответствующих единиц в одной линейной единице чертежа. Так, размерности масштабного коэффициента удельного расхода м²/с*см будет соответствовать размерность линейного масштабного коэффициента м/см. Таким образом, размерность масштабного коэффициента расхода воздуха M_Q будет м³/с*см².

Например, при использовании рекомендуемых масштабов для построения масштабный коэффициент удельного расхода M_q = 0,2, тогда линейный масштабный коэффициент M_B = 0,02.

7. На плане криволинейного участка русла строим эпюры продольных скоростей во всех створах и анализируем изменение поля скоростей на подходе к излучине русла, в излучине и ниже по течению.