Особенности функции в бесконечно удаленной точке
Под точкой 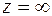 понимают абстрактную точку плоскости
понимают абстрактную точку плоскости  , окрестностью которой, является множество чисел
, окрестностью которой, является множество чисел  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , где
, где  любое действительное положительное число. Ряд Лорана функции
любое действительное положительное число. Ряд Лорана функции 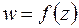 в окрестности точки
в окрестности точки 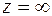 определяют с помощью замены переменной
определяют с помощью замены переменной  для функции
для функции  в окрестности точки
в окрестности точки  . Ряд Лорана в окрестности точки
. Ряд Лорана в окрестности точки 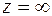 имеет вид
имеет вид
 ,
,
где  главная часть,
главная часть,
 правильная часть.
правильная часть.
Поведение функции в окрестности бесконечно удаленной точки дает возможность классифицировать ее особенности в этой точке.
Точка  называется устранимой особой точкой функции, если
называется устранимой особой точкой функции, если  , где
, где  .
.
Ряд Лорана в этом случае не содержит положительных степеней
 .
.
Точка 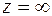 называется полюсом функции, если
называется полюсом функции, если  .
.
Если ряд Лорана в окрестности  содержит конечное число
содержит конечное число 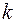 положительных степеней:
положительных степеней:
 ,
,
то точка 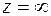 называется полюсом порядка
называется полюсом порядка 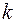 .
.
Точка 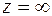 называется существенно особой для функции, если
называется существенно особой для функции, если  не существует.
не существует.
Ряд Лорана в этом случае содержит бесконечное число положительных степеней  .
.
Заметим, что точка 
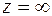 называется нулем порядка
называется нулем порядка  функции
функции  , если точка
, если точка  является нулем порядка
является нулем порядка  для функции
для функции  .
.
УПРАЖНЕНИЯ
95. Найти нули функции  и определить их порядки.
и определить их порядки.
Решение. Полагая  , получим
, получим  , откуда
, откуда  или
или  . Первое уравнение имеет корни
. Первое уравнение имеет корни  . Корнями второго уравнения являются числа
. Корнями второго уравнения являются числа  .
.
Итак, точки  нули функции
нули функции  .
.
Определим их порядки. Точки  нули 2-го порядка, так как они являются нулями 1-го порядка для функции
нули 2-го порядка, так как они являются нулями 1-го порядка для функции  и
и  . В самом деле, в силу (7.6) получаем
. В самом деле, в силу (7.6) получаем

Тогда  является нулями 1-го порядка данной функции
является нулями 1-го порядка данной функции  , так как
, так как

при  .
.
96. Найти особые точки функции и выяснить их характер:
а)  б)
б) 
в)  ; г)
; г)  .
.
Решение.а) Особая точка функции  (знаменатель дроби обращается в нуль). Легко видеть, что
(знаменатель дроби обращается в нуль). Легко видеть, что  , значит, согласно (7.2),
, значит, согласно (7.2),  полюс, причем 3-го порядка, так как по определению (7.3)
полюс, причем 3-го порядка, так как по определению (7.3)

 .
.
б) Изолированные особые точки  простые полюсы, так как для функции
простые полюсы, так как для функции  точки
точки  являются нулями 1-го порядка. Действительно,
являются нулями 1-го порядка. Действительно, 
 .
.
в) Особые точки:  .
.
Выясним их характер. Отметим, что в точке  обращается в нуль и числитель. Найдем предел функции при
обращается в нуль и числитель. Найдем предел функции при 

Следовательно, согласно (7.1), точка  является устранимой особой точкой. Точка
является устранимой особой точкой. Точка  простой полюс, так как для функции
простой полюс, так как для функции  эта точка является нулем 1-го порядка. В самом деле, функцию можно представить в виде
эта точка является нулем 1-го порядка. В самом деле, функцию можно представить в виде 
 , где
, где  аналитична в точке
аналитична в точке  и
и  . Точки
. Точки 
 также являются простыми полюсами, так как для функции
также являются простыми полюсами, так как для функции  они являются нулями 1-го порядка в силу того, что
они являются нулями 1-го порядка в силу того, что  .
.


г) в окрестности особой точки  для
для  имеет место следующее разложение:
имеет место следующее разложение:

 Главная часть лорановского разложения содержит бесконечно много членов. Следовательно, точка
Главная часть лорановского разложения содержит бесконечно много членов. Следовательно, точка  является существенно особой для функции
является существенно особой для функции  .
.
Замечание. Исследование функции  в существенно особой точке можно произвести лишь с использованием ряда Лорана.
в существенно особой точке можно произвести лишь с использованием ряда Лорана.
97.Определить характер особой точки 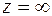 для функций:
для функций:
а)  б)
б) 
в)  г)
г) 
Решение.а) Точка  устранимая особая точка данной функции, так как
устранимая особая точка данной функции, так как 
б) точка  полюс функции
полюс функции  так как
так как  Порядок полюса равен порядку полюса функции
Порядок полюса равен порядку полюса функции  в точке
в точке 
 , функция же
, функция же  имеет в точке
имеет в точке  полюс 1-го порядка, так как функция
полюс 1-го порядка, так как функция  имеет в этой точке нуль 1-го порядка, в чем легко убедиться следующей проверкой:
имеет в этой точке нуль 1-го порядка, в чем легко убедиться следующей проверкой: 
 Таким образом,
Таким образом,  простой полюс данной функции.
простой полюс данной функции.
в) Разложим данную функцию в ряд Лорана в окрестности точки 

Так как главная часть ряда Лорана содержит конечное число положительных степеней  и старшая степень равна 3, то особая точка
и старшая степень равна 3, то особая точка 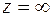 есть полюс 3-го порядка данной функции.
есть полюс 3-го порядка данной функции.
