Основные элементарные функции

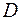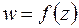Говорят, что на множестве точек плоскости задана функция , если каждой точке поставлено в соответствие одно (однозначная функция) или несколько (многозначная функция) значений комплексного переменного . Мы будем рассматривать только такие функции, для которых множества 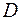и являются областями, причем 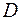называется областью определения, а областью значений функции .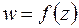

Задание функции комплексного переменного 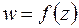равносильно заданию двух функций действительных переменных , :

, (3.1)

где , .

Это позволяет свести изучение функции комплексного переменного к изучению двух функций действительных переменных.

Геометрически заданную на D однозначную функцию 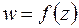можно рассматривать как отображение точек области D плоскости z в некоторую область G плоскости w. В этом отображении и проявляются свойства функции 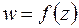(рис. 3.1).

Точки z, линии 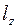, области 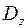называют прообразами точек 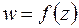, линий 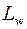и областей 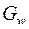соответственно, а w, 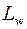, 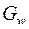называют образами при отображении .

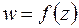Если в плоскости z кривая 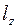задана неявным уравнением 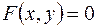, то для нахождения уравнения ее образа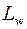 в плоскости w при отображении, осуществляемом функцией , достаточно

исключить x и y из уравнений

Рис.3.1

Если кривая 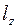задана параметрически уравнениями или , , то можно получить параметрические уравнения 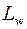, представив действительную и мнимую части как функции параметра t:

.

Комплексное число называется пределом функци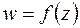и при , если для любого найдется такое, что для всех , удовлетворяющих неравенству , выполняется неравенство . В этом случае пишут .

Существование , где , равносильно существованию и , причем

.

Функция 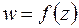называется непрерывной в точке 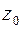, если она определена в точке 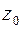и ее окрестности и , где конечное комплексное число.

Функция, непрерывная в каждой точке области D, называется непрерывной в этой области.

Для того, чтобы функция была непрерывна в точке , необходимо и достаточно, чтобы ее действительная и мнимая части были непрерывными функциями в точке .

Отметим, что понятия предела и непрерывности функции комплексного переменного вводятся аналогично, как это делается для функции действительного переменного. Свойства пределов и непрерывных функции действительного переменного остаются в силе для функций комплексного переменного.

Приведем некоторые элементарные функции комплексного переменного.

Дробно - рациональная функция

, . (3.2)

в частности, многочлен .

Показательная функция

, (3.3)

которая в отличие от функции действительного переменного является периодической функцией с периодом , т.е. .

3. Тригонометрические функции

, , (3.4)

, (3.5)

Для тригонометрических функций остаются в силе все формулы тригонометрии. В отличие от тригонометрических функций действительного аргумента модули функции и могут быть больше 1.

4. Гиперболические функции

, , (3.6)

, . (3.7)

Тригонометрические и гиперболические функции связаны между собой следующими соотношениями:

. (3.8)