Таблицы истинности и элементарные функции

Таблицы истинности и элементарные функции

1. Функции алгебры логики.

Алгебра логики задается двумя множествами: U и Р₂, где U – это множество всех высказываний, принимающих значения «истина» или «ложь», или любое другое множество, элементы которого могут принимать одно их двух значений или находиться в одном из двух состояний. Например, множество переключателей, каждый из которых может быть «включен» или «выключен», или множество электрических сигналов, поступающих на вход некоторого устройства, –«сигнал есть» или «сигнала нет» и т.п..

А множество Р₂ – это множество всех таких функций, которые принимают «истинностные» значения 0 или 1, если аргументы их пробегают те же значения. Алгебра логики занимается изучением свойств этих функций.

Истинностные функции называют также функциями алгебры логики, или булевыми функциями, или переключательными функциями.

Если f(x₁,x₂,…,x_n) – истинностная функция от n аргументов, т.е. f(x₁,x₂,…,x_n)Î Р₂, то она определяет отображение f: 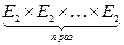® E₂. Нетрудно подсчитать число всех таких отображений.

Теорема 1.1.1. Число всех функций алгебры логики от n переменных равно 2²ⁿ.

Функция, принимающая значение, равное нулю на всех «энках», называется «противоречием».

Функция, принимающая значение, равное единице на всех «энках», называется «тавтологией».

«Энки», на которых функция принимает значение, равное единице, называются единичными «энками» или единичными наборами.

«Энки», на которых функция принимает значение, равное нулю, называются нулевыми «энками» или нулевыми наборами.

Способы задания функций алгебры логики

Укажем следующие 4 способа задания функций алгебры логики:

1) словесное описание;

2) табличное представление;

3) графическое изображение;

4) алгебраическое (в виде формулы).

Рассмотрим пример задания одной и той же функции от двух переменных каждым из перечисленных способов.

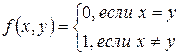– это словесное описание функции.

x	y	f(x,y)
			– табличное представление.

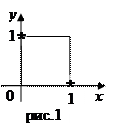
В графическом изображении единичные значения функции отмечаются некоторым способом, например «*», как на рисунке 1, а нулевые значения представляются неотмеченными вершинами единичного «куба» (в данном случае – квадрата).

Та же функция задается формулой: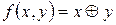

Таблицы истинности и элементарные функции

Рассмотрим таблицу значений функции от n переменных. Число строк в такой таблице будет равно числу всевозможных «энок», т.е. равно 2ⁿ. А число столбцов – числу переменных плюс единица, т.е. (n+1). При построении таблицы учтем, что каждую «энку» можно рассматривать как двоичное число, и выпишем их в порядке возрастания от 0 до 2ⁿ–1.

Таблица 1

x1	x2	x3	…	xn-1	xn	f(x1, x2, x3,…, xn-1, xn)
			…			f(0,0,0,…,0,0)
			…			f(0,0,0,…,0,1)
			…			f(0,0,0,…,1,0)
…	…	…	…	…	…	……………
			…			f(1,1,1,…,1,1)

В правом столбце таблицы 1 выпишем значения функции на соответствующих «энках». Такая таблица называется таблицей истинности или комбинационной таблицей. Последнее название объясняется тем, что с помощью неё можно описывать поведение логических схем, называемых также комбинационными схемами или схемами без внутренней памяти, на вход которых подается n сигналов, а выход является функцией входного набора сигналов и полностью определяется этим набором.

Приведем примеры таблиц истинности для элементарных функций алгебры логики, к которым относятся функции от одной и от двух переменных.

Заметим, что число функций от одной переменной равно 4 (см. таблицу 2), а от двух переменных – 16 (см. таблицу 3).

Таблица 2

x	g1(x)	g2(x)	g3(x)	g4(x)

В таблице 2 функция g₁(x) – это константа ноль или «противоречие».

Функция g₂(x) – «тождественная функция x».

Функция g₃(x) – «отрицание x», обозначается « 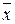» или « ».

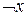Функция g₄(x) – константа единица или «тавтология».

Таблица 3

x

y

f1

f2

f3

f4

f5

f6

f7

f8

f9

f10

f11

f12

f13

f14

f15

f16

Обозначение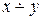

&

x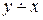

y

Å

Ú

¯

º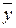

y®x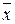

x®y

|

В таблице 3 приведены обозначения элементарных функций. Эти обозначения (символы) принято называть пропозициональными связками или символами логических операций. Укажем также их названия, способы вычисления и прочтения.

Функция f₁(x,y) – это так же, как и в таблице 2, константа ноль или «противоречие».

Функция f₂(x,y)=x&y – «конъюнкция» х и у или «логическое умножение». Читается: «х и у». Значения этой функции можно получить простым умножением значений её аргументов или как наименьшее из значений аргументов, т.е. f₂(x,y) = x&y = x×y = min(x, y).

Функции f₃(x,y)= 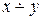и f₅(x,y)= 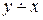– это «условное вычитание» у из х, и х из у,соответственно. Их значения можно получить по правилу: 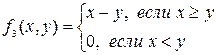и .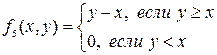

Функции f₄(x,y)=х и f₆(x,y)=у – как и в таблице 2, «тождественная функция x» и «тождественная функция у» соответственно.

Функция f₇(x,y)=хÅу – «сложение по модулю 2» или «исключающее или». Значения этой функции равны остатку от деления на 2 суммы её аргументов.

Функция f₈(x,y)=хÚу – «дизъюнкция» х и у или «логическое сложение». Читается: «х или у». Значения этой функции можно получить как наибольшее из значений аргументов, т.е. f₂(x,y) = xÚy = max(x, y).

Функция f₉(x,y)=х¯у – «стрелка Пирса» или «отрицание дизъюнкции» или «конъюнкция отрицаний». Последние два названия обусловлены правилом, по которому получаются значения этой функции.

Функция f₁₀(x,y)=хºу – «эквиваленция». Читается: «х эквивалентно у». Значения этой функции получаются по правилу: .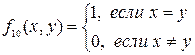

Функции f₁₁(x,y)= 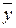и f₁₃(x,y)= 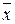– это так же, как и в таблице 2, «отрицание у» и «отрицание х» соответственно.

Функции f₁₂(x,y)= y®x и f₁₄(x,y)= x®y – это так называемая «импликация». Для чтения выражения x®y можно использовать фразу «х влечет у» или «если х, то у». Значения x®y получаются как ответ на вопрос «х меньше, либо равно у?». При этом положительный ответ записывается «1», а отрицательный – «0».

Функция f₁₅(x,y)= y | x – «штрих Шеффера» или «отрицание конъюнкции» или «дизъюнкция отрицаний». Последние два названия обусловлены правилом, по которому получаются значения этой функции.

Последняя функция в таблице 3 – это так же, как и в таблице 2, константа единица или тавтология.