Типы задач, решаемые способом преобразования плоскостей проекций

Путем преобразования проекций возможно решение следующих задач:

1. Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций.

2. Определение расстояния от точки до прямой.

3. Определение расстояния между параллельными прямыми.

4. Определение расстояния между скрещивающимися прямыми.

5. Определение величины двугранного угла.

6. Определение расстояния от точки до плоскости.

7. Определение расстояния между параллельными плоскостями.

8. Определение истинной величины плоской фигуры.

9. Определение угла наклона прямой и плоскости.

10. Определение углов наклона плоскости к плоскостям проекций и т.п.

Пример:

Определить расстояние от точки D до плоскости АВС (рис. 39). Для определения искомого расстояния плоскость АВС преобразуем в проецирующую, для этого в ней проведем горизонталь (h) и новую плоскость П₄ поставим перпендикулярно h, а значит, Х_1,4 перпендикулярно проекции горизонтали (h₁), таким образом, плоскость АВС станет перпендикулярной плоскости П₄ Искомое расстояние - ( D₄K₄ ) - величина перпендикуляра, опущенного из . D₄ на линию А₄В₄С₄ (проекцию плоскости АВС на плоскость П₄).

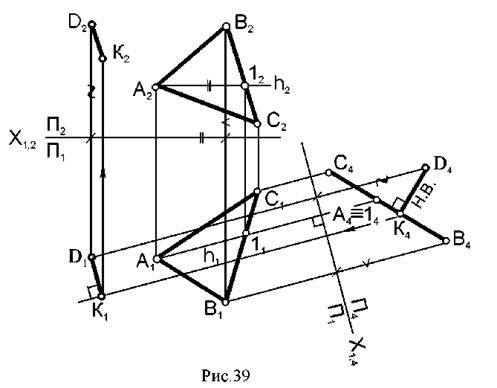
Вопросы для самопроверки.

1. Какие существуют способы преобразования проекций?

2. В чем сущность изображения проекций способом замены плоскостей проекций?

3. Перечислите 4 основные задачи, решаемые методом замены плоскостей проекций.

4. Какие типы задач можно решить способом замены плоскостей проекций?

Лекция 6. Способ вращения.

Сущность способа.

Сущность способа вращения состоит в изменении положения объекта, заданного на эпюре, таким образом, чтобы определенные его элементы заняли относительно плоскостей проекций частное положение и проецировались без искажения.

Начиная преобразование этим способом, надо подготовить аппарат вращения: ось, центр и радиус вращения.

По положению оси вращения различают несколько видов этого способа.

Вращение вокруг оси, перпендикулярной плоскости проекций. При вращении точки в пространстве вокруг оси, перпендикулярной горизонтальной плоскости проекций, проекции точки перемещаются так: горизонтальная – по окружности, фронтальная – по прямой, параллельной оси проекций (или перпендикулярной оси вращения) (рис.40).

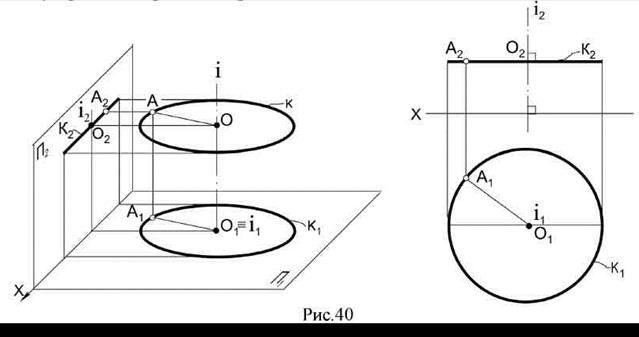
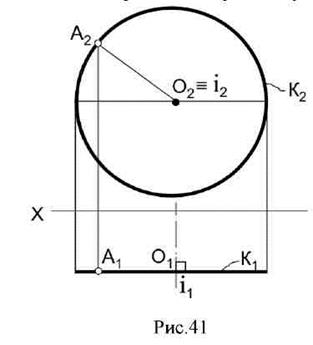
Если ось вращения перпендикулярна фронтальной плоскости проекций, то на эпюре получается обратная картина (рис.41).

Чтобы повернуть вокруг оси прямую линию, достаточно вращать ее точки на один и тот же угол. При вращении плоскости следует вращать определяющие ее элементы: три точки, прямую и точку и т.д. Этим способом удобно определять натуральную величину отрезка прямой и угол наклона ее к плоскости проекций, при этом ось вращения рационально провести через одну из точек прямой линии, чтобы избежать лишних построений.

Определить натуральную величину отрезка прямой АВ (рис. 42)

Чтобы прямая проецировалась в натуральную величину, она должна располагаться параллельно какой - либо плоскости проекций, а значит, одна ее проекция должна быть параллельна оси проекций:

АВ || П₁; Â₂B₂ || ОХ; ось вращения проходит через точку В; Â ₁ B ₁ - натуральная величина АВ.

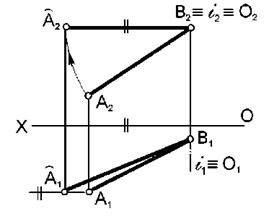
Рис. 42