Классификация поверхностей

По виду образующей:

1. Линейчатые поверхности - с прямолинейной образующей.

2. Нелинейчатые - с криволинейной образующей.

По закону движения образующей: (т.е. по направляющей)

1. Поверхности вращения.

2. Винтовые поверхности.

3. Поверхности с плоскостью параллелизма (поверхности Каталана).

Линейчатые поверхности.

Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим. Возьмем в пространстве три кривые линии l.

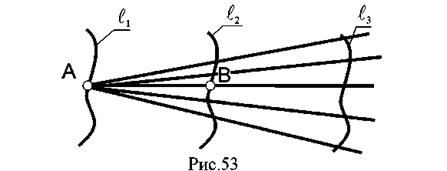
Пусть прямая движется так, что в любом своем положении она пересекает все три кривые l₁ l₂, l₃, тогда при своем движении они описывают линейчатую поверхность (рис. 53).

Выберем на направляющей l₁ точку А. Через нее мы сможем провести бесчисленное множество прямолинейных образующих, пересекающих направляющую l₃. Этим самым определяется коническая поверхность с вершиной в точке А. В какой - то момент образующие пересекут линию l₂ - это точка В, в которой коническая поверхность пересечет линию l₂. В зависимости от вида направляющих получаются различные поверхности.

Поверхности с одной направляющей:

1. Коническая - образуется движением прямой линии l (образующей) по некоторой кривой линии m и имеющей неподвижную точку S (рис. 54).

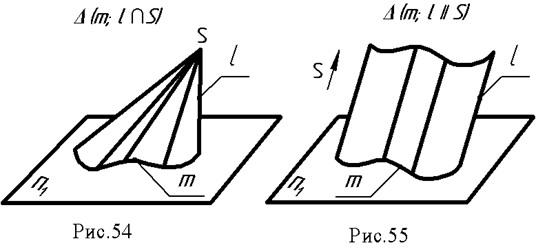
2. Цилиндрическая поверхность образуется движением прямой l(образующей) по некоторой кривой т параллельно самой себе или имеющей постоянное направление S∆(т,1|| S) (рис. 55).

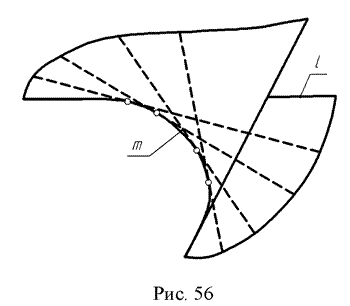
3. Торсовая поверхность образуется движением прямой l, касающейся во всех своих положениях некоторой пространственной направляющей кривой т, называемой ребром возврата ∆ (т,l) (рис.56).

4. Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей.

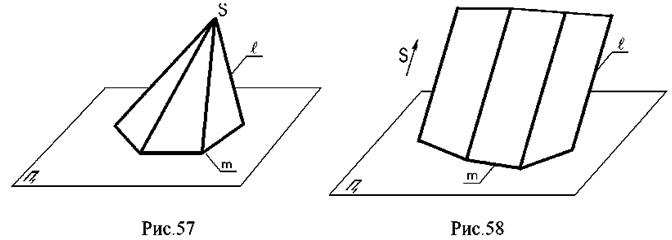
Если направляющая т ломаная, а все образующие lпересекаются в одной точке, такая поверхность называется пирамидальной (рис. 57); если все образующие параллельны - поверхность называется призматической (рис. 58).

Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников. Отсеки плоскостей называются гранями, а линии их пересечения - ребрами. Точки пересечения ребер называются вершинами.

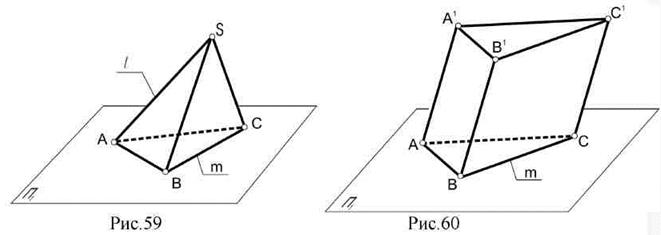
Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой (рис.59).

Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно параллельными ребрами - призма (рис.60).

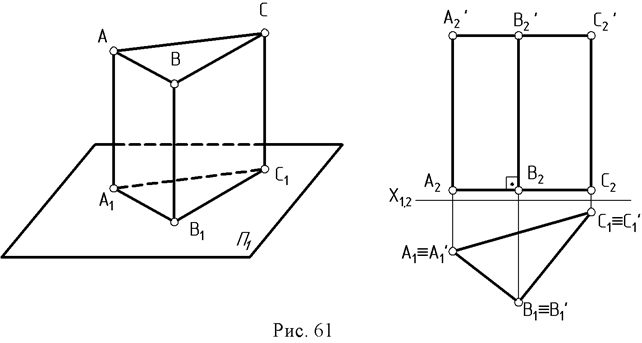
Если ребра призмы перпендикулярны основанию, гранник называется проецирующей призмой (рис.61).

Вопросы для самопроверки.

1. Как классифицируются кривые линии?

2. Какие точки кривой относят к характерным?

3. Укажите основные способы задания поверхностей.

4. Что называют каркасом поверхности?

5. Что называют определителем поверхности?

6. Как классифицируются поверхности?

7. Как образуются коническая и цилиндрическая поверхности?

8. Как образуются пирамидальная и призматическая поверхности?