С помощью единичной функции соответствие (1.3) можно записать в виде
 .
.
Полагая здесь  , снова получаем соответствие (1.2)
, снова получаем соответствие (1.2)

которое можно записать и так:
 .
.
2. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ ИЗОБРАЖЕНИЯ
И ЕДИНСТВЕННОСТИ ОРИГИНАЛА
Требования 1, 2, 3 наложены на функцию  неслучайно. Только при таких условиях несобственный интеграл (1.1) сходится и, следовательно, определяет некоторую функцию
неслучайно. Только при таких условиях несобственный интеграл (1.1) сходится и, следовательно, определяет некоторую функцию  . Установлено, что условия 1-3, которые удовлетворяют оригиналы, являются достаточными условиями сходимости интеграла Лапласа. Но если
. Установлено, что условия 1-3, которые удовлетворяют оригиналы, являются достаточными условиями сходимости интеграла Лапласа. Но если  является оригиналом, то возникает вопрос, в какой области комплексной плоскости
является оригиналом, то возникает вопрос, в какой области комплексной плоскости 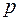 интеграл Лапласа сходится, т.е. существует изображение
интеграл Лапласа сходится, т.е. существует изображение  . Именно с таким вопросом мы столкнулись и дали на него ответ при отыскании изображения единичной и показательной функции, исходя из его определения. Ответ на эти вопросы дает следующая теорема.
. Именно с таким вопросом мы столкнулись и дали на него ответ при отыскании изображения единичной и показательной функции, исходя из его определения. Ответ на эти вопросы дает следующая теорема.
Теорема (существования изображения).Если функция  - является оригиналом, то ее изображение
- является оригиналом, то ее изображение  определено для всех значений комплексного переменного
определено для всех значений комплексного переменного 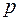 , удовлетворяющих условию
, удовлетворяющих условию  , т.е. в полуплоскости
, т.е. в полуплоскости  , где
, где  показатель роста функции
показатель роста функции  , и является аналитической функцией в этой области.
, и является аналитической функцией в этой области.
 Рис.2.1 Рис.2.1 | Геометрически теорему можно истолковать следующим образом. Если на комплексной плоскости 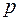 через точку через точку  действительной оси действительной оси  (рис.2.1) провести прямую параллельно мнимой оси (рис.2.1) провести прямую параллельно мнимой оси  , то интеграл (1.1) сходится везде в области, расположенной правее от этой прямой, причем функция , то интеграл (1.1) сходится везде в области, расположенной правее от этой прямой, причем функция  является аналитической в ней. является аналитической в ней. |
Доказательство.Для доказательства первой части теоремы достаточно установить абсолютную сходимость интеграла Лапласа в области  . Известно, что абсолютная величина интеграла не больше интеграла от абсолютной величины подынтегральной функции, т.е.
. Известно, что абсолютная величина интеграла не больше интеграла от абсолютной величины подынтегральной функции, т.е.
 .
.
По условию  оригинал и, следовательно, выполняется условие 3, согласно которому
оригинал и, следовательно, выполняется условие 3, согласно которому
 .
.
Кроме того,


Поэтому
 .
.
Тогда
 (2.1)
(2.1)
 . Отсюда в силу признака сравнения вытекает сходимость интеграла Лапласа, а значит, существование изображения
. Отсюда в силу признака сравнения вытекает сходимость интеграла Лапласа, а значит, существование изображения  для тех значений р, у которых
для тех значений р, у которых  .
.
Доказательство второй части теоремы, а именно аналитичности функции  в полуплоскости
в полуплоскости  сложнее и здесь не будет проведено. Оно основано на свойствах равномерно сходящихся интегралов.
сложнее и здесь не будет проведено. Оно основано на свойствах равномерно сходящихся интегралов.
Следствие (поведение изображения, на бесконечности). Если точка р стремится в бесконечность так, что  , то изображение
, то изображение  .
.
Справедливость этого утверждения непосредственно следует из неравенства (2.1). Действительно,  , но
, но  , а поэтому
, а поэтому  .
.
Приведенные теорема и следствие позволяют высказать следующее суждение: не всякая функция  комплексного переменного р может служить изображением некоторого оригинала
комплексного переменного р может служить изображением некоторого оригинала  . Из аналитичности функции
. Из аналитичности функции  в полуплоскости
в полуплоскости  следует, что все особые точки
следует, что все особые точки  должны лежать левее прямой
должны лежать левее прямой  (или на самой прямой). По этой причине функция
(или на самой прямой). По этой причине функция  не является изображением: она имеет бесконечное число полюсов
не является изображением: она имеет бесконечное число полюсов 
 на оси
на оси  . Функция
. Функция  также не является изображением, так как
также не является изображением, так как  не стремится к нулю, когда
не стремится к нулю, когда  .
.
Обсудим полученные в п.1.2 операционные соотношения (1.2) и (1.3) в связи с приведенной теоремой. Правая часть формул–функция  определена и аналитична при всех значениях р, кроме
определена и аналитична при всех значениях р, кроме  , где она имеет полюс.
, где она имеет полюс.
