ЛЕКЦИЯ 9. Линейная пространственная фильтрация
Пространственная фильтрация изображения f (x, y), x Î[0,(N − 1)], y Î[0,(M − 1)] позволяет применять фильтры с КИХ. Поскольку в изображении понятия прошлого и будущего времени становятся условными, мы можем использовать амплитуды отсчетов как в направлении увеличения индексов, так и в направлении уменьшения индексов. Пространственная фильтрация выполняется как операция двумерной свертки импульсной характеристики фильтра h(s,t) с изображением f (x, y), где s – координата характеристики в горизонтальном направлении вдоль оси x, s Î [−n / 2,n / 2], t – координата характеристики в вертикальном направлении вдоль оси y, t Î [−m/ 2,m/ 2]:
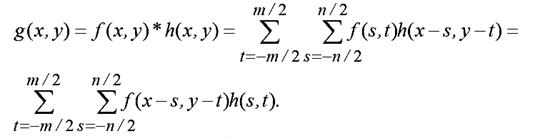
Прямоугольная область размером n × m, на которой задана импульсная характеристика, называется маской или ядром фильтра. Рассмотрим, как соотносятся координаты изображения и импульсной характеристики фильтра на примере.
Пусть m =3, n =3. Элементы импульсной характеристики фильтра и соответствующей области изображения представлены на рисунке 9.1. Начало координат фильтра устанавливается в центр импульсной характеристики, как показано на рисунке 9.1. Отсчеты импульсной характеристики отражаются относительно начала координат (что равносильно повороту маски на 180°), и центр маски смещается в положение (x, y).
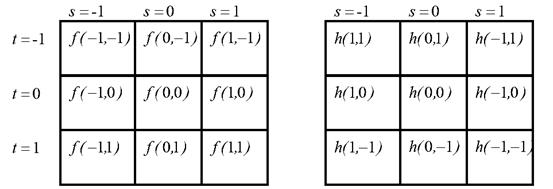
Рисунок 9.1 – Положение отсчетов импульсной характеристики при свертке с изображением f(x, y)
Отклик фильтра g(x, y) вычисляется как сумма произведений отсчетов изображения на соответствующие отсчеты повернутой импульсной характеристики. Эта операция выполняется для каждого отсчета изображения.
Если импульсная характеристика фильтра симметрична, то есть h( s,t ) = h( −s,−t ), то вместо свертки можно выполнять корреляцию:
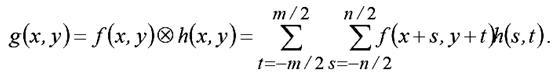
Эта операция не требует отражения импульсной характеристики, а представляет собой вычисление в скользящей по изображению маске фильтра произведений отсчетов изображения на соответствующие коэффициенты фильтра и их суммирование (в соответствии с рисунком 9.2).
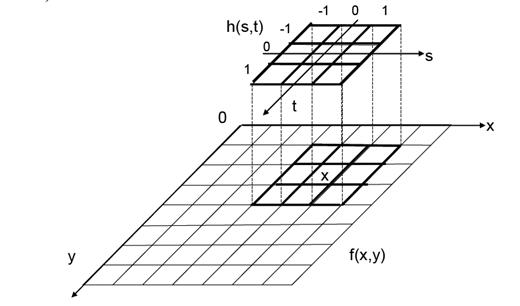
Рисунок 9.2 – Корреляция изображения f(x, y) с маской h(s, t)
Для обработки краевых эффектов необходимо увеличить изображение по строкам и столбцам на n/2 отсчетов слева и справа и на m/2 отсчетов сверху и снизу. При этом расширение может выполняться разными способами: дополнением нулями, повторением граничных элементов, периодическим повторением ( x mod N , y mod M ) или зеркальным отражением граничных элементов. Размер выходного изображения при этом сохраняется равным размеру входного изображения.
При построении линейных КИХ фильтров часто используют непараметрический подход. Линейные сглаживающие фильтры. Для уменьшения шумов широко применяются НЧ фильтры, поскольку шум представляет собой ВЧ сигнал. В частности, для НЧ фильтрации применяется усреднение сигнала в маске, например, при n=m=3:
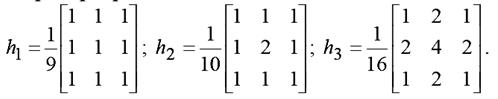
Нормировка необходима для того, чтобы привести значения отклика фильтра к диапазону входных данных. Нормирующий коэффициент определяется из условия равенства единице суммы всех коэффициентов КИХ в соответствии с уравнением:
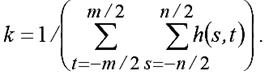
Линейная фильтрация широко применяется при подавлении шумов в изображении, для компенсации неравномерности чувствительности, создания эффектов размытия изображений.
