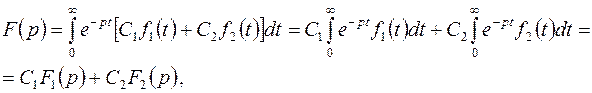Однако, пользуясь теоремой существования изображения, мы можем лишь утверждать, что функция представима интегралом Лапласа
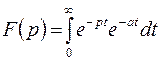 ,
,
только при  ,
,  и в полуплоскости
и в полуплоскости 
 не будет иметь особых точек: все они оказываются лежащими или левее прямой
не будет иметь особых точек: все они оказываются лежащими или левее прямой  , или на ней самой.
, или на ней самой.
Таким образом, теорема существования устанавливает условия, при которых функции  действительного переменного ставятся в соответствие единственная функция
действительного переменного ставятся в соответствие единственная функция  комплексного переменного – ее изображение. Будет ли это соответствие взаимооднозначным. Другими словами, будет ли каждому изображению (некоторой функции комплексного переменного) соответствовать единственный оригинал. Ответ на этот вопрос дан в следующей теореме, которую мы приведем без доказательства.
комплексного переменного – ее изображение. Будет ли это соответствие взаимооднозначным. Другими словами, будет ли каждому изображению (некоторой функции комплексного переменного) соответствовать единственный оригинал. Ответ на этот вопрос дан в следующей теореме, которую мы приведем без доказательства.
Теорема (единственности оригинала).Если  является изображением двух оригиналов
является изображением двух оригиналов 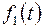 и
и 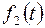 , то эти оригиналы совпадают во всех точках, в которых они непрерывны.
, то эти оригиналы совпадают во всех точках, в которых они непрерывны.
Различные разрывные функции могут иметь одинаковое изображение.
3. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
При практическом применении преобразования Лапласа операции выполняются не над заданными функциями, а над их изображениями. Весь процесс преобразования Лапласа можно представить себе как перевод с одного языка на другой. Как каждому слову одного языка соответствует определенное слово другого языка, точно так же при преобразовании Лапласа каждой функции пространства оригиналов соответствует определенная функция в пространстве изображений. Роль словаря, необходимого для перевода с одного языка на другой, играет таблица соответствий между оригиналами и изображениями. Два соответствия мы уже получили в п.1.2, пользуясь непосредственно определением изображения функции. Для того, чтобы перевести целое предложение, недостаточно знать перевод отдельных слов; необходимо еще знать, как грамматические образования одного языка передаются на другом языке. В применении к преобразованию Лапласа это означает следующее: если над функцией, например, в пространстве оригиналов производится какая-либо операция, скажем, дифференцирование или интегрирование, то в пространстве изображений этой операции отвечает вполне определенная другая операция. Или если в пространстве оригиналов несколько функций комбинируются одна с другой, например, перемножаются, то в пространстве изображений такой комбинации отвечает определенная другая комбинация.
Таким образом, необходимо знать не только изображение отдельных функций, но и правила отображения выполняемых над ними операций. Правила, которые ниже будут установлены, иначе свойства преобразования Лапласа позволят найти изображения для многих функций, не вычисляя каждый раз интеграл Лапласа, что вообще говоря, весьма затруднительно, и таким образом составить таблицу соответствий между оригиналами и изображениями.
3.1. Некоторые основные теоремы операционного исчисления
3.1.1. Теорема линейности. Для любых действительных или комплексных чисел С и С2
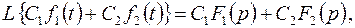 (3.1)
(3.1)
т.е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.
Доказательство.Пусть оригинал  представлен линейной комбинацией функций
представлен линейной комбинацией функций 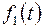 и
и 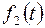 :
: 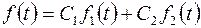 .И пусть
.И пусть 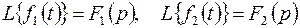 , а
, а 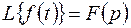 . Тогда по определению изображения найдем
. Тогда по определению изображения найдем