Взаимная принадлежность точки, прямой и плоскости

УЧЕБНОЕ ПОСОБИЕ

по курсу «Начертательная геометрия»

МОДУЛЬ №2

Тольятти 2007

УДК 514.18(076)

ББК 22.15.3

Н36

Рецензент:

к.т.н., доцент А.Г. Егоров (ТГУ).

Н36Начертательная геометрия. Модуль №2 : учеб.-метод. Пособие / сост. Т.А. Варенцова, Г.Н. Уполовникова. – Тольятти : ТГУ, 2007.- 48 с.

Содержит полный теоретический материал для успешного освоения студентами курса «Начертательная геометрия». Учебный материал разбит на 4 модуля. Каждый модуль является логически завершенной частью, заканчивается контрольными вопросами и тестом с ответами для самоконтроля студента.

Для студентов технических специальностей высших учебных заведений

Рекомендовано к изданию методической комиссией автомеханического института Тольяттинского государственного университета

© Т.А. Варенцова, Г.Н. Уполовникова,

Составление, 2007

© Тольяттинский государственный

Университет, 2007

Содержание

Комплексный чертёж плоскости и поверхности. 4

Задание плоскости на комплексном чертеже. 4

Взаимная принадлежность точки, прямой и плоскости. 5

Плоскости частного положения. 7

Проецирующие плоскости. 8

Горизонтально проецирующая плоскость. 8

Фронтально проецирующая плоскость. 8

Плоскости уровня (дважды проецирующие) 9

Горизонтальная плоскость уровня. 9

Фронтальная плоскость уровня. 10

Особые линии плоскости. 11

Горизонталь плоскости. 11

Фронталь плоскости. 12

Линия наибольшего наклона плоскости. 14

Прямая, параллельная плоскости. 18

Взаимная параллельность плоскостей. 19

Справочный материал. 20

Примеры изображения плоскостей общего и частного положения, заданные геометрическими фигурами. 20

Плоскости общего положения. 20

Горизонтально проецирующие плоскости. 21

Фронтально проецирующие плоскости. 21

Горизонтальные плоскости уровня. 21

Фронтальные плоскости уровня. 22

Контрольные вопросы.. 22

Тест № 1. 23

Задание поверхности на комплексном чертеже. 23

Определитель поверхности. 24

Очерк проекции поверхности. 24

Классификация поверхностей. 25

Алгоритм конструирования поверхности. 26

Задание линейчатых поверхностей на комплексном чертеже. 28

Развертывающиеся поверхности. 28

Многогранные поверхности. 28

Комплексный чертеж пирамидальной поверхности. 29

Комплексный чертеж призматической поверхности. 34

Проецирующая призма. 36

Задание кривых линейчатых поверхностей. 37

Задание конической поверхности общего вида на комплексном чертеже. 38

Задание цилиндрической поверхности общего вида на комплексном чертеже. 40

Неразвертывающиеся линейчатые поверхности с двумя направляющими. 42

Цилиндроид. 44

Коноид. 47

Гиперболический параболоид. 49

Поверхности вращения. 50

Комплексный чертеж поверхности вращения общего вида. 51

Поверхности вращения второго порядка. 55

Цилиндр вращения. 55

Конус вращения. 55

Сфера. 56

Поверхности вращения второго порядка. 58

Эллипсоид вращения. 58

Эллипсоид сжатый. 59

Эллипсоид вытянутый. 59

Параболоид вращения. 59

Гиперболоид вращения. 60

Алгоритм построения главного меридиана однополостного гиперболоида, 63

Тор- поверхность вращения 4 порядка. 66

Винтовые поверхности. 73

Прямой геликоид. 74

Наклонный геликоид. 74

Контрольные вопросы.. 78

Ответы на тест - № 4. 78

Справочный материал. 79

Задание плоскости на комплексном чертеже. 79

Задание поверхности на комплексном чертеже. 79

Комплексный чертёж плоскости и поверхности

В данном модуле вы познакомитесь с различными видами поверхностей и их модификациями, способами задания их на комплексном чертеже, особенностями построения. Узнаете, что простейшая поверхность - это плоскость.

Задание плоскости на комплексном чертеже

«Поверхность есть то, что имеет только длину и ширину»

(Евклид «Начала», 4 век до н.э., книга 1, определение 5.)

Как вы думаете?

1. Не дана ли в "Началах" трактовка поверхности слишком упрощенно?
2. Какая фигура в современном понимании имеет "только длину и ширину"?
3. Безразмерна ли плоскость, или она имеет границы?
4. Можно ли задать плоскость пространственными линиями?

Плоскость является частным случаем поверхности - это двумерная геометрическая фигура, она имеет только длину и ширину, и не имеет толщины. Обозначается прописными буквами греческого алфавита. Плоскость - это множество точек, но определяется она тремя точками (напомним, что прямую линию определяют две точки).

Плоскость можно задать на чертеже:

1. Тремя точками: S(А, В, С);

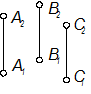
1. Прямой и точкой, не лежащей на данной прямой: Г(а, В);

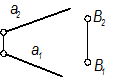
Двумя параллельными прямыми: D(с|| а);

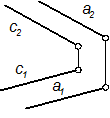
1. Двумя пересекающимися прямыми: F(m Ç n);

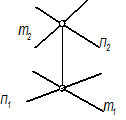
1. Любой плоской фигурой: L(АВС);

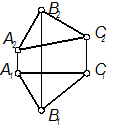
1. Своей главной проекцией: W(W­₁);

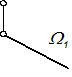
1. Линией наибольшего наклона плоскости Q (g₁ ,g₂);

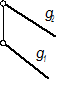
Рис. 2-1

Плоскости бывают общего и частного положения

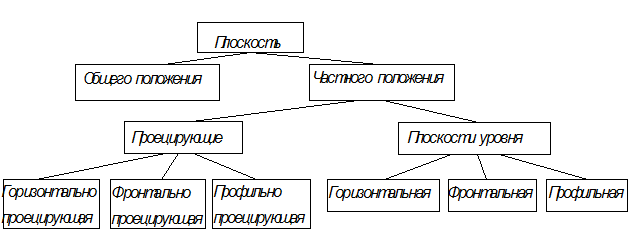
Рис. 2-2

Если плоскость не перпендикулярна ни одной из плоскостей проекций,

то она называется плоскостью общего положения

Примеры чертежа плоскости общего положения см. варианты 1 - 5; 7 (рис. 2-1).

Взаимная принадлежность точки, прямой и плоскости