Пересечение гранной поверхности с плоскостью
Результатом пересечения гранной поверхности плоскостью является плоская ломаная линия; вершины этой ломаной можно определить как пересечение данной плоскости с ребрами гранной поверхности.
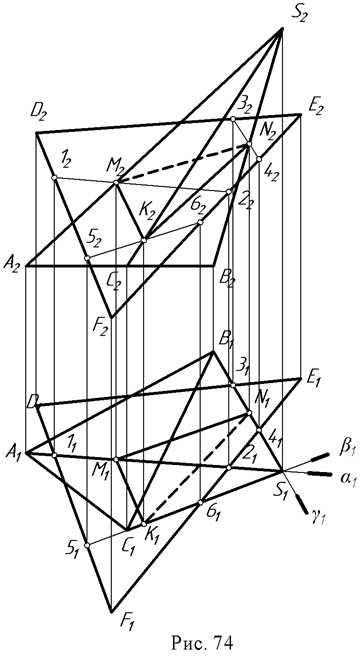
Пример: Определить линию пересечения пирамиды SАВС с плоскостью ∆DEF (рис. 74). Находят точки пересечения ребер пирамиды с плоскостью. Например, через ребро SА (S1A1) проведена горизонтально - проецирующая плоскость α (α1), которая пересечет плоскость ∆DEF по линии 1-2 (11 - 21 12 - 22) на фронтальной проекции отмечена точка М (М2) - как пересечение S2A2 с линией (12 - 22); проекция М1 лежит на проекции S1A1. Такие построения выполнены с каждым ребром пирамиды. Получены точки К (К1 К2) и N (N1 ,N2). Соединив их, следует определить видимость.
Вопросы для самопроверки
1.Укажите общую схему определения точек линии пересечения поверхности плоскостью общего положения.
2.Укажите общую схему определения точек линии пересечения поверхности проецирующими плоскостями.
3.Какие точки линии пересечения поверхности с плоскостью называют опорными (характерными)?
4.Укажите условия, при которых в сечении конуса вращения плоскостью, получаются окружность, эллипс, гипербола, парабола, пересекающиеся прямые?
5.Как построить высшую и низшую точки конического сечения?
6.Как построить линию пересечения гранной поверхности с плоскостью?
Лекция 10. Пересечение прямой с поверхностью.
Общие положения
Прямая линия может пересекать поверхность в одной, двух и более точках, может касаться ее. Если прямая не имеет общих точек с поверхностью, это означает, что она не пересекает поверхность. Этапы решения этой задачи аналогичны описанному ранее алгоритму на определение точки пересечения прямой с плоскостью.
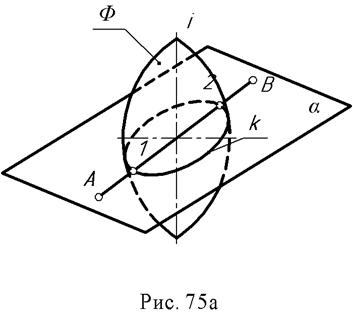
Через прямую АВ проводят вспомогательную плоскость – посредник α (рис. 75а).
Находят линию пересечения поверхности с плоскостью α – (к).
Отмечают точки пересечения линии АВ с линией К, точки 1 и 2.
Количество точек пересечения прямой с поверхностью определяет порядок последней.
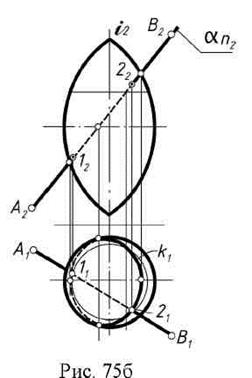
Решение задачи на комплексном чертеже (рис. 75б).
Через прямую АВ проводят плоскость α Ö П2; линию к строят, как это было описано выше.
Отмечают точки пересечения линии к1 с А1В1 – точки 11 и 21 и находят их на фронтальной проекции.
В качестве плоскости – посредника можно использовать и плоскость общего положения. Это применяют в том случае, когда заданная поверхность линейчатая, тогда при построении линии сечения вспомогательной плоскости – посредника с поверхностью избегают построения сечения как кривой линии.