Гиперболический параболоид

Г (m, n, Y) а(а₂) Î Г, а₁ = ?

Закон каркаса: l Ç m, l Ç n, l || Y

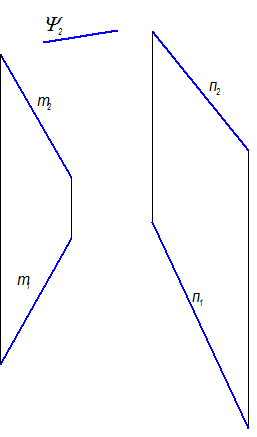
Рис. 2-74

Задать проекции элементов определителя m(m₁, m₂); n(n₁, n₂).

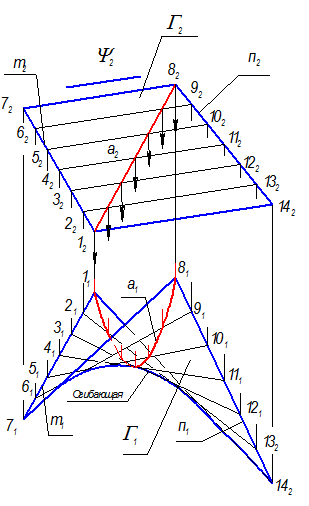
Рис 2-75

Поверхности вращения

Поверхности вращения широко распространены в технике - это связано с простотой их обработки.

Поверхность вращения образует какая - либо линия - образующая (l) при ее вращении вокруг неподвижной оси (i).

Образующая (l) может быть как прямая, так и кривая линия - плоская или пространственная.

Свойства поверхности вращения:

Каждая точка образующей (l) при вращении вокруг оси опишет окружность с центром на оси, плоскость которой перпендикулярна оси. Эти окружности называются параллелями. Все параллели параллельны между собой.

Самая большая параллель называется экваториальной (экватор) (рис. 2-76)- точка (В) максимально удалена от оси; самая малая параллель называется горловой (горло), у некоторых поверхностей вращения отмечают верхнюю (С) и нижнюю (D) параллели (часто они являются линиями обреза поверхности).

Линии, которые получаются в сечении поверхности вращения плоскостями, проходящими через ось, называются меридианами. Все меридианы равны между собой. Каждый меридиан рассекается этой плоскостью на два полумеридиана (правый и левый).

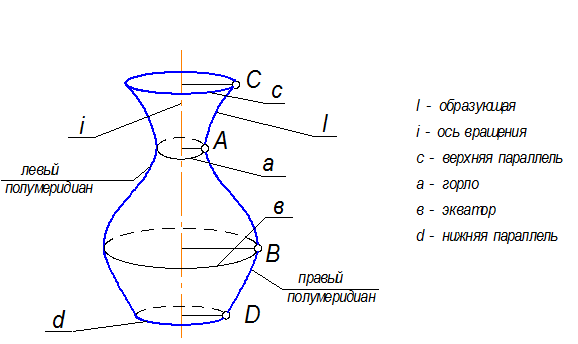
Рис. 2-76

При изображении поверхности вращения на комплексном чертеже обычно поверхность располагают так, чтобы ее ось была перпендикулярна к плоскости проекций. (например, i ^ П₁) Тогда все параллели проецируются на соответствующую плоскость (П₁) без искажения, причем экватор и горло на такой поверхности, как на рис. 2-76, определяют горизонтальную проекцию поверхности.

Меридиан, расположенный во фронтальной плоскости, проецируется без искажения на плоскость П₂. Этот меридиан называется фронтальным или главным, он определяет очерк проекции поверхности на фронтальную плоскость проекций и границу видимости относительно П₂.

Комплексный чертеж поверхности вращения общего вида

Задача: построить поверхность вращения общего вида, F(l, i) lã i, i ^ П₁ (рис. 2-77)

1. Задать проекции элементов определителя, графическая часть определителя может быть задана образующей (l) (рис. 2-77) или любой кривой (k), лежащей на поверхности и пересекающей все ее параллели.

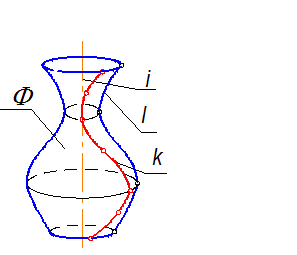
Рис. 2-77

Алгоритм построения

Если поверхность вращения F задана F(i, k), i ^ П_1, то:

1. Достраивается фронтальная проекция левого полумеридиана Проводятся проекции параллелей в виде отрезков прямых (тонкими линиями), перпендикулярных оси (i): горло, экватор, нижняя и верхняя; дополнительные параллели для точного

построения кривой (рис. 2.79).

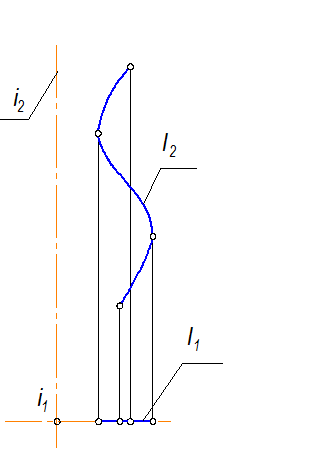
Рис. 2-78

Определитель задан осью – i и образующей – l, которая совпадает с плоскостью фронтального меридиана

2. После симметрично достроенного левого полумеридиана основной сплошной линией обводится очерк на П₂ -фронтальный (главный) меридиан.

3. Горизонтальная проекция поверхности вращения есть концентрично расположенные окружности-параллели, которые проецируются без искажения на П₁ (т.к. i ^ П₁) поэтому i₁- точка - центр окружностей. Экватор, верхняя параллель, горло на П₁ видимы, нижняя - невидима, т.к. расположена ниже экватора, а диаметр ее больше горла (рис.2-79).

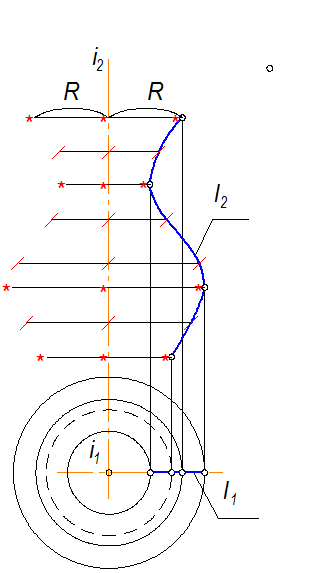
Рис. 2-79

4. Видимость точек, принадлежащих поверхности, относительно П₁ определяется особыми параллелями (заштрихованные зоны на фронтальной проекции поверхности): относительно П₂ - главным меридианом (заштрихованная зона на горизонтальной проекции). (Рис. 2-80)

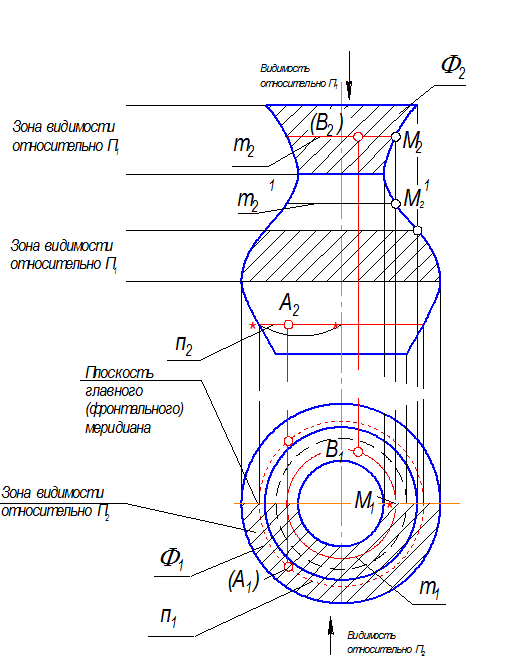
Рис. 2-80

5. Пусть А(А₂) и В(В₂) Î F , А₁ и В₂ = ? Чтобы построить вторую проекцию точки, лежащую на поверхности, через заданную проекцию точки проводят параллель.

а) Через точку А₂ проводят окружность - параллель (n₂). Замеряют радиус этой параллели от оси до очерка и строят ее горизонтальную проекцию (n₁). Из точки А₂ проводят линию связи на n₁ , которая пересекает n₁ в двух точках, выбирают нижнюю, т.к. А₂ видима, т.е. точка А₂ находится перед главным меридианом. Определяют видимость точки А₁ - она невидима, т.к. расположена ниже экватора (в незаштрихованной зоне).

б) Через точку В₁ проводят параллель m₁, отмечают точку пересечения с главным меридианом М₁, по принадлежности ему отмечают М₂, М₂¹, выбирают М₂, т.к. В₁ на П₁ видима, т.е. ее параллель на П₂ должна находиться в зоне видимости относительно П₁. Через М₂ проводят фронтальную проекцию этой параллели m₂, из точки В₁ проводят линию связи до пересечения с m₂.

Точка В₂ - невидима, т.к. на В₁ находится в незаштрихованной зоне, т.е. за главным меридианом.