Метод концентрических сфер

Для построения линии пересечения двух поверхностей вращения, оси которых пересекаются, иногда нецелесообразно использовать вспомогательные секущие плоскости, т.к. они могут не дать вспомогательных линий сечения, которые проецировались бы графически простыми линиями.

Прежде чем приступить к построению линии пересечения поверхностей вращения рассмотрим соосные поверхности.

Соосными называются поверхности, имеющие общую ось.

Две соосные поверхности пересекаются по окружностям, перпендикулярным общей оси.

Пример: соосные сфера и конус вращения пересекаются по линиям т и п. Точки А и В, вращаясь вокруг общей оси I, дадут окружности, принадлежащие конусу и сфере, которые и будут линиями их пересечения. Свойство сферы

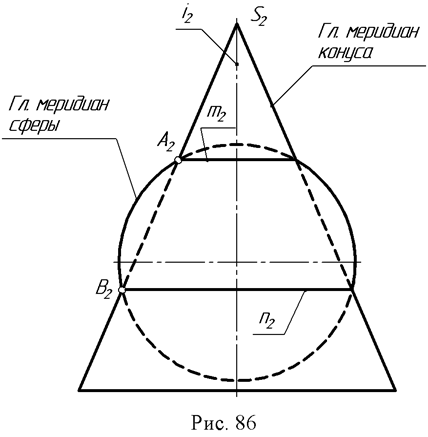
пересекать соосную с ней поверхность вращения по окружностям (параллелям поверхности) положено в основу способа применения сфер как посредников при нахождении линии пересечения поверхностей вращения. Для того чтобы вспомогательная секущая сфера пересекала по параллелям обе заданные поверхности, центр сферы должен лежать в точке пересечения осей заданных поверхностей. Если оси поверхностей вращения параллельны плоскости проекций, то параллели пересечения вспомогательной сферы с этими поверхностями проецируются на эту плоскость в прямые линии. Это - основа метода секущих концентрических сфер.

Пример: определить линию пересечения тора и конуса (рис. 87).

Заданы поверхности вращения, оси их пересекаются в точке О и по условию лежат в плоскости, параллельной фронтальной плоскости проекций.

Из точки О₂ проведем сферу произвольного радиуса R¹,, которая тор пересекает по линиям к₂ и l₂, конус по линиям т₂ и п₂ в пересечении которых определены точки А₂ и В₂, которые принадлежат фронтальной проекции линии пересечения тора и конуса.

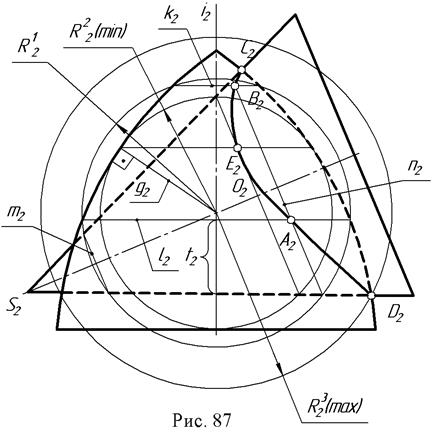
Изменяя радиус вспомогательных сфер, можно получить какое угодно число точек линии пересечения. Для определения максимального радиуса сферы, необходимо отметить точки пересечения очерковых линий, замерить расстояние от точки O₂ до этих точек и наибольшее из этих расстояний будет максимальным радиусом сферы (R³).

Для определения радиуса наименьшей сферы нужно из точки O₂ провести нормали к очерковым линиям каждой поверхности (g₂ и t₂). Больший из полученных отрезков и будет минимальным радиусом вспомогательной сферы (R²). При помощи этой сферы найдена точка Е₂. Именно с нее следует начинать искать точки линии пересечения поверхностей. Найденные точки соединяют плавной линией. Если нужно построить проекции этой линии на другие плоскости проекций, то это легко сделать, связав каждую точку пересечения с окружностью, лежащей на этой или другой поверхности вращения.

Вопросы для самопроверки.

1. Какие линии получаются при пересечении двух кривых оверхностей?

2. Назовите частные случаи пересечения поверхностей вращения второго порядка. Какой вид имеют линии пересечения в этих случаях?

3. Как пересекаются соосные поверхности вращения?

4. В каких случаях применяется метод соосных концентрических сфер? В чём он заключается?

Лекция 13. Развертки поверхностей.

Общие положения.

В инженерной практике развертывание поверхностей находит применение при разработке чертежей для раскроя плоского листового материала. Способы развертки поверхностей используются при проектировании тентовых сооружений, при строительстве резервуаров различной формы, воздуховодов и т.д. Обычно поверхность рассматривают как гибкую нерастяжимую оболочку. Развертыванием поверхности называется такое преобразование ее, в результате которого поверхность совмещается с плоскостью без складок и разрывов, а плоская фигура, полученная в результате этого преобразования, называется разверткой. В противном случае поверхность называется неразвертывающейся, и тогда для построения развертки ее разбивают на части, которые можно приближенно заменить развертывающимися поверхностями, а затем строить развертки этих частей.