Построение изображения в линзе

ПРЕДИСЛОВИЕ

Зрительная система человека функционирует так естественно, что трудно представить, что в основе зрительного акта лежат сложные процессы.

Прежде всего, глаз — это оптический прибор, который формирует изображение предметов внешнего мира на сетчатке глаза, где расположе- ны зрительные рецепторы — палочки и колбочки. Для понимания прин- ципов его работы необходимо знать некоторые элементы геометрической оптики, которые рассматриваются в первой главе учебно-методического пособия.

Во второй главе рассматривается строение глаза, особенности формирования изображений на сетчатке, вопросы аккомодации, остроты зрения, а также некоторые недостатки рефракции.

В третьей главе издания описано строение сетчатки, устройство зри- тельных рецепторов, а также биофизические механизмы преобразования светового раздражения в нервный импульс.

Окончательная обработка зрительного образа происходит в зритель- ных центрах головного мозга. Некоторые особенности цвето- и световос- приятия глаза рассмотрены в четвертой главе.

ЭЛЕМЕНТЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ

Оптика — это раздел физики, изучающий свойства и физическую природу света, а так же его взаимодействие с веществом. Видимый свет — это электромагнитное излучение в диапазоне длин волн от 400 до 760 нм. Уникальность этого диапазона заключается в том, что он является глав- ным источником информации для человека. К нему примыкают широкие области инфракрасного и ультрафиолетового излучения. Ультрафиоле- товое видимое и инфракрасное излучения образуют оптическую область спектра электромагнитного излучения. Она ограничена с одной стороны рентгеновскими лучами, а с другой — микроволновым диапазоном радиоизлучения. Под монохроматическим светом понимают электромаг- нитное излучение с очень узким диапазоном длин волн.

Раздел оптики, в котором законы распространения света рассматри- ваются на основе представлений о световых лучах, называется геометри-

ческой оптикой. Под световым лучом понимается направленная линия, вдоль которой распространяется световая энергия. Геометрическая оптика является приближенным методом построения изображений в оптических системах, но позволяет разобрать основные явления, связанные с прохож- дением через них света.

ЛИНЗА

Линзой называется прозрачное тело, ограниченное двумя сферически- ми (или плоской и сферической) поверхностями и по показателю прелом- ления отличающееся от окружающей среды. Линза называется тонкой, ес- ли ее толщина мала по сравнению с радиусами кривизны ее поверхностей.

Прямая О1О2, проходящая через центры кривизны поверхностей лин- зы, называется главной оптической осью (рис. 1.1). Для всякой линзы су- ществует точка О, называемая оптическим центром линзы. Любая прямая, проходящая через оптический центр, называется оптической осью линзы.

Лучи света, идущие вдоль оптических осей линзы, т. е. проходящие через ее центр, не преломляются.

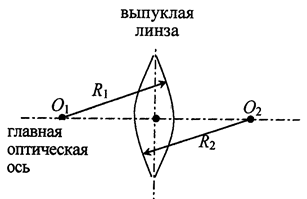
Рис. 1.1. Схематическое изображение линзы

Если луч света идет не вдоль оптической оси, то после прохождения линзы он изменяет свое направление, т. е. преломляется линзой.

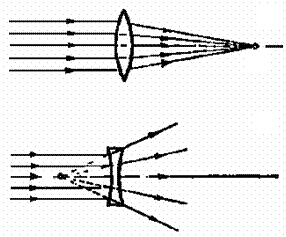
Если на линзу падает параллельный пучок света и после прохожде- ния линзы он сходится в одной точке F, то линзу называют собирающей (рис. 1.2, а), а точку F — действительным фокусом линзы. Если же параллельный пучок света после прохождения линзы расходится так, что кажется исходящим из одной точки, то линза называется рассеиваю- щей, а точка F — мнимым фокусом линзы (рис. 1.2, б).

а

F

б

F

Рис. 1.2. Линза: а — собирающая; б — рассеивающая

Если в фокус собирающей линзы поместить точечный источник све- та, то после прохождения линзы все лучи пойдут параллельно оптической оси линзы. Это свойство часто используется на практике для получения параллельных пучков света.

Фокус линзы, лежащий на главной оптической оси, называется глав- ным фокусом линзы, а все остальные ее фокусы (лежащие на других оптических осях) — побочными. Все фокусы линзы лежат в одной плос- кости, которая называется фокальной плоскостью линзы.

Расстояние F от центра линзы до ее главного фокуса называется

фокусным расстоянием и может быть определено по формуле:

1 =(n

æ1 1 ö

-1) ç - ÷,

(1.1)

F èR1

nл

R2 ø

где

n21 = -— относительный показатель преломления линзы и окру-

n1

жающей среды; R1 и R2 — радиусы кривизны ее 1-й и 2-й (по ходу луча) поверхностей, которые считаются положительными, если их центры расположены справа (т. е. по ходу луча) от линзы, и отрицательными, если слева от нее.

Если F > 0, то фокус действительный и линза собирающая, а если

F < 0, то фокус мнимый и линза рассеивающая.

Отметим, что каждая линза имеет передний и задний (по ходу луча) фокусы. Если по обе стороны линзы одинаковая среда, то переднее и зад- нее фокусные расстояния линзы равны. Если же по обе стороны линзы разные среды (например, по разные стороны роговицы глáза находятся воздух и водянистая влага) с показателями преломления n1 и n2, то перед- нее F1 и заднее F2 фокусные расстояния будут отличаться примерно в (n1/n2) раз.

ОПТИЧЕСКАЯ СИЛА ЛИНЗЫ

Основной характеристикой и мерой преломляющего действия линзы служит ее оптическая сила — величина, обратная фокусному расстоянию линзы.

D=1

F

. (1.2)

В СИ оптическая сила линзы измеряется в диоптриях (дптр), при этом фокусное расстояние должно измеряться в метрах:

1 дптр = 1 м–1.

Оптической силой в одну диоптрию обладает линза с фокусным расстоянием 1 м. У собирающих линз оптическая сила положительна, у рассеивающих — отрицательна. Оптическая сила зависит от показате-

лей преломления вещества линзы и среды, окружающей линзу, а также от радиусов кривизны ее поверхностей (см. формулу (1.1)).

ПОСТРОЕНИЕ ИЗОБРАЖЕНИЯ В ЛИНЗЕ

Чтобы получить изображение точки, создаваемое линзой, необходи- мо найти пересечение лучей, исходящих из этой точки, после их прелом- ления в линзе. Для этого удобно использовать любую пару из следующих трех лучей (рис. 1.3):

а) луч, параллельный оптической оси, после преломления в линзе проходит через ее задний фокус;

б) луч, проходящий через передний главный фокус, после преломле- ния идет параллельно главной оптической оси;

в) луч, идущий через оптический центр линзы, не преломляется, т. е. после преломления идет в том же направлении.

линза

A

F

B1

B O

D f

A1

Рис. 1.3. Построение изображения в линзе

Пересечение этих двух лучей, исходящих из точки А, даст точку А1, являющуюся изображением точки А. Опуская из точки А1 перпендикуляр на главную оптическую ось, найдем точку В1 — изображение точки В. Построения этих лучей выполняются без затруднений.

Если лучи, исходящие из точки А, пересекаются после прохождения линзы в точке А1, то изображение называется действительным.Его можно наблюдать и зарегистрировать, поместив в плоскости пересечения лучей экран или фотопленку. Если же лучи, исходящие из точки А, после прохождения линзы расходятся, а их продолжения пересекаются в точке А1, то такое изображение называется мнимым — оно всегда прямое и рас- положено по ту же сторону линзы, что и предмет. Такое изображение нельзя наблюдать непосредственно на экране или зафиксировать на фото- пленке, но можно увидеть глазом (лупа, микроскоп).

ФОРМУЛА ЛИНЗЫ

Если предмет находится на расстоянии d, а его изображение на рас- стоянии f от линзы с фокусным расстоянием F, то выполняется соотноше- ние, называемое формулой линзы:

1 +1

d f

=1 .

F

(1.3)

Здесь фокусное расстояние F считается положительным для соби- рающих линз и отрицательным — для рассеивающих. Расстояние d от предмета до линзы всегда положительно, а расстояние f от линзы до изображения положительно для действительных изображений и отри- цательно для мнимых.

Если предмет находится на бесконечности (т. е. удален на большое расстояние d → ∞), то его изображение будет расположено в фокусе линзы (f = F), а по мере приближения предмета к линзе его изображение удаляется от линзы и f > F. Отношение линейных размеров H изображе- ния к линейным размерам h предмета называется линейным увеличением Г и может быть выражено соотношением:

Г = H= fh d

= F

d-F

, (1.4)

где H — размер изображения, h — размер предмета.

Для рассеивающей линзы расстояние f всегда отрицательное, т. е. она дает только мнимые прямые уменьшенные изображения

( 1 =-1

f F

-1 <0,

d

F

Г =

d + F

< 1 ).

Собирающая линза может давать как действительные, так и мнимые изображения.

Действительные изображения предмета формируются в тех случаях, когда он расположен перед передним фокусом линзы, т. е. при d > F. При этом можно получить три вида действительных изображений:

уменьшенное (если d > 2F), равное (d = 2F) и увеличенное (F < d < 2F). Действительные изображениявсегда находятся по другую сторону линзы относительно предмета и всегда перевернутые.

Собирающая линза дает мнимое увеличенное изображение, если предмет расположен между передним фокусом и линзой, при d < F. Напомним, что мнимое изображение всегда прямоеи находится по ту же сторону от линзы, что и предмет.

АБЕРРАЦИИ ЛИНЗЫ

Под аберрацией понимают погрешности изображения в реальной оп- тической системе, вызванные отклонением хода световых лучей по срав- нению с идеально центрированной оптической системой.

Сферическая аберрация возникает в силу того, что края линзы, огра- ниченной сферическими поверхностями, преломляют параллельные монохроматические лучи сильнее, чем центральная ее часть (рис. 1.4). В результате фокус имеет вид не точки, а небольшого кружка (кружок рассеяния). Сферическая аберрация сказывается тем сильнее, чем больше кривизна поверхностей, ограничивающих линзу и чем шире падающий на нее световой пучок.

Рис. 1.4. Сферическая аберрация

Хроматическая аберрация обусловлена тем, что показатель прелом- ления вещества линзы зависит от длины волны. Это означает, что красные и фиолетовые лучи преломляются линзой неодинаково (фиолетовые всегда сильнее красных), и фокусы для них не совпадают (рис. 1.5). В результате, при падении на линзу белого света вместо точки получится окрашенное пятно.

Рис. 1.5. Хроматическая аберрация

Астигматизм линзы обусловлен отклонением ее формы от правиль- ной сферической. В результате проходящие через нее световые лучи не могут после своего преломления собраться в одну фокальную точку. Они образуют две фокальные линии — переднюю (А1A2) и заднюю (B1B2), — расположенные на разных расстояниях от линзы (рис. 1.6). Такая система не может дать одновременно четкое изображение, например, горизон- тальных и вертикальных линий.

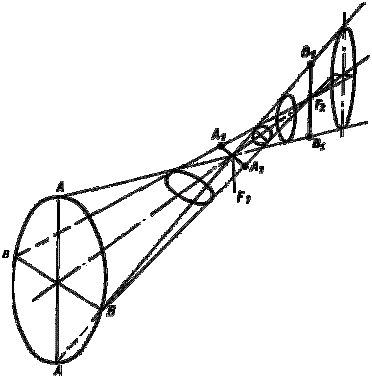
Рис. 1.6. Астигматизм

ЛУПА

Лупой называется собирающая линза с фокусным расстоянием, как правило, не менее 0,1 м, используемая для получения увеличенных мнимых изображений предмета.

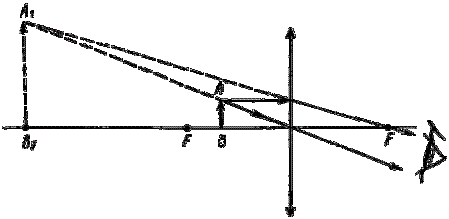
Лупа помещается перед глазом, а рассматриваемый предмет — обыч- но на расстоянии, немного меньшем фокусного (d < F), т. к. чем меньше (F – d), тем больше увеличение (см. формулу 1.4). Мнимое прямое увели- ченное изображение, как правило, располагается на расстоянии наилуч- шего зрения f = d = 0,25 м (рис. 1.7). Лупа позволяет «приблизить» пред- мет к глазу, и предмет оказывается виден под большим углом.

Рис. 1.7. Изображение, полученное при помощи лупы

Увеличение лупы определяется по формуле:

D

Г = , (1.5)

F

где D — расстояние наилучшего зрения; F — фокусное расстояние лупы.

Чем короче фокусное расстояние линзы, тем больше ее увеличение, но при этом возрастают искажения (аберрации) изображений. Увеличение лупы обычно лежит в пределах от 2 до 20. Наиболее распространены лупы с 4 ÷ 10-кратным увеличением.