Способ перемены плоскостей проекций
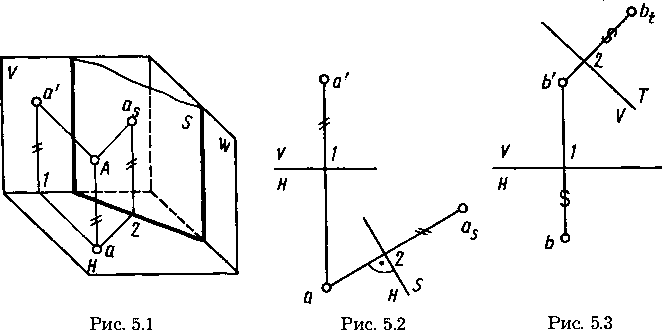 Этот способ широко применяют в машиностроении и приборостроении. Сущность способа перемены плоскостей проекций заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система V, Н дополняется плоскостями, образующими с V, или Н, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.
Этот способ широко применяют в машиностроении и приборостроении. Сущность способа перемены плоскостей проекций заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система V, Н дополняется плоскостями, образующими с V, или Н, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.
Каждая новая система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение, наиболее удобное для выполнения требуемого построения.
На рисунке 5.1 показано преобразование проекций точки А из системы V, Н в систему S, Н, в которой вместо плоскости V введена новая плоскость S, а плоскость Н осталась неизменной. При этом S перпендикулярна Н. В системе S, Н горизонтальная проекция а точки А осталась неизменной. Проекция as точки А на плоскости S находится от плоскости Н на том же расстоянии, что и проекция a' точки А на плоскости V. Это условие позволяет легко строить проекцию точки на чертеже (рис. 5.2) на новой плоскости проекций. Для этого в новой системе (Н, S) из проекции точки (а) на сохраняющейся плоскости проекций проводят линию связи, перпендикулярную к новой оси проекций (S/H). На этой линии связи отмечают расстояние от оси до проекции as точки на новой плоскости проекций S, равное расстоянию от преобразуемой проекции точки а' до оси проекций V/H в системе V, Н (| аs—2| = | а'—1|).
При введении новой плоскости проекций, перпендикулярной фронтальной плоскости проекций (например, плоскости Т на рис. 5.3), расстояние от проекции (bt) до новой оси проекций равно расстоянию от горизонтальной проекции (b) до оси V/H (|b-1| = |bt-2|).
В дальнейшем, при введении новой плоскости проекций, ось проекций можно обозначать в виде дроби, черта которой лежит на оси; каждую букву при этом пишут как бы на «своей» плоскости.
 Проекции точек на новых плоскостях проекций удобно отмечать индексами плоскости (например,а, bt, и т. п.).
Проекции точек на новых плоскостях проекций удобно отмечать индексами плоскости (например,а, bt, и т. п.).
Перемену плоскостей проекций можно производить последовательно несколько раз.
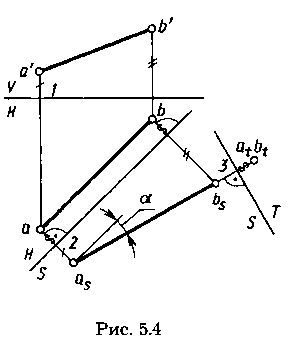
Четыре основные задачи преобразования. Определение величины отрезка АВ общего положения показано на рисунке 5.4. Для этого плоскость V заменена на новую плоскость проекций S, параллельную отрезку (ось S/H параллельна оси ab). Расстояния от оси S/H до at и bt соответственно равны расстояниям от а' и b' до оси V/H соответственно (|аt—2|—|а'—1|).Одновременно с определением натуральной величины отрезка определена величина а угла наклона отрезка АВ к плоскости Н.
Приведение отрезка прямой общего положения в проецирующее положение. На рисунке 5.4 новая система плоскостей проекций H/S относительно отрезка АВ находится в частном положении (пл. S || АВ). Введем еще одну новую плоскость проекций Т, перпендикулярную плоскости проекций S и отрезку АВ (ось проекций T/S перпендикулярна проекции asьs). Относительно этой плоскости проекций Т отрезок АВ занимает проецирующее положение (проекции аt и bt совпадают, | а—2| = | аt—3|).
Для преобразования проекций отрезка общего положения на чертеже в проецирующее положение требуется введение двух новых плоскостей проекций последовательно: первой — параллельно отрезку, второй — перпендикулярно ему с условием перпендикулярности между исходными и новыми плоскостями проекций.
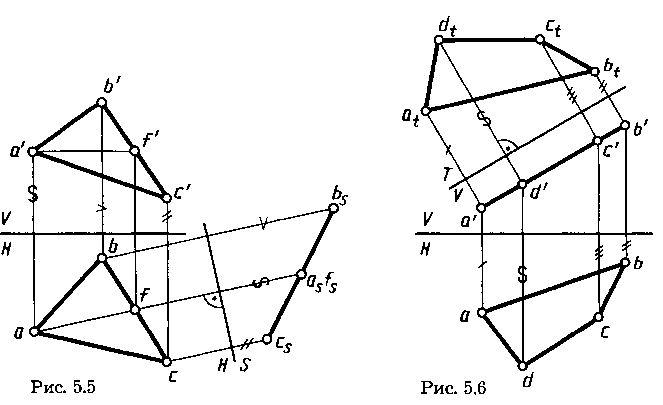
Приведение плоской фигуры общего положения в проецирующее положение. Решение основывается на предыдущей задаче. Построение выполняют с помощью одной из линий частного положения, например горизонтали с проекциями a'f', af (рис. 5.5). Новая плоскость проекций S в этом случае выбрана перпендикулярно горизонтали AF (ось перпендикулярна проекции af) и соответственно перпендикулярно плоскости Н.
Определение натурального вида плоской фигуры, расположенной в проецирующем положении(рис. 5.6). Построение выполнено путем введения новой плоскости проекций Т,перпендикулярной плоскости V и параллельной плоскости четырехугольника с проекциямиa'b'c'd' и а, b, с, d (ось T/V параллельна проекции a'b'c'd'). Проекция atbtctdt является натуральным видом заданного четырехугольника.
 Следовательно, последовательным введением двух новых плоскостей проекций могут быть определены: натуральный вид плоской фигуры, принадлежащей плоскости общего положения, и углы наклона плоскости к плоскостям проекций.
Следовательно, последовательным введением двух новых плоскостей проекций могут быть определены: натуральный вид плоской фигуры, принадлежащей плоскости общего положения, и углы наклона плоскости к плоскостям проекций.
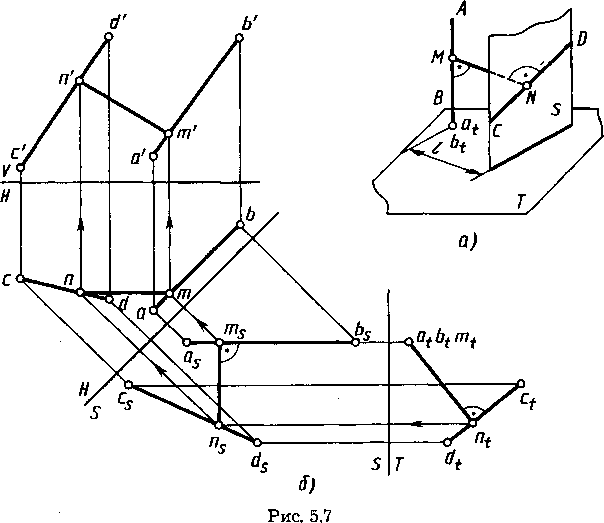 Определение расстояния между двумя скрещивающимися прямыми. Это расстояние выражается величиной общего перпендикуляра MN к заданным прямым АВ и CD (рис. 5.7, а). Для определения его длины удобно, чтобы одна из прямых располагалась перпендикулярно плоскости проекций. Выше было показано, что для этого надо последовательно ввести две новые плоскости проекций (рис. 5.7, б), например:
Определение расстояния между двумя скрещивающимися прямыми. Это расстояние выражается величиной общего перпендикуляра MN к заданным прямым АВ и CD (рис. 5.7, а). Для определения его длины удобно, чтобы одна из прямых располагалась перпендикулярно плоскости проекций. Выше было показано, что для этого надо последовательно ввести две новые плоскости проекций (рис. 5.7, б), например:
На плоскость Т прямая АВ проецируется в точку at=bt. Проведя перпендикуляр из точки аt=bt, на проекцию ctdt находим проекцию п, точки N пересечения его с прямой CD. Отметим
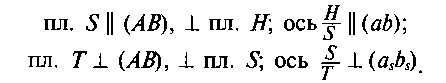
проекцию т, точки М, совпадающую с проекциями точек аtbt. Искомое расстояние определено —mtnt. На чертеже стрелками указано построение проекций тп и т'п' общего перпендикуляра к двум скрещивающимся прямым в системе V, Н.
