Принадлежность точки или линии поверхности

Для любой поверхности, если она задана, можно решить задачу на принадлежность точки или линии данной поверхности.

Точка принадлежит поверхности, если она лежит на линии, принадлежащей данной поверхности (рис. 70 а, б). Для построения недостающей проекции точки на поверхности вращения через эту точку проводят параллель, для линейчатой поверхности – прямолинейную образующую.

Например:

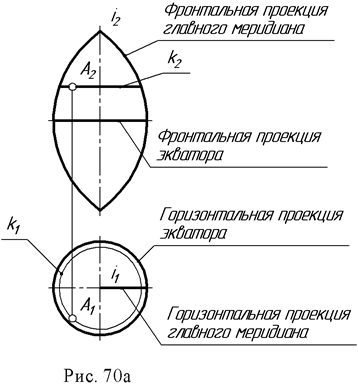
1. На поверхности тора определить горизонтальную проекцию точки А по заданной ее фронтальной проекции. Через точку А₂ проведена параллель k и на ней, используя линию проекционной связи, найдена точка А₁. На этом чертеже показана плоскость главного меридиана. Это - сечение поверхности плоскостью α ||П₂, проходящей через ось тора.

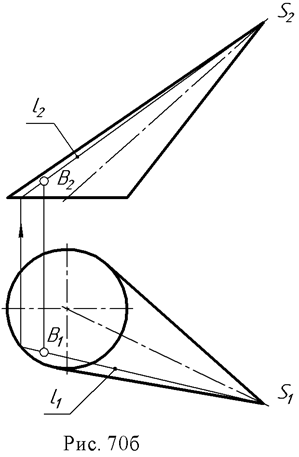
2. На поверхности конуса определить фронтальную проекцию точки В по заданной горизонтальной (рис. 70б).

Через горизонтальную проекцию В₁ проведена проекция образующей l₁, построена фронтальная проекция образующей l₂, и на ней лежит недостающая фронтальная проекция В₂ точки В.

Вопросы для самопроверки

1.Какие кривые поверхности называют поверхностями Каталана?

2.Какую поверхность называют цилиндроидом? Коноидом? Гипаром?

3.Как образуются поверхности вращения?

4.Укажите основные элементы поверхностей вращения.

5.Назовите поверхности вращения с прямолинейной образующей.

6.Назовите наиболее распространенные поверхности вращения с криволинейной образующей.

7.Как построить точку и линию, принадлежащие поверхности?

Лекция 9. Пересечение поверхности плоскостью.

Общие положення

В результате пересечения кривой поверхности плоскостью в общем случае может получиться плоская кривая линия, характер которой зависит от вида поверхности и от положения плоскости. Полученная кривая линия складывается из точек, одновременно принадлежащих плоскости и поверхности.

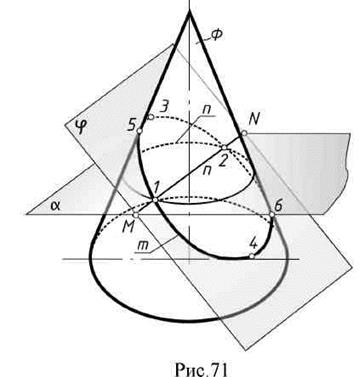
Пусть задана поверхность произвольного вида Ф и плоскость φ (рис.71).

Алгоритм решения.

1. Поверхность и плоскость пересекают вспомогательной плоскостью посредником α.

2.Находят линию пересечения плоскости - посредника α с поверхностью Ф:

n = Ф ∩ α

3. Находят линию пересечения плоскости - посредника с заданной плоскостью φ: MN= φ ∩ α.

4. Отмечают точки, в которых эти линии пересекутся: 1, 2 = (MN ∩ n).

Точки 1 и 2, являясь общими для данных поверхности и плоскости, будут точками искомой линии пересечения.

5. Для построения линии пересечения необходимо найти еще ряд точек (3, 4, 5 …), используя плоскости - посредники.

6. Найденные точки плавно соединить, получается линия - m = φ ∩ Ф линия пересечения поверхности плоскостью; если поверхность замкнутая, то эта линия называется сечением. При выборе вспомогательных секущих плоскостей - посредников следует руководствоваться простотой построения линии пересечения этих плоскостей с заданной поверхностью. Эти линии должны быть графически простыми; для поверхностей вращения – окружности; для линейчатых поверхностей – прямолинейные образующие.