Логарифмическая функция
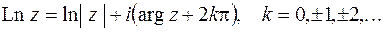 (3.9)
(3.9)
Из (3.9) видно, что логарифмическая функция – функция многозначная, ее значения для данного значения z отличаются друг от друга на число 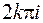 . Значение логарифма, соответствующее
. Значение логарифма, соответствующее 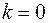 , называется главным и обозначается
, называется главным и обозначается
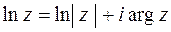 (3.10)
(3.10)
Логарифмическая функция комплексного переменного обладает известными свойствами логарифма действительного переменного.
6. Обобщенные степенная и показательная функции
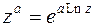 , (3.11)
, (3.11)
где a – любое комплексное число;
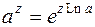 , (3.12)
, (3.12)
где 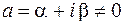 .
.
В силу многозначности логарифма, выражение, определяемое равенством (3.12), многозначно. Его главным значением называется то, которое получается при подстановке в правую часть (3.12) 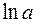 вместо Ln a.
вместо Ln a.
УПРАЖНЕНИЯ
41. Выделить действительную и мнимую части функции 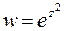 .
.
Решение. Пусть 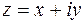 . Тогда по определению показательной функции (3.2) имеем
. Тогда по определению показательной функции (3.2) имеем 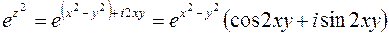 , откуда
, откуда 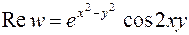 ,
, 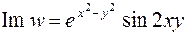 .
.
42. Найти значение функции 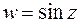 в точке
в точке 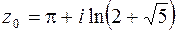 , иначе говоря, найти образ точки
, иначе говоря, найти образ точки 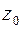 при отображении
при отображении 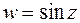 .
.
Решение. Используя формулы привидения и (3.8), находим 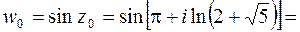
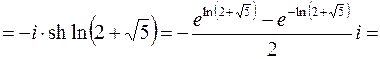
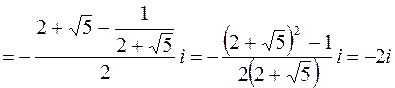 ,
, 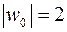 .
.
Этот пример показывает, что функция 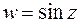 в комплексной области может принимать значения, больше единицы по модулю.
в комплексной области может принимать значения, больше единицы по модулю.
43. Найти корни уравнения 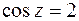 и изобразить их на плоскости.
и изобразить их на плоскости.
Решение. По определению функции 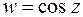 , из (3.4) имеем
, из (3.4) имеем
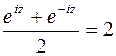 , откуда
, откуда 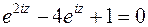 . Полученное квадратное уравнение относительно
. Полученное квадратное уравнение относительно 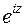 имеет корни
имеет корни 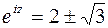 . Следовательно, в силу определения логарифмической функции (3.9) с учетом (3.10) получаем
. Следовательно, в силу определения логарифмической функции (3.9) с учетом (3.10) получаем
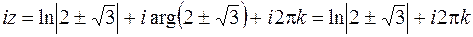 ,
, 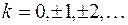 . Отсюда определяем
. Отсюда определяем 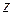 :
: 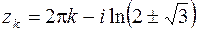 ,
, 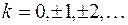 .
.
Итак, получены две серии корней
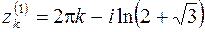 ,
, 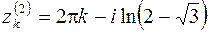 , (
, ( 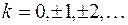 ). Учитывая, что
). Учитывая, что 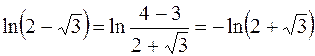 , вторая серия корней
, вторая серия корней 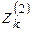 перепишется в виде
перепишется в виде 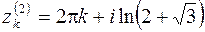 .
.
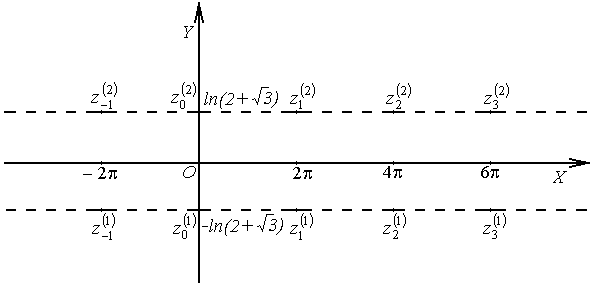 Рис.3.2 Рис.3.2 |
Таким образом, корнями данного уравнения являются точки, расположенные на прямых, параллельных действительной оси 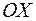 и отстоящих от нее на расстоянии
и отстоящих от нее на расстоянии 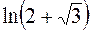 (рис. 3.2).
(рис. 3.2).
При изображении чисел учтено, что 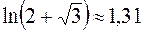 .
.
44. При отображении 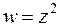 найти:
найти:
а) образ прямой линии 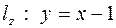 ;
;
б) образы прямоугольной сетки, т.е. прямых, параллельных осям координат: 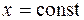 ,
, 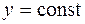 ;
;
в) образ линии 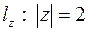 ,
, 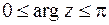 ;
;
г) образ области 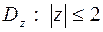 ,
, 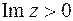 ,
, 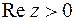 ;
;
д) образ области 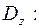 внутренность треугольника с вершинами в точках 0; 1;
внутренность треугольника с вершинами в точках 0; 1; 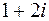 .
.
Решение. а) Линия 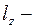 прямая, заданная уравнением в действительных переменных, от которого можно перейти к параметрическим уравнениям
прямая, заданная уравнением в действительных переменных, от которого можно перейти к параметрическим уравнениям 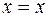 ,
, 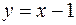 .
.
Полагая 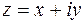 , определим действительную и мнимую части функции
, определим действительную и мнимую части функции 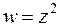 :
: 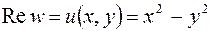 ,
, 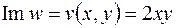 .
.
Для того, чтобы найти уравнение образа 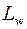 данной прямой
данной прямой 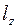 , исключим
, исключим 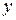 из уравнений
из уравнений 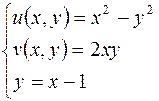 , в результате чего получим параметрические уравнения
, в результате чего получим параметрические уравнения 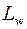 :
: 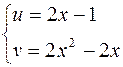 . Если из полученных уравнений
. Если из полученных уравнений 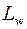 исключить параметр
исключить параметр 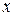 , то придем к уравнению образа в плоскости
, то придем к уравнению образа в плоскости 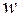 в действительных переменных
в действительных переменных 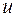 и
и 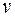 :
: 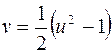 . Как видно, искомый образ есть парабола (рис. 3.3);
. Как видно, искомый образ есть парабола (рис. 3.3);
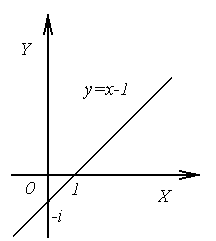 | 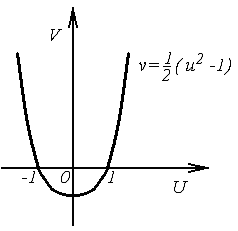 |
Рис.3.3
б) Чтобы найти образы семейства прямых 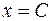 , подставим вместо
, подставим вместо 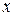 его значение в действительную и мнимую части функции
его значение в действительную и мнимую части функции 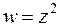 :
: 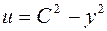 ,
, 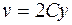 . Исключив отсюда
. Исключив отсюда 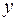 , получим
, получим 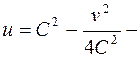 семейство парабол, симметричных относительно оси
семейство парабол, симметричных относительно оси 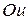 , вершины которых находятся на положительной части этой оси, а ветви направлены в сторону отрицательной части оси
, вершины которых находятся на положительной части этой оси, а ветви направлены в сторону отрицательной части оси 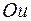 (рис. 3.4). В частности, при
(рис. 3.4). В частности, при 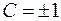 и
и 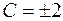 соответственно имеем
соответственно имеем 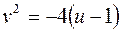 и
и 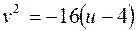 .
.
Мнимая ось 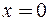 плоскости
плоскости  отобразится в линию
отобразится в линию 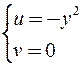 .
.
Второе из равенств указывает, что образ прямой 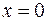 на оси
на оси 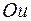 , а из первого равенства следует, что
, а из первого равенства следует, что 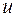 может принимать лишь отрицательные значения. Следовательно, мнимая ось
может принимать лишь отрицательные значения. Следовательно, мнимая ось 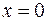 плоскости
плоскости  отображается на отрицательную часть действительной оси плоскости
отображается на отрицательную часть действительной оси плоскости 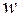 :
: 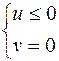 . Семейство прямых
. Семейство прямых 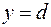 отображается в семействе кривых
отображается в семействе кривых 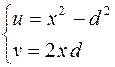 или
или 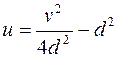 .
.
Рис.3.4 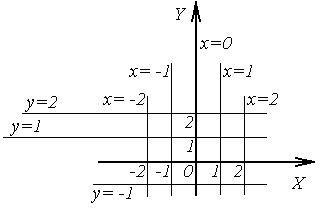 | 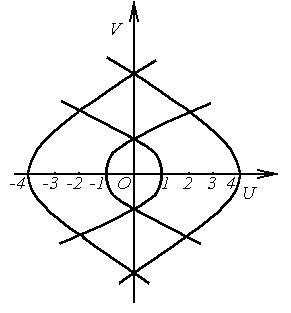 |
Получим семейство парабол симметричных относительно оси 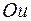 . Вершины находятся на отрицательной части
. Вершины находятся на отрицательной части 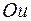 , направление ветвей совпадает с положительным направлением оси
, направление ветвей совпадает с положительным направлением оси 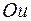 (рис.3.4). В частности, при
(рис.3.4). В частности, при 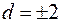 имеем
имеем 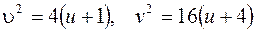 .
.
При 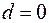 получаем
получаем 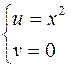 . Это значит, что действительная ось
. Это значит, что действительная ось 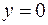 плоскости
плоскости 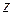 отображается в положительную часть действительной оси плоскости
отображается в положительную часть действительной оси плоскости 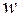 :
: 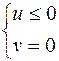 .
.
Итак, сетка прямых  линий, отразится в «сетку» параболических кривых в плоскости
линий, отразится в «сетку» параболических кривых в плоскости  .
.
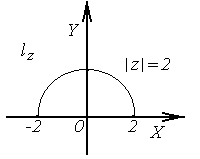 | 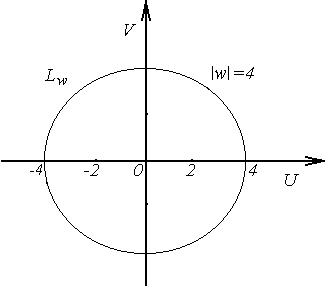 |
Рис.3.5
в) Линия 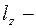 полуокружность верхней полуплоскости с центром в начале координат и радиусом
полуокружность верхней полуплоскости с центром в начале координат и радиусом 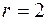 . Уравнение кривой запишем в комплексно–параметрической форме
. Уравнение кривой запишем в комплексно–параметрической форме 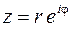 , где
, где 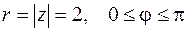 .
.
Тогда 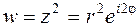 , откуда следует, что
, откуда следует, что 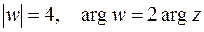 . Значит, при отображении
. Значит, при отображении 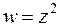 точки, лежащие на полуокружности плоскости z, перейдут в точки, лежащие на окружности
точки, лежащие на полуокружности плоскости z, перейдут в точки, лежащие на окружности 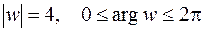 плоскости
плоскости 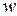 (рис.3.5).
(рис.3.5).
г) Для отыскания образа 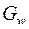 области
области 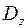 можно найти образ
можно найти образ 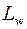 ее границы (если область замкнутая или ограниченная), а затем выяснить расположение искомой области относительно ее границы. Ели произвольная точка
ее границы (если область замкнутая или ограниченная), а затем выяснить расположение искомой области относительно ее границы. Ели произвольная точка 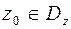 переходит в точку
переходит в точку 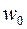 , лежащую внутри контура
, лежащую внутри контура 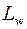 , то область
, то область 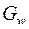 есть ограниченная область – множество точек плоскости
есть ограниченная область – множество точек плоскости 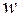 , лежащих внутри контура. Если точка
, лежащих внутри контура. Если точка 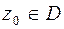 переходит в точку
переходит в точку 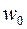 , лежащую вне контура, то область
, лежащую вне контура, то область 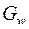 есть область неограниченная, расположенная вне линии
есть область неограниченная, расположенная вне линии 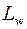 . По условию область
. По условию область 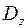 плоскости
плоскости  есть четверть круга в первой четверти координатной плоскости (рис.3.6).
есть четверть круга в первой четверти координатной плоскости (рис.3.6).
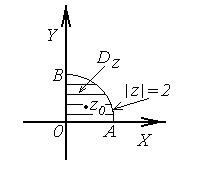 | 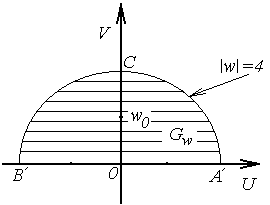 |
Рис.3.6
Как было показано в предыдущих пунктах б) и в) задачи, мнимая ось 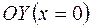 переходит в отрицательную полуось
переходит в отрицательную полуось 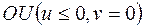 , действительная ось
, действительная ось 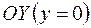 – в положительную полуось
– в положительную полуось 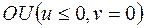 , а дуга
, а дуга 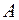 окружности плоскости z переходит в полуокружность
окружности плоскости z переходит в полуокружность 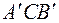 верхней полуплоскости
верхней полуплоскости 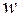 .
.
На основании этого можно заключить, что образом контура 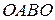 плоскости
плоскости  является контур
является контур 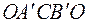 плоскости
плоскости 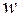 (рис.3.6). Чтобы убедиться в этом, четверть круга
(рис.3.6). Чтобы убедиться в этом, четверть круга 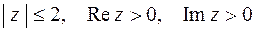 отображается в верхний полукруг:
отображается в верхний полукруг: 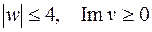 , покажем, что произвольная точка области
, покажем, что произвольная точка области 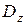 переходит в точку полукруга
переходит в точку полукруга 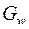 . Например, при
. Например, при 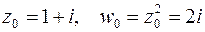 , т.е.
, т.е. 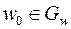 .
.
д) область 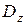 изображена на рис 3.7,а. Найдем последовательно образы участков границы области
изображена на рис 3.7,а. Найдем последовательно образы участков границы области 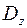 , при условии, что
, при условии, что 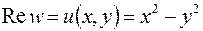 ,
, 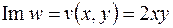 .
.
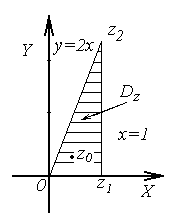 a) a) | 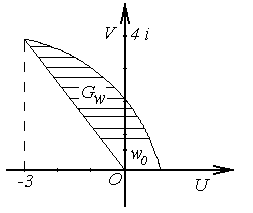 б) б) |
Рис.3.7
Отрезок 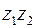 , уравнение которого
, уравнение которого 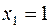 , причем
, причем 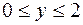 , имеет своим образом линию:
, имеет своим образом линию: 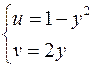 . Легко установить, что это есть часть параболы
. Легко установить, что это есть часть параболы 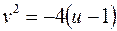 , т.к.
, т.к. 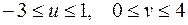 (рис.3.7, б).
(рис.3.7, б).
Отрезок 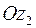 , уравнение которого
, уравнение которого 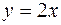 , где
, где 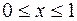 , имеет своим образом линию:
, имеет своим образом линию: 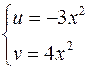 , откуда имеем
, откуда имеем 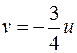 , причем
, причем 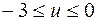 ,
, 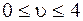 (рис.3.7, б).
(рис.3.7, б).
Отрезок 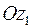 :
: 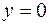 ,
, 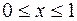 отображается в отрезок оси
отображается в отрезок оси 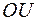 , так как
, так как 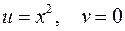 и
и 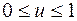 (рис.3.7, б).
(рис.3.7, б).
Чтобы показать, откуда переходит внутренность треугольника 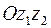 , возьмем точку
, возьмем точку 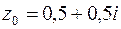 .
.
Найдем соответствующие значения 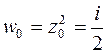 . Таким образом, отображением прямолинейного треугольника плоскости
. Таким образом, отображением прямолинейного треугольника плоскости  , осуществляемого функцией
, осуществляемого функцией 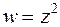 , является криволинейный треугольник плоскости
, является криволинейный треугольник плоскости 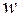 , представленный на рис.3.7, б.
, представленный на рис.3.7, б.
45. Отобразить с помощью функции 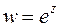 декартову координатную сетку.
декартову координатную сетку.
Решение. Введем на плоскости  декартовы, а на плоскости
декартовы, а на плоскости 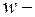 полярные координаты, т.е. положим
полярные координаты, т.е. положим 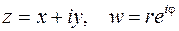 . По определению показательной функции имеем
. По определению показательной функции имеем 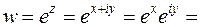 (по формуле Эйлера)
(по формуле Эйлера) 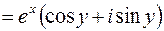 . Следовательно,
. Следовательно,
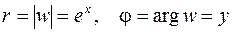 . (3.13)
. (3.13)
Найдем образы координатных линий 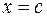 . Из равенства (3.13) имеем
. Из равенства (3.13) имеем
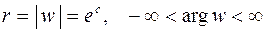 . (3.14)
. (3.14)
Когда точка  пробегает прямую
пробегает прямую 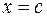 , ее образ, как следует из системы (3.14), пробегает окружность, причем бесконечно много раз. В силу периодичности показательной функции
, ее образ, как следует из системы (3.14), пробегает окружность, причем бесконечно много раз. В силу периодичности показательной функции 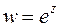 рассмотрим изменение ее аргумента в промежутке
рассмотрим изменение ее аргумента в промежутке 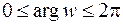 , что соответствует изменению
, что соответствует изменению 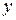 в том же интервале. Тогда образами отрезков
в том же интервале. Тогда образами отрезков 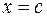 ,
, 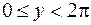 являются окружности радиуса
являются окружности радиуса 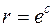 с центром в начале координат, пробегаемые один раз (рис.3.8).
с центром в начале координат, пробегаемые один раз (рис.3.8).
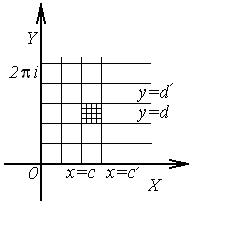 | 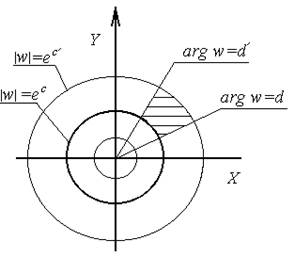 |
Рис.3.8
Найдем теперь образы координатных прямых 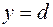 ,
, 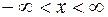 и пусть
и пусть 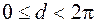 . В силу равенства (3.13) имеем
. В силу равенства (3.13) имеем
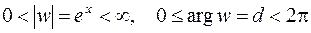 . (3.15)
. (3.15)
Из системы (3.15) следует: когда точка  пробегает прямую
пробегает прямую 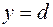 , точка
, точка 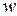 пробегает луч
пробегает луч 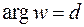 , исходящий из начала координат
, исходящий из начала координат 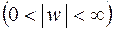 (рис.3.8).
(рис.3.8).
Итак, функция 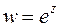 отображает прямые, параллельные мнимой оси
отображает прямые, параллельные мнимой оси 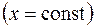 , в окружности с центром в начале координат, а прямые, параллельные действительной оси
, в окружности с центром в начале координат, а прямые, параллельные действительной оси 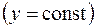 , в лучи, выходящие из начала координат, иначе говоря, декартова прямоугольная сетка отображается в полярную координатную сетку. При этом заштрихованный прямоугольник
, в лучи, выходящие из начала координат, иначе говоря, декартова прямоугольная сетка отображается в полярную координатную сетку. При этом заштрихованный прямоугольник 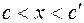 ,
, 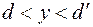 (
( 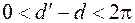 ) плоскости
) плоскости  отображается в заштрихованную часть кольца плоскости
отображается в заштрихованную часть кольца плоскости 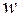 (рис. 3.8).
(рис. 3.8).
46. Показать, что 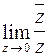 не существует.
не существует.
Решение. Пусть точка  стремится к нулевой точке по оси
стремится к нулевой точке по оси 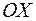 .
.
Тогда 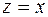 и
и 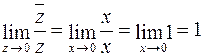 . Пусть теперь
. Пусть теперь 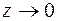 по оси
по оси 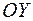 .
.
Тогда 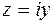 ,
, 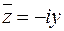 и
и 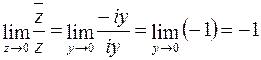 . Таким образом, пределы по двум направлениям различны, и, следовательно,
. Таким образом, пределы по двум направлениям различны, и, следовательно, 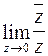 не существует.
не существует.
47. Вычислить 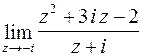 .
.
Решение. 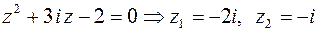 .
.
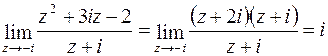 .
.
