Начертательная геометрия

1. Центральные проекции и их основные свойства.

При центральном проецировании (построении центральных проекций) задают плоскость проекций и центр проекций — точку, не лежащую в плоскости проекций. На рисунке 1.1 плоскость Р — плоскость проекций, точка S — центр проекций.

Для проецирования произвольной точки через нее и центр проекций проводят прямую. Точка пересечения этой прямой с плоскостью проекций и является центральной проекцией заданной точки на выбранной плоскости проекций.

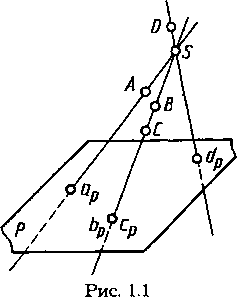
На рисунке 1.1 центральной проекцией точки А является точка ар пересечения прямой SA с плоскостьюР. Так же построены центральные проекции bр, ср, dpточек В, С, D на плоскости Р.

Прямые, проходящие через центр проекций и проецируемые точки, называют проецирующими прямыми.

Центральные проекции bр и ср двух различных точек В и С в пространстве, которые располагаются на одной проецирующей прямой, совпадают. Все множество точек пространства, принадлежащих одной проецирующей прямой, имеет при одном центре проецирования одну центральную проекцию на заданной плоскости проекций.

Следовательно, при заданных плоскости проекций и центре проецирования одна точка в пространстве имеет одну центральную проекцию. Но одна центральная проекция точки не позволяет однозначно определить положение точки в пространстве.

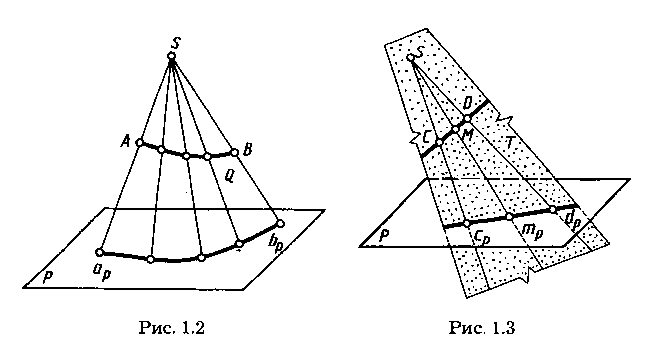
Для обеспечения обратимости чертежа, т. е. однозначного определения положения точки в пространстве по ее проекции, нужны дополнительные условия, например, можно задать второй центр проекций. Центральным проецированием может быть построена проекция любой линии или поверхности как множество проекций всех ее точек (см. рис. 1.2, 1.3). При этом проецирующие прямые (в своей совокупности), проведенные через все точки кривой линии, образуют проецирующую коническую поверхность (рис. 1.2) или могут оказаться в одной плоскости (см. рис. 1.3), которая называется проецирующей.

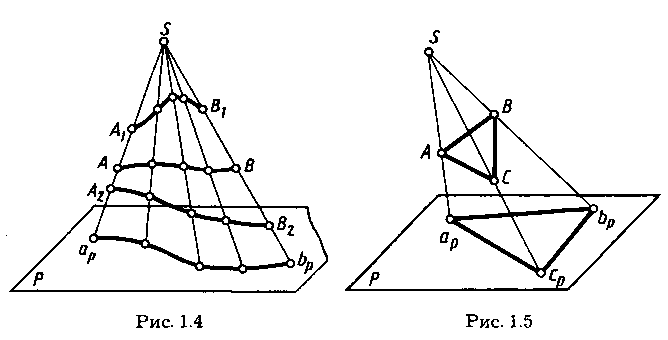
Проекция кривой линии представляет собой линию пересечения проецирующей конической поверхности с плоскостью проекций. Так, на рисунке 1.2 проецирующая коническая поверхностьQ пересекается с плоскостью проекций Р по кривой apbp, являющейся проекцией линии АВ.Однако проекция линии не определяет проецируемую линию, так как на проецирующей поверхности может быть бесчисленное количество линий, проецирующихся в одну и ту же линию на плоскости проекций (рис. 1.4).

При проецировании прямой линии, не проходящей через центр проекций, проецирующей поверхностью служит плоскость. Так, на рисунке 1.3 проецирующая плоскость Т, образуемая проецирующими прямыми SC и SD, проходящими через точки С и D прямой, пересекает плоскость проекций Р по прямой cpdp, которая и является проекцией прямой CD. Соответственно проекциятр точки М прямой CD принадлежит и проекции cpdp.

Для построения проекций линий, поверхностей или тел часто достаточно построить проекции лишь некоторых характерных точек. Например, при построении на плоскости проекций Рпроекции треугольника ABC (рис. 1.5) достаточно построить проекции ар, bр, ср трех его точек — вершин А, В, С.

Свойства центрального проецирования.

1. При центральном проецировании:

а) точка проецируется в точку;

б) прямая, не проходящая через центр проекций, проецируется в прямую (проецирующая прямая — в точку);

в) плоская (двумерная) фигура, не принадлежащая проецирующей плоскости, проецируется в виде двумерной фигуры (фигуры, принадлежащие проецирующей плоскости, проецируются вместе с ней в виде прямой);

г) трехмерная фигура отображается двумерной.

2. Центральные проекции фигур сохраняют взаимную принадлежность, непрерывность и некоторые другие геометрические свойства.

3. При заданном центре проецирования проекции фигуры на параллельных плоскостях подобны.

4. Центральное проецирование устанавливает однозначное соответствие между фигурой и ее изображением, например изображения на киноэкране, фотопленке.

Центральные проекции применяют для изображения предметов в перспективе. Изображения в центральных проекциях наглядны, но для технического черчения неудобны, так как не соблюдается метрика.

2.Параллельные проекции и их основные свойства.

Параллельное проецирование (рис. 1.6) можно рассматривать как частный случай центрального проецирования, при котором центр проекций удален в бесконечность (5оо). При параллельном проецировании применяют параллельные проецирующие прямые, проведенные в заданном направлении относительно плоскости проекций. Если направление проецирования перпендикулярно плоскости проекций, то проекции называют прямоугольными или ортогональными, в остальных случаях— косоугольными (на рис. 1.6 направление проецирования указано стрелкой под углом а не равном 90° к плоскости проекций Р).

При параллельном проецировании сохраняются все свойства центрального проецирования, а также возникают следующие новые свойства.

1. Параллельные проекции взаимно параллельных прямых параллельны, а отношение длин отрезков таких прямых равно отношению длин их проекций.

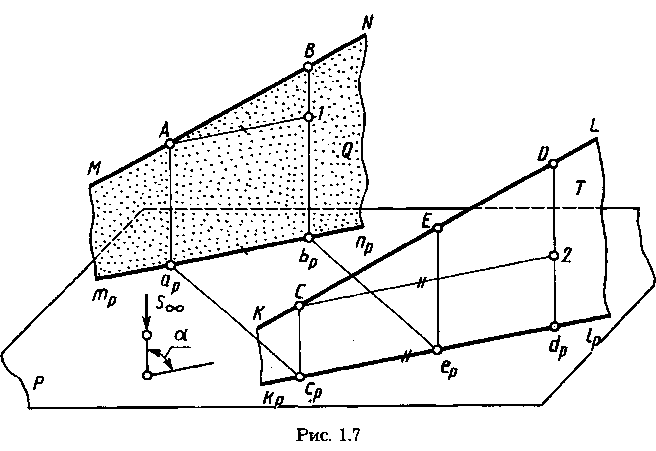
Если прямые MN и KL (рис. 1.7) параллельны, то проецирующие плоскости Q и Т параллельны, так как пересекающиеся прямые в этих плоскостях взаимно параллельны: MN || KL поусловию, Аа_р|| Ссp || S.Следовательно, проекции т_рп_р и k_pl_p параллельны как линии пересечения параллельных плоскостей Q и T с плоскостью Р.

Отметим на прямой MN произвольный отрезок АВ и на прямой KL — произвольный отрезок CD.Проведем в плоскости Q через точку А прямую А—1 || арbр и в плоскости Т через точку С — прямую

C—2 || cpd_p. Отрезки [A—1] = [apb_p], [C—2] = [Cpdp] как отрезки параллельных между параллельными. Отрезки С—2 || с,d_Р || aрb_р и, следовательно, С— 2 || А— 1. Отрезки В— 1 || D—2 || S, треугольник АВ—1 ~ треугольнику CD—2, так как все их стороны взаимно параллельны. Из подобия треугольников АВ— 1 и CD—2 следует:

|АВ|:|CD| = |А—1| : |С—2|= |арbp| : |c_pd_p|

Из рассмотренного следует:

а) если длина отрезка прямой делится точкой в каком-либо отношении, то и длина проекции отрезка делится проекцией этой точки в том же отношении (рис. 1.8):

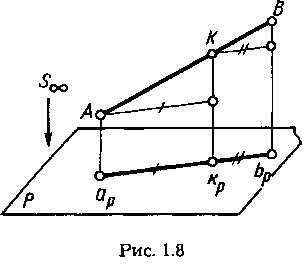
|АК|:|КВ| = |аркр|:|крbр|,

б) проекции равных по длине отрезков взаимно параллельных прямых взаимно параллельны и равны по длине.

Это очевидно, так как (см. рис. 1.7) при |AB|:|CD|=1 будет |арbр| = | c_pd_p|. Поэтому при косоугольном проецировании в общем случае параллелограмм, ромб, прямоугольник, квадрат проецируются в параллелограмм.

2. Плоская фигура, параллельная плоскости проекций, проецируется при параллельном проецировании на эту плоскость в такую же фигуру.

3. Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида и размеров проекции фигуры.

Параллельные проекции, как и центральные при одном центре проекций, также не обеспечивают обратимости чертежа. Применяя приемы параллельного проецирования точки и линии, можно строить параллельные проекции поверхности и тела. Параллельные проекции применяют для построения наглядных изображений различных технических устройств и их деталей, например аксонометрических проекций, рассматриваемых ниже.

2. Прямоугольное (ортогональное ) проецирование.

Частный случай параллельного проецирования, при котором направление проецирования перпендикулярно плоскости проекций, называют прямоугольным или ортогональным проецированием. Прямоугольной (ортогональной) проекцией точки называют основание перпендикуляра, проведенного из точки на плоскость проекций. Прямоугольная проекция d_pточки D показана на рисунке 1.9.

Наряду со свойствами параллельных (косоугольных) проекций ортогональное проецирование имеет следующее свойство:

ортогональные проекции двух взаимно перпендикулярных прямых, одна из которых параллельна плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны.

Докажем это. На рисунке 1.10 угол АВС= 90°; (АВ) || Р; (СВ) не перпендикулярно Р. Докажем, что угол арbрср= 90°.

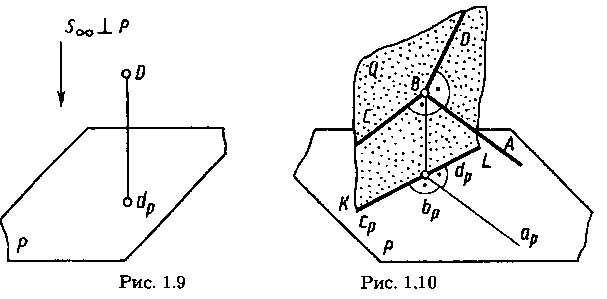Проецирующая прямая Вь, перпендикулярна плоскости проекций Р и прямой ВА. Прямая ВАперпендикулярна плоскости Q (Q включает Bbp; Q включает BC), так как прямая ВАперпендикулярна двум пересекающимся прямым этой плоскости (а угол ABbp = 90° — по условию, а угол АВb_Р= 90° — по построению). Проекция bpap перпендикулярна плоскости Q, так как (bpap) || (ВА). Следовательно, проекция плоскости Q на плоскости Р — прямая KL,перпендикулярная проекции bpap. Но с прямой KL совпадает проекция ь_рс_р, т. е. угол арb_рс_р=90°, что и требовалось доказать.

Соответственно при угле DBA = 90°, (DB) не перпендикулярно Р и (АВ) || Р имеем:

угол dpbpap= 90°.

Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием. К ним, в первую очередь, относятся простота геометрических построений ортогональных проекций точек и сохранение на проекциях при определенных условиях формы и размеров проецируемой фигуры.

Указанные преимущества обеспечили применение ортогонального проецирования для разработки чертежей во всех отраслях промышленности и в строительстве.

3. Проецирование на три взаимно перпендикулярные плоскости проекций.

Обратимость чертежа может быть обеспечена проецированием на две непараллельные плоскости проекций.

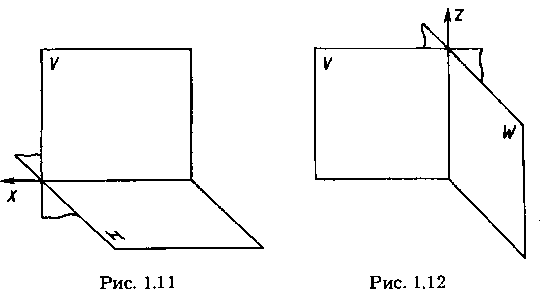
Для удобства проецирования в качестве двух плоскостей проекций выбирают две взаимно перпендикулярные плоскости (рис. 1.11). Одну из них принято располагать горизонтально — ее называют горизонтальной плоскостью проекций, другую — вертикально. Вертикальную плоскость называют фронтальной плоскостью проекций. Эти плоскости проекций пересекаются по линии, называемой осью проекций.

Ось проекций разделяет каждую из плоскостей проекций на две полуплоскости.

Обозначим плоскости проекций буквами: V — фронтальную, Н — горизонтальную, ось проекций — буквой х или в виде

дроби V/H. Плоскости V и Н образуют систему V, Н. (Наряду с указанными обозначениями плоскостей проекций в литературе применяют и другие обозначения, например буквой π с индексами.)

Плоскости проекций, пересекаясь, образуют четыре двугранных угла, из которых приведенный на рисунке 1.11 (с обозначениями граней V, Н) считают первым.

В промышленности чертежи многих деталей выполняют также в системе двух взаимно перпендикулярных плоскостей, пересекающихся по вертикальной оси проекций z (рис. 1.12). При этом фронтальной плоскостью проекций оставляют также плоскость V, а перпендикулярную к ней и обозначаемую W называют профильной плоскостью проекций.

В системе двух взаимно перпендикулярных плоскостей проекций горизонтальной проекцией точки называют прямоугольную проекцию точки на горизонтальной плоскости проекций;

фронтальной проекцией точки называют прямоугольную проекцию точки на фронтальной плоскости проекций.

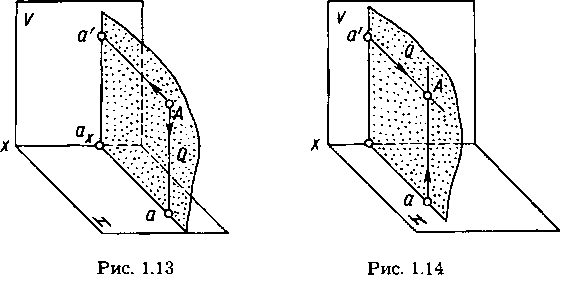
Наглядное изображение построения проекций произвольной точки А в системе V, Н показано на рисунке 1.13. Горизонтальную проекцию, обозначенную а, находят как пересечение перпендикуляра, проведенного из точки А к плоскости Н, с этой плоскостью. Фронтальную проекцию, обозначенную а', находят как пересечение перпендикуляра, проведенного из точки А к плоскости V, с этой плоскостью.

Проецирующие прямые Аа' и Аа, перпендикулярные к плоскостям V и Н, принадлежат плоскостиQ. Она перпендикулярна плоскостям проекций и пересекает ось проекций в точке а_х. Три взаимно перпендикулярные плоскости Q, V и Н пересекаются по взаимно перпендикулярным прямым, т. е. прямые а'а_х, аа_х и ось х взаимно перпендикулярны.

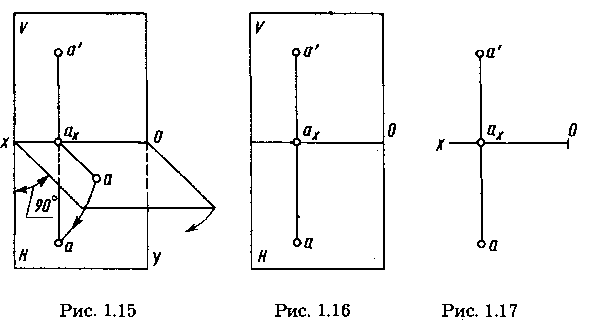
Построение некоторой точки А в пространстве по двум заданным ее проекциям — фронтальной а'и горизонтальной а — показано на рисунке 1.14. Точку А находят на пересечении перпендикуляров, проведенных из проекции а' к плоскости V и из проекции а к плоскости Н.Проведенные перпендикуляры принадлежат одной плоскости Q, перпендикулярной к плоскостямV и Н, и пересекаются в единственной искомой точке А пространства.

Таким образом, две прямоугольные проекции точки вполне определяют ее положение в пространстве относительно данной системы взаимно перпендикулярных плоскостей проекций.

В дальнейшем прямоугольные проекции точки в системе взаимно перпендикулярных плоскостей проекций будем называть ортогональными проекциями точки.

Рассмотренное наглядное изображение точки в системе V, Н неудобно ввиду своей сложности для целей черчения. Преобразуем его так, чтобы горизонтальная плоскость проекций совпадала с фронтальной плоскостью проекций, образуя одну плоскость чертежа. Это преобразование осуществляют (рис. 1.15) путем поворота вокруг оси х плоскости Н на угол 90° вниз. При этом отрезки а_х= а' и а_х = а образуют один отрезок а'а, перпендикулярный оси проекции, называемыйлинией связи. В результате указанного совмещения плоскостей V и Н получается чертеж — рисунок 1.16, известный под названием эпюр (от французского ериrе — чертеж, проект) или эпюр Монжа. Этот чертеж в системе V, Н (или в системе двух прямоугольных проекций) называют чертежом Монжа. Без обозначения плоскостей V и H этот чертеж приведен на рис. 1.17.