Преобразование поворота
Преобразование поворота, также как и при рассмотрении плоских геометрических объектов, позволяет поворачивать исходное изображение на заданный угол. Поворот осуществляется вокруг центра изображения. При этом возможны два варианта поворота:
1. Области изображения, вышедшие за его границы при повороте отсекаются, а незаполненные части заполняются каким-либо цветом.
2. Рассчитывается новый размер изображения на основе угла поворота таким образом, чтобы повёрнутое изображение целиком поместилось в новые размеры. Незаполненные части изображения также заполняются каким-либо цветом.
В любом случае для расчёта преобразования поворота может быть использована следующая формула:
Cnew[i][j] = 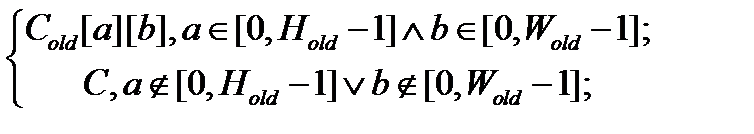
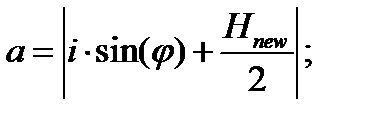
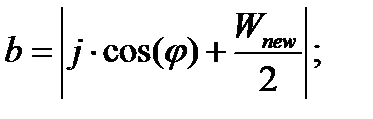
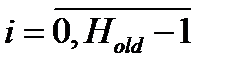 ,
, 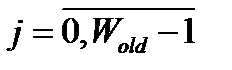 .
.
В этой формуле параметр C определяет цвет, которым заполняются пустые участки изображения. Параметр φ определяет угол поворота по часовой стрелке в радианах.
Приведённая формула округляет преобразованные координаты. Однако можно использовать и билинейную интерполяцию, когда цвет пикселя вычисляется как взвешенная сумма цветов четырёх соседних пикселей.
Цифровые фильтры изображений
Цифровые фильтры позволяют накладывать на изображение различные эффекты, например: размытие, резкость, деформацию, шум и т. д.
Цифровой фильтр представляет собой алгоритм обработки изображения. Большая группа цифровых фильтров имеет один и тот же алгоритм, но эффект, накладываемый фильтром на изображение, зависит от коэффициентов, используемых в алгоритме.
Фильтрация изображений является одной из самых фундаментальных операций компьютерного зрения, распознавания образов и обработки изображений. Фактически, с той или иной фильтрации исходных изображений начинается работа подавляющего большинства методов.
Линейные фильтры
Линейные фильтры представляют собой семейство фильтров, имеющих очень простое математическое описание. Вместе с тем они позволяют добиться самых разнообразных эффектов. Будем считать, что задано исходное полутоновое изображение A, и обозначим интенсивности его пикселей A(x, y). Линейный фильтр определяется вещественнозначной функцией F, заданной на растре. Данная функция называется ядром фильтра, а сама фильтрация производится при помощи операции дискретной свертки[1] (взвешенного суммирования):
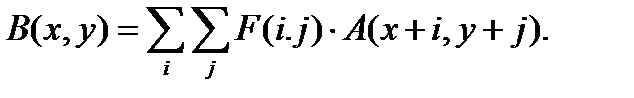
Результатом служит изображение B. В приведенной формуле не определены пределы суммирования. Обычно ядро фильтра отлично от нуля только в некоторой окрестности N точки (0, 0). За пределами этой окрестности F(i, j) или в точности равно нулю, или очень близко к нему, так что можно им пренебречь. Поэтому суммирование производится по (i, j) Є N, и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (обозначим это множество N(x, y)). Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m×n, где длины сторон являются нечетными числами. При задании ядра матрицей Mkl, ее следует центрировать:
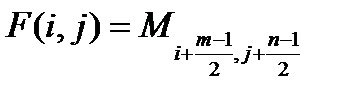
Также нуждается в дополнительном прояснении ситуация, когда пиксель (x, y) находится в окрестности краев изображения. В этом случае A(x+i, y+j) может соответствовать пикселю A, лежащему за границами изображения A. Данную проблему можно разрешить несколькими способами:
§ не проводить фильтрацию для таких пикселей, обрезав изображение B по краям или закрасив их, к примеру, черным цветом;
§ не включать соответствующий пиксель в суммирование, распределив его вес F(i, j) равномерно среди других пикселей окрестности N(x, y);
§ доопределить значения пикселей за границами изображения при помощи экстраполяции;
§ доопределить значения пикселей за границами изображения, при помощи зеркального отражения.
Выбор конкретного способа нужно производить с учетом конкретного фильтра и особенностей конкретного приложения. Разобрав общее определение линейных фильтров, перейдем к примерам.
Сглаживающие фильтры
Результатом применения сглаживающего фильтра является размытие изображения, устранение резких цветовых переходов. Простейший прямоугольный сглаживающий фильтр радиуса r задается при помощи матрицы размера (2r + 1) × (2r + 1), все значения которой равны:
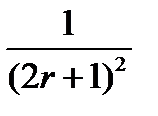 ,
,
а сумма по всем элементам матрицы равна, таким образом, единице. При фильтрации с данным ядром значение пикселя заменяется на усредненное значение пикселей в квадрате со стороной 2r+1 вокруг него. Пример фильтрации при помощи прямоугольного фильтра приведен на рис. 4.19.
 а) а) | 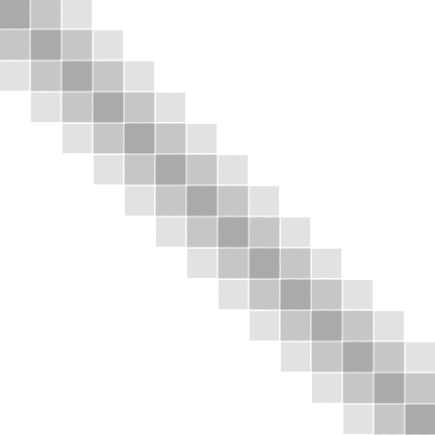 б) б) |
Рис. 4.19. Пример использования сглаживающего фильтра
В этом случае на исходное изображение (рис. 4.19, а) наложен прямоугольный фильтр размером 3 на 3 пикселя. Ядро фильтра в этом случае выглядит следующим образом:
 .
.
Результат фильтрации приведен на изображении справа (рис. 4.19, б). Отметим, что сумма всех элементов ядра фильтра дает в результате единицу. Потому можно сказать, что при использовании такого фильтра в целом яркость всего изображения не меняется. Однако, в следствии усреднения значений цветов пикселей, контрастность изображения уменьшается, что и видно на рис. 4.19.
Как видим из приведенного примера, сглаживающие фильтры могут применяться для устранения лестничного эффекта, а также для шумоподавления.
Шум – дефект на изображении, вносимый фотосенсорами и электроникой устройств, или возникающий при использовании аналоговых устройств. Шум на изображении проявляется в виде случайным образом расположенных элементов растра (точек), имеющих размеры близкие к размеру пикселя. Шум отличается от изображения более светлым или тёмным оттенком серого и цвета и/или по цвету. Причиной появления шумов на изображении является: зернистость плёнки, грязь, пыль, царапины, отслоение фотографической эмульсии. Если рассматривать цифровые устройства то причиной возникновения цифрового шума является: тепловой шум матрицы, шум переноса заряда, шум квантования АЦП, усиление сигналов в цифровом фотоаппарате, грязь, пыль на сенсоре.
Применение линейной фильтрации с прямоугольным ядром имеет существенный недостаток: пиксели на расстоянии r от обрабатываемого оказывают на результат тот же эффект, что и соседние. Более эффективное шумоподавление можно осуществить, если влияние пикселей друг на друга будет уменьшаться с расстоянием. Этим свойством обладает гауссовский фильтр с ядром:
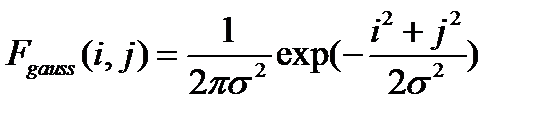
Гауссовский фильтр имеет ненулевое ядро бесконечного размера. Однако ядро фильтра очень быстро убывает к нулю при удалении от точки (0, 0), и потому на практике можно ограничиться сверткой с окном небольшого размера вокруг (0, 0) (например, взяв радиус окна равным 3σ).
Гауссовская фильтрация также является сглаживающей. Однако, в отличие от прямоугольного фильтра, образом точки при гауссовой фильтрации будет симметричное размытое пятно, с убыванием яркости от середины к краям, что гораздо ближе к реальному размытию от расфокусированных линз.
