Теорема о жестком рычаге Н.Е. Жуковского

ЛЕКЦИЯ 6

Краткое содержание

Силовой расчет начального механизма. Определение уравновешивающей силы и уравновешивающего момента. Теорема Н.Е. Жуковского о жестком рычаге.

Силовой расчет начального механизма

Начальный механизм состоит из ведущего звена, которое входит во вращательную или поступательную кинематическую пару со стойкой.

Кинематическая цепь будет статически определима при условии 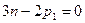. Начальный механизм при n = 1 и p₁ = 1 не будет находиться в равновесии. Для того, чтобы начальный механизм находился в равновесии, необходимо дополнительно ввести уравновешивающую силу 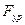или уравновешивающий момент 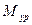, которые бы уравновесили все силы и моменты, приложенные к ведущему звену.

Уравновешивающая сила 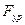или уравновешивающий момент 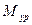являются такой силой или моментом, которые должны быть приложены к ведущему звену, чтобы механизм двигался по заданному закону или удерживался в заданном положении.

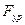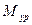Что действует на ведущее звено или - зависит от способа передачи энергии от электродвигателя к валу кривошипа. Возможны следующие случаи.

1. Коленчатый вал двигателя соединяется с валом рабочей машины муфтой (рис.6.1). В этом случае к валу приложен уравновешивающий момент .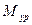

Электродвигатель.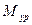

рис. 6.1.

Пример 6.1

Дано:

Масса звена: m₁=2 кг. Ускорения центра масс звена:, 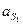= 2,95 м/с².

1).Определение силы тяжести звена:

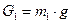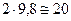= н.

2).Определение силы инерции:

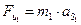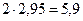= н.

Сила инерции направлена в противоположную сторону ускорению .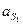

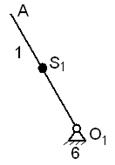
Построим начальный механизм в масштабе 1:5.

Покажем все действующие на него силы, неизвестную реакцию R₆₁ и уравновешивающий момент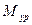

1.Найдем величину уравновешивающего момента .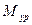

Запишем уравнение моментов всех сил относительно точки О₁.

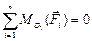
План сил для начального механизма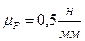

Уравновешивающий момент 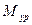равен:

Здесь 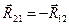. Длины плеч h₁ и h₂ измерены на расчетной схеме и умножены на масштаб.

2.Найдем реакцию R₆₁.

Составим векторное уравнение равновесия всех сил, действующих на начальный механизм.

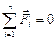
Выберем масштаб плана сил m_F= 0,5 .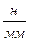

Вычислим величины отрезков, соответствующих векторам сил. Данные занесем в таблицу 1:

Таблица 1

Обозначение силы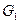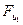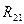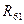
Величина силы, н
Отрезок на плане, мм

Строим план сил. В соответствии с векторным уравнением откладываем отрезки, соответствующие векторам 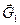, , 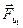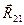. Векторы можно откладывать в любом порядке. Соединяя начало первого вектора и конец последнего, получим многоугольник сил и отрезок, определяющий реакцию 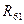. Измеряя его длину и умножая на масштаб m_F, получим величину реакции 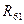. Данные занесены в таблицу 1.

2.Вал двигателя соединяется с валом рабочей машины при помощи зубчатой передачи (рис.6.2). В этом случае к валу двигателя приложена уравновешивающая сила, которая действует по линии зацепления.

Зубчатый

Электродвигатель механизм

Рис. 6.2

Пример 6.2.

Дано:

Масса звена: m₁=2 кг. Ускорения центра масс звена:, 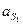= 2,95 м/с².

1).Определение силы тяжести звена:

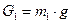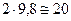= н.

2).Определение силы инерции:

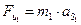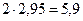= н.

Сила инерции направлена в противоположную сторону ускорению .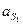

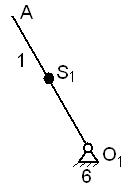
Построим начальный механизм в масштабе 1:5.

Покажем все действующие на него силы, неизвестную реакцию R₆₁ и уравновешивающую силу F_ур, которую приложим перпендикулярно кривошипу АО₁ в точке А.

План сил для начального механизма

1.Найдем величину уравновешивающей силы F_ур.

Запишем уравнение моментов всех сил относительно точки О₁.

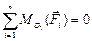
Уравновешивающая сила F_ур равна:

Здесь 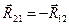. Длины плеч h₁ и h₂ измерены на расчетной схеме и умножены на масштаб.

2.Найдем реакцию R₆₁.

Составим векторное уравнение равновесия всех сил, действующих на начальный механизм.

.

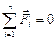Выберем масштаб плана сил m_F=0,5 .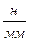

Вычислим величины отрезков, соответствующих векторам сил. Данные занесем в таблицу 2:

Таблица 2

Обозначение силы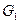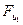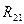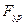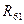
Величина силы, н
Отрезок на плане, мм

Строим план сил. В соответствии с векторным уравнением откладываем отрезки, соответствующие векторам 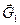, , 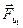, 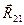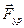. Векторы можно откладывать в любом порядке. Соединяя начало первого вектора и конец последнего, получим многоугольник сил и отрезок, определяющий реакцию 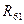. Измеряя его длину и умножая на масштаб m_F, получим величину реакции 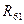. Данные занесены в таблицу 2.

Теорема о жестком рычаге Н.Е. Жуковского

Н.Е.Жуковский показал, что равновесию механизма с одной степенью свободы соответствует равновесие некоторого рычага, и предложил способ построения и нагружения такого рычага. Теорему Н.Е.Жуковского можно сформулировать так:

Если векторы всех сил, приложенных к различным точкам звеньев и уравновешенных на механизме, перенести параллельно самим себе в одноимённые точки повёрнутого на 90° плана скоростей, приняв фигуру плана за жесткий рычаг, то сумма моментов всех указанных сил относительно полюса плана будет равна нулю.

Пример 6.3.

Для кривошипно-ползунного механизма определить уравновешивающую силу .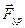

Решение.

1.Уравновешивающую силу 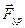приложим в точке А перпендикулярно кривошипу АО. Построим

план скоростей и повернем его на 90°. В соответствующих точках плана скоростей приложим векторы сил, сохраняя их направления, момент 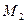заменим парой сил 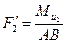и каждую силу перенесем на план.

2.Составим уравнение моментов всех сил относительно полюса :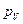

.

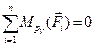Решая уравнение, получим:

Длины всех плеч измерены на расчетной схеме .

План скоростей, повернутый на 90^○

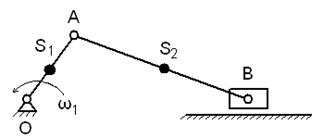
План скоростей

Таким образом, с помощью теоремы Жуковского можно:

1.Определить уравновешивающую силу 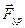, не проводя силового расчета;

2.Проверить значение уравновешивающей силы 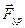, полученной из силового расчета. Погрешность расчетов составляет 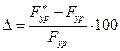%. Погрешность не должна превышать 20 %.