Примеры построения точек пересечения прямой с поверхностью
Пример: Построить точки пересечения прямой АВ с конусом (рис. 76 а, б).
Через прямую АВ проводят плоскость α общего положения, из условия, чтобы она пересекла конус по образующим. Следовательно, она должна пройти через вершину конуса.
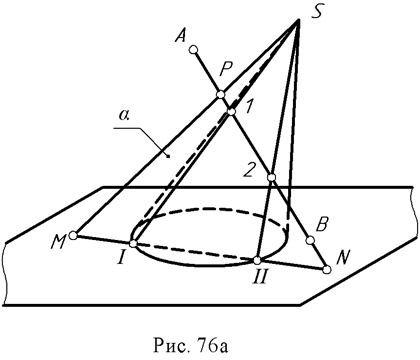
Введенная плоскость определяется пересекающимися прямыми АВ и РS, точка Р взята произвольно на АВ. Линия сечения плоскости с конусом - это образующие SI и SII, которые находят при помощи линии MN, являющейся линией пересечения (следом) плоскостей аи П1, т.е. с той плоскостью, в которой расположено основание конуса. Точки 1 и 2 - точки пересечения линии АВ с конусом - определяют как пересечение образующих SI и SII с прямой АВ.
Решение задачи на комплексном чертеже (рис. 76б).
1. Через прямую АВ проводят плоскость α(АВ∩PS; PÎAB).
2. Строят линию пересечения плоскости ас конусом - образующие SI и SII.
3. Отмечают точки пересечения образующих SI и SII с АВ - точки 1 и 2.
4. Определяют видимость точек 1 и 2 и видимость прямой АВ относительно конуса.
В случае, когда один из геометрических образов, участвующих в пересечении является проецирующим, задача сводится к задаче на принадлежность.
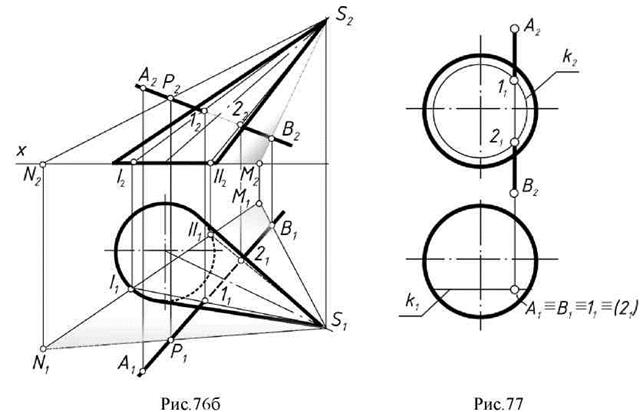
Пример: Определить точки пересечения прямой АВ со сферой (рис. 77).
Прямая АВÖП1, следовательно, точки пересечения АВ со сферой на горизонтальной проекции совпадут с проекцией прямой - это точки 11 и 21. Определить фронтальные их проекции можно с помощью окружности к.
Вопросы для самопроверки.
1. Укажите общую схему определения точек пересечения прямой с поверхностью.
2. Укажите, какие могут быть случаи пересечения прямой с поверхностью.
3. Как выбирают плоскость-посредник при построении линии пересечения прямой с поверхностью?
Лекция 11. Взаимное пересечение поверхностей.
Общие положения.
При взаимном пересечении поверхностей геометрических тел, следует различать два вида пересечения.
К первому виду относятся пересечения, когда все образующие или ребра боковой поверхности одного из тел участвуют в пересечении с поверхностью
другого тела. Такой вид пересечения называется полным. Из рис. 78а видно, что все образующие цилиндра G пересекаются с поверхностью цилиндра Ф.
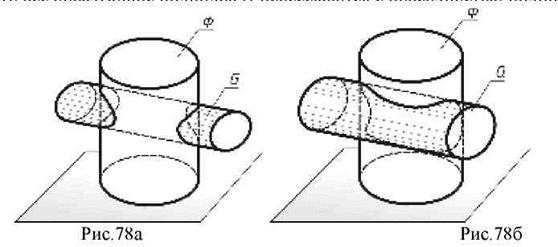
Ко второму виду относятся пересечения, при которых у обоих пересекающихся геометрических тел имеются образующие или ребра боковых поверхностей, не участвующих в пересечении. Такой вид пересечения называется частичным (или неполным) (рис.78б).
При полном пересечении образуются две замкнутые линии пересечения (рис. 78а), а при частичном – одна (рис. 78б).
Если пересекаются две кривые поверхности, то линия пересечения является замкнутой плавной кривой. При пересечении поверхности гранного тела с кривой поверхностью второго тела линия пересечения представляет собой замкнутую линию, отдельные участки которой являются плавными кривыми, сочлененными друг с другом в точках, расположенных на участвующих в пересечении ребрах гранного тела.
В случае пересечения поверхностей двух гранных тел линия пересечения будет представлять собой пространственную замкнутую ломаную линию с точками перелома на ребрах, участвующих в пересечении.
Линия пересечения двух поверхностей состоит из ряда точек, принадлежащих одновременно обеим поверхностям (рис. 78в). Нахождение этой линии осуществляется по следующей схеме:
1. Заданные поверхности пересекают вспомогательной плоскостью, называемой посредником - α.
Строят линии пересечения посредника с заданными поверхностями:
к1 = Ф1 Ç α; к2 = Ф2Ç α
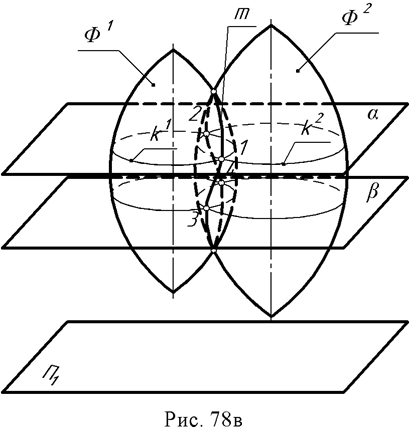
3. Отмечают точки пересечения полученных линий, которые и являются точками линии пересечения заданных поверхностей 1, 2 = к1 Ç к2
Повторив построение с использованием нескольких посредников, определяют ряд точек линии пересечения 3, 4 … Полученные точки соединяют и получают искомую линию пересечения двух поверхностей: m= Ф1 Ç Ф2.
Плоскости - посредники выбирают таким образом, чтобы в сечении получались простейшие линии. Это, как правило, для поверхностей вращения - окружности, а для линейчатых поверхностей - образующие.
Если с использованием плоскостей - посредников это осуществить невозможно, используют в качестве посредника сферу. В зависимости от вида посредника различают следующие способы построения линий пересечения поверхностей:
1. Способ вспомогательных плоскостей общего положения;
2. Способ вспомогательных проецирующих плоскостей;
3. Способ вспомогательных сфер.
Каким бы способом не производилось построение, при нахождении точек линии пересечения двух поверхностей необходимо соблюдать определенную последовательность. Линия будет складываться из опорных и случайных точек. Начинают построения с нахождения опорных точек. Линия пересечения должна находиться в пределах области наложения проекций поверхности.
