Пересечение поверхности вращения плоскостью

Рассмотрим примеры построения линии пересечения поверхностей вращения плоскостью. При построении сечений следует выделить частный случай, когда секущая плоскость является проецирующей или пересекаемая поверхность занимает проецирующее положение.

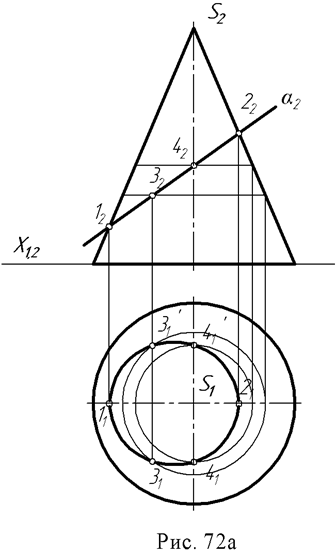
Пример 1. Построить пересечение конуса проецирующей плоскостью α (рис. 72а).

Секущая плоскость является фронтально – проецирующей, поэтому фронтальная проекция линии пересечения лежит на следе плоскости (α₂) и полученный в сечении эллипс проецируется на плоскость П₂ отрезком прямой 1₂ – 2₂.

Горизонтальная проекция точек эллипса строится с помощью параллелей конуса.

Пример 2. Построить линию пересечения конуса плоскостью общего положения (рис. 72б).

Эта задача сложнее предыдущей, так как здесь отсутствуют проецирующие элементы, поэтому необходимо построить обе проекции линии сечения. Решение этой задачи может быть выполнено двумя способами.

Первый способ (рис. 72б) – рассекаем поверхность и плоскость плоскостями посредниками частного положения, применяя изложенный выше алгоритм.

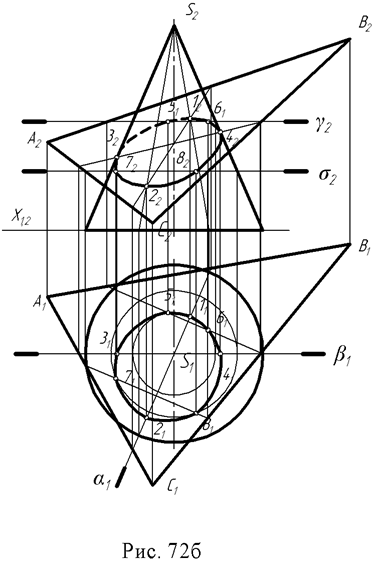
Сначала необходимо определить характерные (опорные) точки сечения:

1. Точки высшую и низшую (1 и 2), лежащие на оси симметрии сечения, определяют, рассекая плоскость и поверхность плоскостью α (α₁), проходящей через линию ската (линию наибольшего наклона) заданной плоскости и через ось конуса;

2. Точки видимости, лежащие на очерковых образующих и разделяющие видимую и невидимую часть линии сечения – это точки 3 и 4, полученные с помощью секущей плоскости β (β₁), проходящей параллельно плоскости П₂ и через ось конуса;

3.Промежуточные точки – 5, 6, 7, 8 – которые получаются при рассечении поверхности и данной плоскости горизонтальными плоскостями - посредниками γ (γ₂), σ (σ₂).

Через построенные проекции точек линии сечения проводится плавная кривая – эллипс. Рассмотренный пример дает представление об общем методе построения линии пересечения поверхности плоскостью.

Второй способ (рис. 72в).

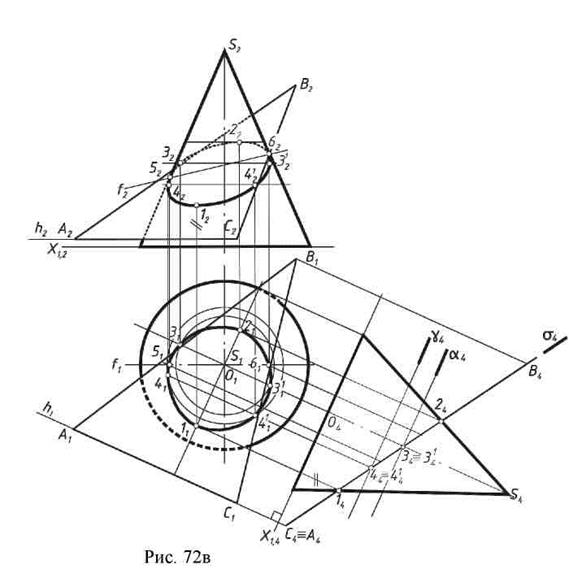
Он заключается в преобразовании чертежа замененной фронтальной плоскости проекций, при котором заданная плоскость общего положения преобразуется во фронтально - проецирующую. Новая ось Х_1,,4 и плоскость П₄ проводится перпендикулярно горизонтальной проекции горизонтали заданной плоскости (Х_{1, 4} Öh₁). Высшая и низшая точки 1₄ и 2₄ определяются на пересечении плоскости, вырожденной в линию σ₄ с новым очерком конуса.

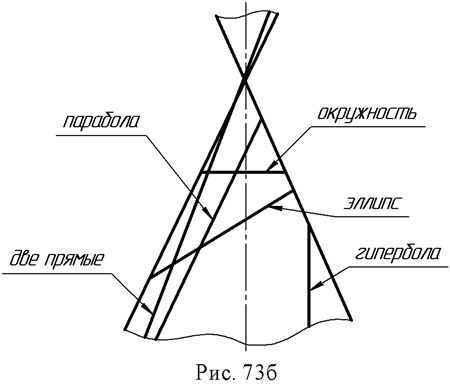
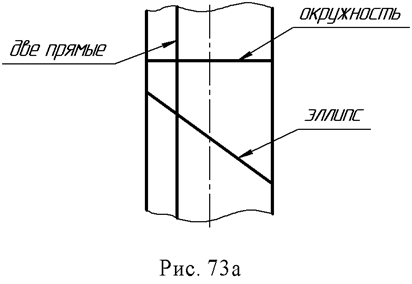
Часто заранее известен вид кривой, получающейся в сечении поверхности плоскостью. Так, сфера пересекается плоскостью всегда по окружности, цилиндр вращения пересекается плоскостью, в общем случае по эллипсу. Если же секущая плоскость параллельна или перпендикулярна оси цилиндра, то в сечении получается соответственно две образующие или окружность (рис. 73а).

В сечении конуса вращения получаются все виды кривых второго порядка (конические сечения).

Если секущая плоскость не параллельна ни одной из образующих конуса, т.е. пересекает все образующие, то в сечении получается эллипс.

Если секущая плоскость перпендикулярна оси конуса, то получится окружность. Если секущая плоскость параллельна одной образующей конуса, то в сечении получается парабола. Если секущая плоскость параллельна двум образующим, то в сечении получается гипербола. В частности, если плоскость проходит через вершину конуса, в сечении получаются две образующие (рис. 73б).