Основные графические способы построения разверток поверхностей

1. Способ треугольников (триангуляции).

Этот способ применяют для построения разверток гранных и всех развертывающихся линейчатых поверхностей. Способ триангуляции для этих поверхностей универсален.

Сущность способа заключается в том, что кривую линейчатую поверхность заменяют вписанной в нее многогранной с треугольными гранями, нахождению натурального вида их и последовательному построению на чертеже.

Пример: Построить развертку эллиптического конуса, заданного круговым основанием с вершиной S (рис. 89а,б).

Впишем в заданный конус двенадцатигранную пирамиду, имеющую в основании правильный 12-угольник. Далее заменим дуги основания хордами и определим ошибку этой замены. Она составит: .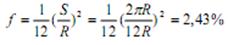

Поверхность имеет плоскость симметрии, которая проходит через ось конуса параллельно фронтальной плоскости проекций. Поэтому можно построить развертку для половины поверхности. Способом прямоугольного треугольника определяем натуральные величины сторон треугольников S1, S2 …

Так как превышение точки S над точками 1, 2, 3 и т.д. постоянная величина Z^S, то прямоугольный треугольник строим на фронтальной проекции. Один катет ∆Z=Z^S, а второй - длина горизонтальной проекции отрезков (S₁1₁, S₁2₁ … и т.д.).

Гипотенузы прямоугольных треугольников дают натуральные величины отрезков S1, S2 и т.д. Натуральные величины отрезков А1, 12, 23 и т.д. можно замерить на горизонтальной проекции, т.к. они параллельны этой плоскости, т.е. А1 = А₁1₁; 12=1₁2₁ и т.д. Затем каждый треугольник графически строят по трем сторонам, один примыкает к другому. На произвольной линии откладываем отрезок А₀S₀= /AS / = A₂S₂ и на нем достраиваем треугольник со сторонами S1 и А1 (из точки S₀ проводят дугу радиуса S1, а из точки А₀ - дугу радиуса А1, в пересечении этих дуг получена точка 1₀).

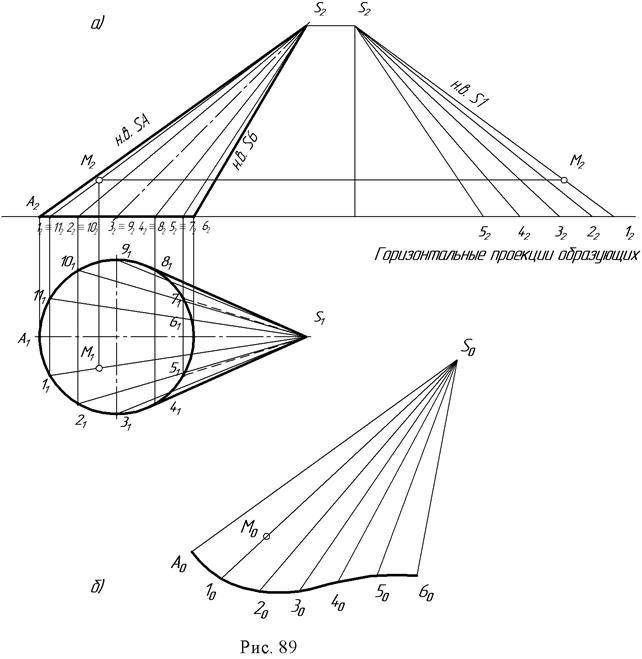
Все последующие треугольники строятся аналогично, после чего через точки развернутого по способу хорд основания конуса проводят по лекалу плавную линию. Надо обратить внимание на одну из опорных точек развертки окружности основания конуса точку 4₀. Она является точкой перегиба и получается из той точки основания, через которую проходит образующая поверхности, являющаяся линией границы видимого контура по отношению к плоскости основания конуса (рис. 89б).

Фактически на рис. 89 построена развертка пирамидальной поверхности.

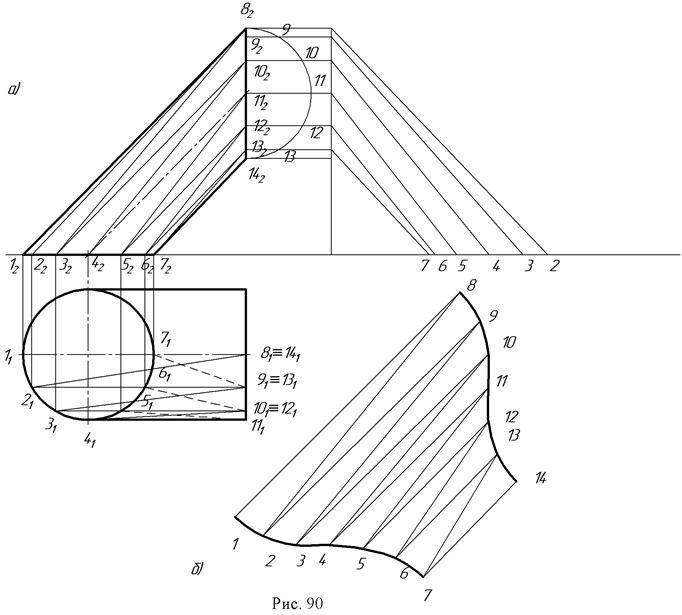
Пример 2. Построить развертку поверхности цилиндроида (рис. 90а,б).

Заменяется данная поверхность вписанной в нее многогранной поверхностью, так же состоящей из треугольников: строятся натуральные величины этих треугольников так же, как это было сделано в примере 1, и, проведя через их вершины по лекалу плавные кривые, получаем приближенную развертку поверхности цилиндроида (рис. 90б).

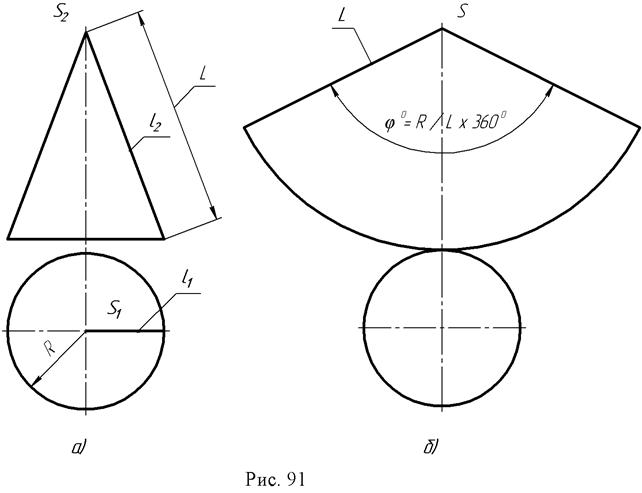
Для развертывания боковой поверхности прямого кругового конуса (рис. 91) используется известное из стереометрии построение с подсчетом угла сектора, представляющего собою искомую развертку φ₀ = R/L x 360º , где R - это радиус основания конуса, L - длина его образующей.

Способ нормального сечения (рис. 92) используется для построения развертки призматических и цилиндрических поверхностей.

Построение разверток указанных поверхностей приводит, в общем случае, к многократному построению натурального вида трапеций и параллелограммов, из которых состоит данная призматическая поверхность или призматическая поверхность, описанная или вписанная в данную цилиндрическую поверхность и заменяющая её.

Построение трапеций или параллелограммов производится по их основаниям и высотам, причем необходимо знать отрезки оснований, на которые они делятся высотами (рис. 92).

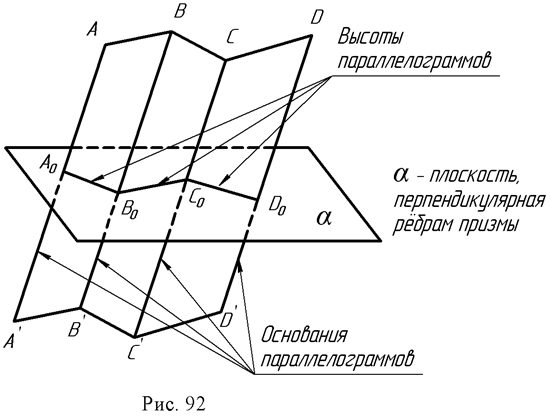
Поэтому для построения развертки необходимо предварительно пересечь поверхность плоскостью, перпендикулярной к ребрам. Стороны этого сечения и будут высотами трапеций или параллелограммов, из которых состоит поверхность.

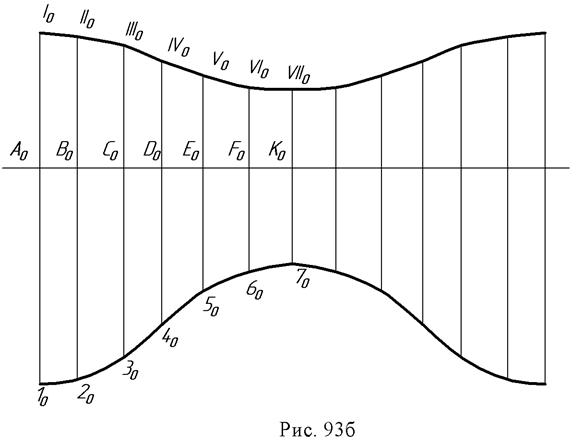
Пример: Построить развертку поверхности эллиптического цилиндра (рис. 93а).

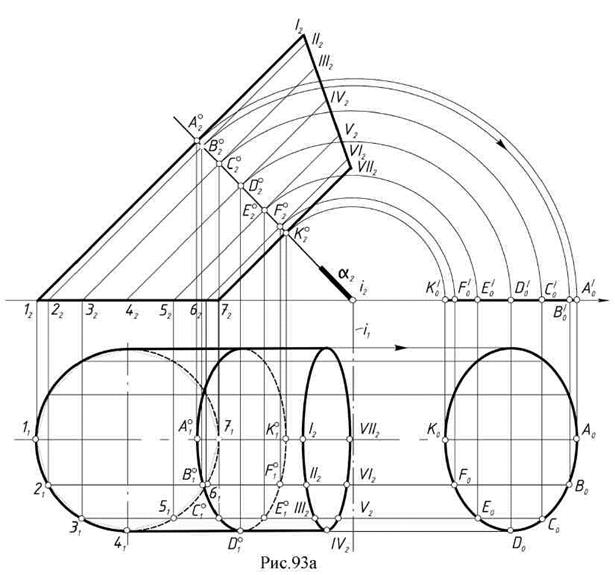
В заданную поверхность вписана 12-угольная призма, для чего основание цилиндра разделено на 12 равных частей и проведены ребра параллельно образующим цилиндра. Проводим плоскость нормального сечения а(а₂) перпендикулярно фронтальным проекциям образующих и строим проекции (А₁, В₁, С₁, D₁ … и А₂, В₂, С₂) и натуральную величину нормального сечения А₀, В₀, С₀, D₀ … (способом вращения вокруг проецирующей оси i).

На произвольной горизонтальной линии откладываем отрезки А₀В₀, В₀С₀, С₀D₀, D₀Е₀ … и т.д. Через полученные точки А_0,, В₀, С₀ и т.д. проводим перпендикуляры, на которых откладываем длины ребер (образующих, взятые с фронтальной проекции, так как они являются фронталями (рис. 93б). Точки I₀, II₀, III₀ и т.д. - развертка окружности верхнего основания; 1₀, 2₀, 3₀ и т.д. - развертка окружности нижнего основания цилиндра.

Полученная фигура является разверткой боковой поверхности цилиндра. Построение разверток призматических поверхностей производится аналогично.