Контрастоповышающие фильтры
Если сглаживающие фильтры снижают локальную контрастность изображения, размывая его, то контрастоповышающие фильтры производят обратный эффект. Ядро контрастоповышающего фильтра имеет значение, большее 1, в точке (0, 0), при общей сумме всех значений, равной 1.
Например, контрастоповышающим фильтром является фильтр с ядром, задаваемым матрицей:
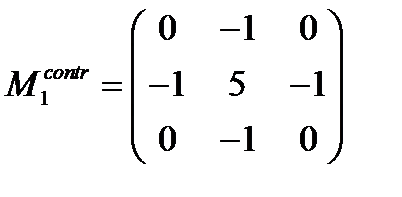
либо матрицей:
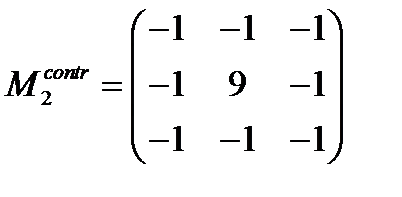
Эффект повышения контраста достигается за счет того, что фильтр подчеркивает разницу между интенсивностями соседних пикселей, удаляя эти интенсивности друг от друга (рис. 4.20). Этот эффект будет тем сильней, чем больше значение центрального члена ядра. Результат работы фильтра на исходном изображении (рис. 4.20, а) для 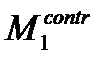 представлен на рис. 4.20, б, для
представлен на рис. 4.20, б, для 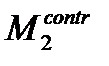 на рис. 4.20, в.
на рис. 4.20, в.
 а) а) | 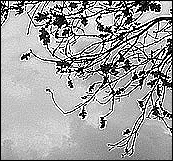 б) б) | 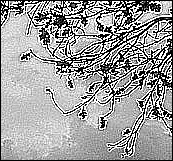 в) в) |
Рис. 4.20. Пример использования контарстноповышающего фильтра
Характерным артефактом линейной контрастоповышающей фильтрации являются заметные светлые и менее заметные темные ореолы вокруг границ.
Разностные фильтры
Разностные фильтры часто используются для нахождения границ в изображениях. При этом используют дифференциальный оператор, вычисляющий приближенное значение градиент[2] яркости изображения. Результатом применения такого оператора в каждой точке изображения является либо вектор градиента яркости в этой точке, либо его норма.
Результат показывает, насколько «резко» или «плавно» меняется яркость изображения в каждой точке, а значит, вероятность нахождения точки на грани, а также ориентацию границы. На практике, вычисление величины изменения яркости (вероятности принадлежности к границе) надежнее и проще в интерпретации, чем расчет направления.
Если на изображении будет присутствовать однотонная область или область с плавными переходами цветов, то в результирующем изображении подобные участки будут закрашены черным цветом. Там, где имеются перепады (резкие переходы, края), крутизна изменения яркости высока и в конечном изображении в таких местах появятся яркие светлые линии.
Математически, градиент функции двух переменных для каждой точки изображения (которой и является функция яркости) — двумерный вектор, компонентами которого являются производные яркости изображения по горизонтали и вертикали. В каждой точке изображения градиентный вектор ориентирован в направлении наибольшего увеличения яркости, а его длина соответствует величине изменения яркости.
Одним из способов нахождения границ на изображении является реализация фильтра или оператора Собеля (Sobel), который позволяет найти неточное приближение градиента яркости изображения.
Строго говоря, оператор использует ядра 3×3, с которыми сворачивают исходное изображение для вычисления приближенных значений производных по горизонтали и по вертикали. Формально оператор Собеля определяется следующим образом:
Пусть A исходное изображение, а Gx и Gy - два изображения, где каждая точка содержит приближенные производные по x и по y. Они вычисляются следующим образом:
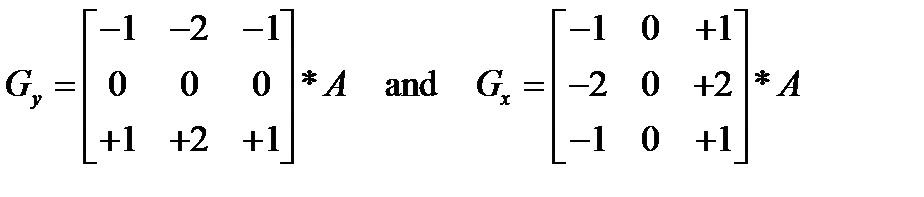
где * обозначает двухмерную операцию свертки (операцию линейной фильтрации, рассмотренную ранее).
Координата x здесь возрастает «направо», а y — «вниз». В каждой точке изображения приближенное значение величины градиента можно вычислить, используя полученные приближенные значения производных:
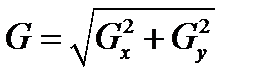
Используя эту информацию, мы также можем вычислить направление градиента:
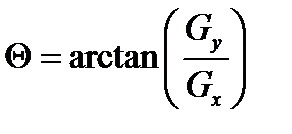
где, к примеру, угол Θ равен нулю для вертикальной границы, у которой тёмная сторона слева.
Операции свертки Gx и Gy можно использовать отдельно для нахождения вертикальных и горизонтальных границ. На рис. 4.21 приведен пример применения свертки Gx (рис. 4.21, б) и Gy (рис. 4.21, в) к исходному изображению (рис. 4.21, а). В случае совместного использования двух операций свертки Gx и Gy можем получить результат представленный на рис. 4.22.
 а) а) |  б) б) |  в) в) |
Рис. 4.21. Пример нахождения вертикальных и горизонтальных границ
В отличии от сглаживающих и контрастоповышающих фильтров, не меняющих среднюю интенсивность изображения (сумма элементов ядра равна единице), в результате применения разностных операторов получается, как правило, изображение со средним значением пикселя близким к нулю (сумма элементов ядра равна нулю). При этом пиксели со значениями близкими к нулю можно отображать белым цветом. Пиксели значения яркости, которых получились большего некоего порога, можно отображать черным цветом.
Заметим, что выделение всех пикселей, значения которых по модулю больше некоторого порога, является некоторой нелинейной локальной операцией, которую можно рассматривать как простейший пример нелинейной фильтрации.

Рис. 4.22. Пример использования оператора Собеля
Кроме фильтра Собеля можно использовать оператор Прюита (Prewitt) или оператор Щарра (Scharr), подобные алгоритму оператора Собеля, за исключением использования других матриц.
У алгоритмов нахождения границ существует несколько недостатков. Главный из них - неопределенность в выборе величины порога. Для разных частей изображения приемлемый результат обычно получается при существенно разных пороговых значениях. Кроме того, разностные фильтры очень чувствительны к шумам изображения.
Нелинейные фильтры
Основное отличие нелинейного фильтра от линейного заключается в том, что выход нелинейного фильтра формируется нелинейным образом от данных исходного изображения.
Линейные фильтры, несмотря на разнообразие производимых ими эффектов, не позволяют проделывать некоторые самые естественные операции. Хорошим примером служит пороговая фильтрация, упомянутая выше. Результатом пороговой фильтрации служит бинарное изображение, определяемое следующим образом:

Величина γ является порогом фильтрации. Пороговая фильтрация может быть использовано как предварительный этап обработки изображения перед его векторизацией.
Более сложным фильтром, нелинейным фильтром, использующим окрестность пикселя, является медиана или медианный фильтр. Здесь, так же, как и в линейных фильтрах, по пикселям передвигается окно, которое охватывает пиксели, участвующие в формировании итоговой интенсивности. Значения внутри этого окна воспринимается как одномерный массив, который сортируется в порядке возрастания. Значение, находящееся в середине отсортированного массива, поступает на выход фильтра.
Таким образом, медианная фильтрация способна эффективно справляться с импульсными помехами, когда помехи независимо воздействуют на отдельные пиксели. Примером таких помех служат "битые" и "горячие" пиксели при цифровой съемке, "снеговой" шум и т. п. Например, рис. 4.23, а. Преимущество медианной фильтрации (рис. 4.23, в) перед линейной сглаживающей фильтрацией (рис. 4.23, б) заключается в том, что интенсивность пикселя шума будет заменена интенсивностью фоновых пикселей, а не будет перераспределена на соседние пиксели как при использовании сглаживающего фильтра.
 а) а) |  б) б) |  в) в) |
Рис. 4.23. Удаление шумов фильтрами размытия и медианным фильтром
