Построение плоских фигур и геометрических тел. Способы построения овалов, заменяющих эллипсы. Особенности нанесения размеров на аксонометрические изображения
Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.
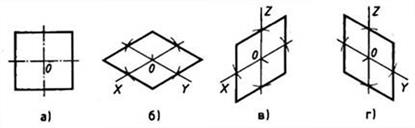
Рис. 109. Прямоугольная и изометрические проекции квадрата
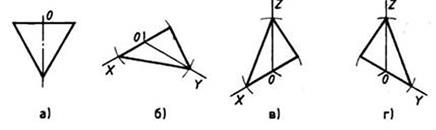
Рис. 110. Прямоугольная и изометрические проекции треугольника
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.
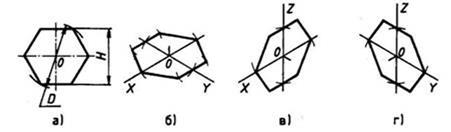
Рис. 111. Прямоугольная и изометрические проекции шестиугольника
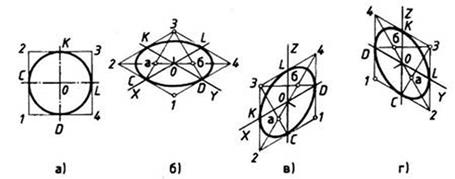
Рис. 112. Прямоугольная и изометрические проекции круга
При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.
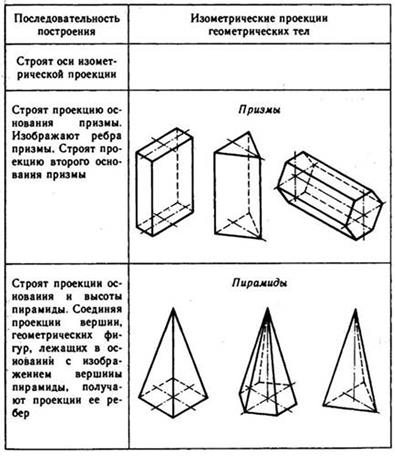
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).
10. Изометрические проекции простых геометрических тел
При выполнении прямоугольных аксонометрических проекций предметов, имеющих поверхности вращения, приходится строить проекции окружностей – эллипсы. Расположение осей эллипсов, изображение окружностей в изометрии показано на рис. 33, а, а в диметрии – на рис. 33, б, здесь же даны величины больших осей (БО) и малых осей (МО) по сравнению с натуральным диаметром (D) изображаемой окружности. На каждой оси приведены показатели искажения.
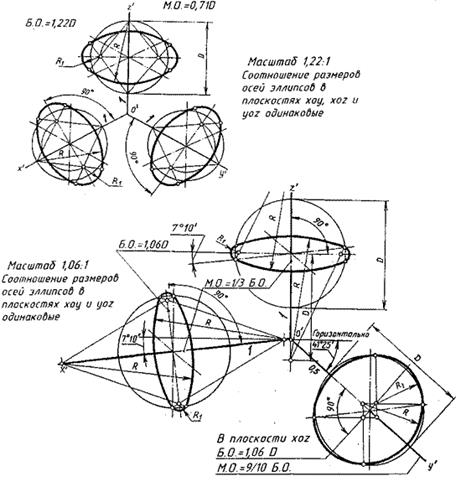
Рис. 33. Изображение окружностей: а – в изометрии; б – в диметрии
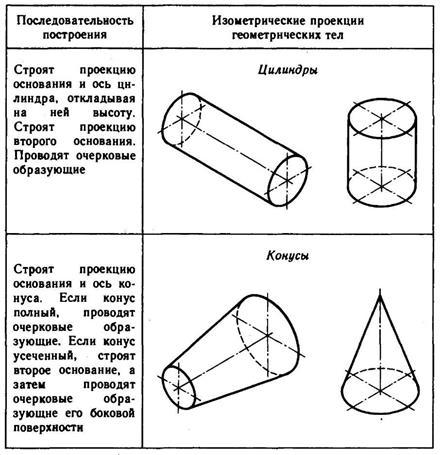
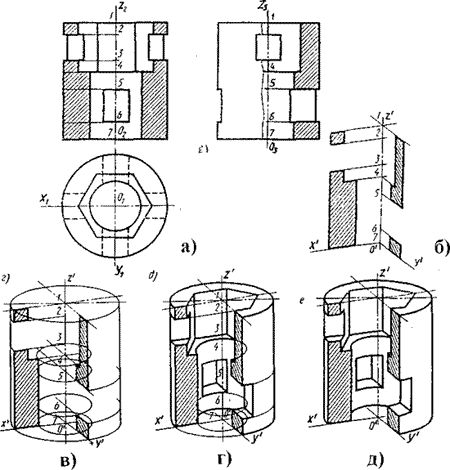
Рис. 36. Построение диметрии предмета:
а – комплексный чертёж предмета; б, в, г – стадии построения диметрии; д – диметрия предмета
10. Технический рисунок. Общие понятия и определения. Приемы построения аксонометрических осей, плоских фигур, многогранников и тел вращения средствами технического рисунка.
Техническим рисунком называют наглядное изображение, обладающее основными свойствами аксонометрических проекций или перспективного рисунка, выполненное без применения чертежных инструментов, в глазомерном масштабе, с соблюдением пропорций и возможным оттенением формы.
Рис. 124. Технические рисунки деталей, выполненных из металла (а), камня (б), стекла (в), древесины (г)
На рис. 297, а приведен технический рисунок прямоугольного треугольника, расположенного в горизонтальной плоскости проекций и выполненный в прямоугольной изомерии, а на рис. 297, б — технический рисунок прямоугольного треугольника, расположенного во фронтальной плоскости проекций и выполненного в прямоугольной диметрии.
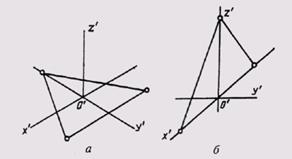
Рис. 297
На рис. 298, а показан технический рисунок шестиугольника, расположенного в горизонтальной плоскости проекций и выполненного в прямоугольной изометрии. На рис. 298, б приведен технический рисунок того же шестигранника, выполненный в прямоугольной диметрии.
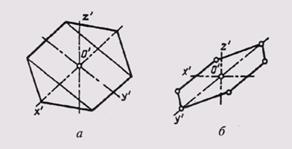
Рис. 298
Точно так же выполнен рисунок окружности, расположенной в
горизонтальной плоскости проекций (рис. 299, а), и технический рисунок такой же окружности, расположенной во фронтальной плоскости проекций и выполненный с применением правил прямоугольной ди-метрии (рис. 299, б).
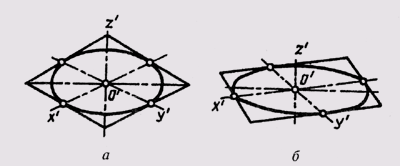
Рис. 299
Используя правила построения аксонометрических проекций и технических рисунков простейших плоских фигур, можно приступить к выполнению технических рисунков объемных геометрических фигур.
На рис. 300, а приведен технический рисунок прямой четырехгранной пирамиды, выполненный в прямоугольной изомерии, на рис. 300, б — технический рисунок прямой четырехгранной пирамиды, выполненный в прямоугольной диметрии.
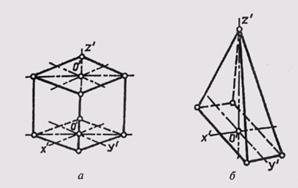
Рис. 300
Выполнение технических рисунков поверхностей вращения связано с построением эллипсов. На рис. 301, а приведен технический рисунок прямого кругового цилиндра, выполненный в прямоугольной изомерии, а на рис. 301, б — рисунок прямого кругового конуса, выполненный в прямоугольной диметрии.
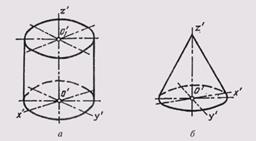
Рис. 301
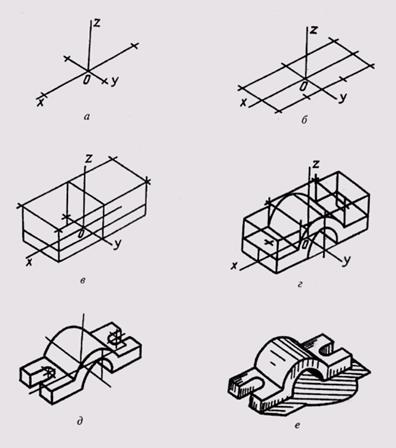
Рис. 302
Построение аксонометрических осей координат. Аксонометрические оси х' и у' для изометрической проекций наклонены по отношению к горизонтальной линии на углы в 30 и 45° и не требуют объяснений для их построения.
Построение аксонометрической оси х для диметрической проекции, наклоненной на угол 7°10', и оси у', наклоненной на угол 41° 25', рекомендуется выполнять в такой последовательности:
а) намечают точку О' - начало координат; проводят аксонометрическую ось z (вертикально); приняв за центр точку О', проводят слева дугу произвольного радиуса R, получают точку А (фиг.273,а).
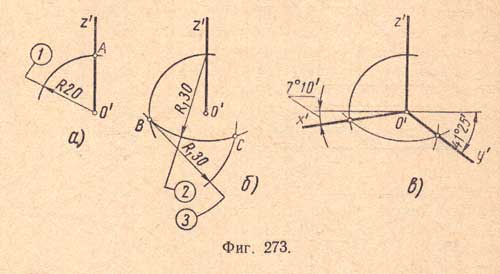
б) приняв за центр точку А, проводят дугу R1 - 1,5R, получают точку В; приняв за центр точку В, проводят дугу тем же радиусом R1 и получают точку С (фиг.273,б);
в) из точки О' проводят лучи через точки В и С (фиг.273,в). Эти лучи явятся аксонометрическими осями х' (7° 10') и у' (41° 25').
2. Построение аксонометрической проекции точки. Даны ортогональные проекции A1, A2, А3 точки А (фиг.274,a) (координаты х =20, у = 30, z = 40).
Для построения изометрической проекции точки А:
1) проводят аксонометрические оси координат х', у' и z'; откладывают по аксонометрической оси х' абсциссу (20) точки А; затем из полученной точки А'х проводят луч параллельно аксонометрической оси у' и на нем откладывают ординату (30) точки А; точка А1 явится вторичной горизонтальной проекцией точки А1 (фиг.274,а); вторичными проекциями называют аксонометрические проекции проекций геометрических элементов на координатные плоскости.
Изображение кругов в изометрических и диметрических проекциях
Из геометрии известно, что круг можно рассматривать как правильный многоугольник с большим количеством сторон. Следовательно, изометрическое изображение круга можно строить так же, описывая вокруг него квадрат (рис. 155, а). Точки касания А, В, С и D будут находиться на средине сторон квадрата и легко могут быть нанесены на аксонометрическое изображение (рис. 155, б). Промежуточные точки Е', F' и другие находим с помощью их координат. Изометрической проекцией круга является эллипс; его большая ось EG расположена под углом 60° к горизонту по большой диагонали ромба, а малая ось — под углом 30° по малой диагонали ромба.
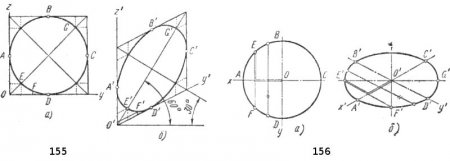
Аксонометрические изображения круга чаще строят, проводя оси х и у через центр окружности (рис. 156, а); при этом отпадает надобность в построениях квадрата и ромба. Выбрав точку О', проводим через нее оси х' и у' (рис. 156, б), откладываем на осях величины, равные радиусу окружности, получаем точки А', В', С и D'. Другие точки находим с помощью их координат; построение точки Е показано двойными тонкими линиями. Два координатных отрезка для точки Е составляют так называемую координатную ломаную, которая будет в дальнейшем широко применяться при построении точек, расположенных в пространстве. Большая ось эллипса E'G' для круга, лежащего в плоскости х'О'у', расположена горизонтально, а малая ось — вертикально.
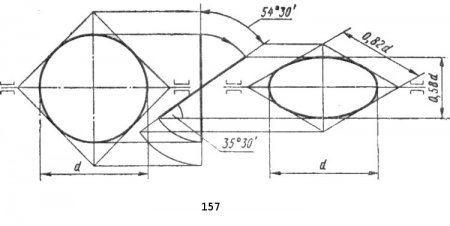
Из геометрического черчения известно (см. рис. 47), что по осям эллипса можно построить его кривую. Практически эллипс в изометрии обычно заменяют овалом, который строят следующим образом (рис. 158, б). На большой А'В' и малой CD' осях строим две окружности; они пересекают продолжение малой оси в точках 1 и 2, а большую ось — в точках 3 и 4; эти точки являются центрами для дуг овала; используя их, вычерчиваем овал с радиусами r = О'В'—О'С и R = CD' + г. Точку сопряжения дуг радиусов R и г находим, соединяя точки 1 и 4 прямой и продолжая эту прямую до пересечения с дугами в точке 5.
В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу и лишь расположены различно. В отличие от этого в прямоугольной диметрии имеются две различные формы эллипса: одна для плоскости х'О'z', а другая — для плоскостей х'О'у' и z'O'y'.
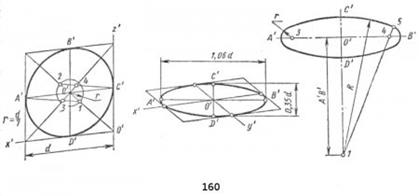
Пусть требуется построить прямоугольную диметрию окружности, лежащей в плоскости хОz (рис. 159, а). Описываем вокруг окружности квадрат и проводим его диагонали. Отмечаем точки пересечения диагоналей с окружностью и координатные отрезки, нужные для построения точек Е, F и др. Строим квадрат в прямоугольной диметрии (рис. 159, б), проводим его средние линии А'С и B'D' и диагонали. Пользуясь координатными отрезками (помечены на чертежах тонкими двойными линиями), находим точки Е', F', G' и H'. Большая ось эллипса F'G' в прямоугольной диметрии будет равна l,06d, малая ось Е'Н' будет равна 0,95d (отношение 9 : 10). Полученные восемь точек соединяем от руки, а затем обводим по лекалу. Если требуется более точное построение, то находят с помощью координатных ломаных еще ряд промежуточных точек.
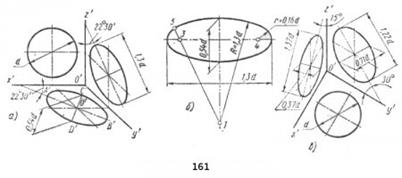
В практике эллипс нередко заменяют овалом (рис. 160, а). Центры дуг для построения овала находим так: строим ромб, его средние линии и диагонали, Из центра О' радиусом r=d/7 проводим вспомогательную окружность.
Она пересекает малую диагональ ромба в точках 1 и 2; используем эти центры для проведения дуг А'В' и CD'. Соединяем точки А' и I, С и 2; эти линии пересекают большую диагональ в точках 3 и 4. Пользуясь этими центрами, проводим дуги A'D' и В'С. При этом способе также не требуется откладывать размеры большой и малой осей; они получаются сами собой при проведении дуг.
