Геом задача повышенной сложности
Треугольники
Четырехугольники
Окружности
Комбинации
Треугольники
Задание 26 № 78
1.Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Решение.
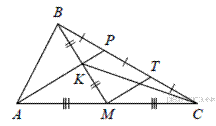 Проведём отрезок MT, параллельный AP. Тогда MT — средняя линия треугольника APC и CT = TP, а KP — средняя линия треугольника BMT и TP = BP. Обозначим площадь треугольника BKP через
Проведём отрезок MT, параллельный AP. Тогда MT — средняя линия треугольника APC и CT = TP, а KP — средняя линия треугольника BMT и TP = BP. Обозначим площадь треугольника BKP через 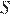 . Тогда площадь треугольника KPС, имеющего ту же высоту и вдвое больше основание, равна
. Тогда площадь треугольника KPС, имеющего ту же высоту и вдвое больше основание, равна 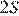 . Значит площадь треугольника CKB равна
. Значит площадь треугольника CKB равна 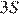 и равна площади треугольника СMK (треугольники имеют одну высоту, проведённую из вершины С, и равные равные основания), которая в свою очередь равна площади треугольника AMK. Площадь треугольника АВК равна площади треугольника АМК. Итак,
и равна площади треугольника СMK (треугольники имеют одну высоту, проведённую из вершины С, и равные равные основания), которая в свою очередь равна площади треугольника AMK. Площадь треугольника АВК равна площади треугольника АМК. Итак, 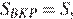
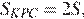
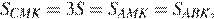
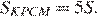 Значит,
Значит, 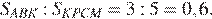
Ответ: 0,6.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1301.
Задание 26 № 311242
2.Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, при этом BD:CD=1:3. Найдите площадь четырехугольника EDCK.
Решение.
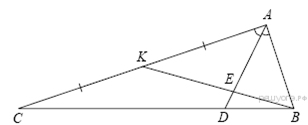
Пусть AK=KC=3x, тогда AB=2x, так как 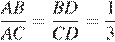 по свойству биссектрисы. Значит,
по свойству биссектрисы. Значит, 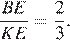
Пусть S - площадь треугольника ABC, тогда
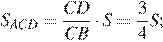
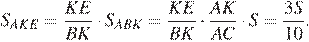
Таким образом, 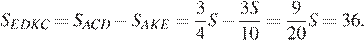
Ответ: 36.
Критерии проверки:
Задание 26 № 340325
3.В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 4 : 1. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Решение.
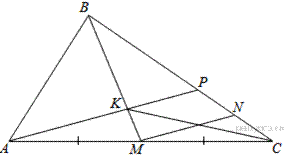
Пусть площадь треугольника  равна
равна 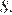 Медиана делит треугольник на два равновеликих треугольника, значит,
Медиана делит треугольник на два равновеликих треугольника, значит, 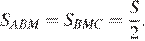 У треугольников
У треугольников 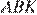 и
и 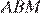 высота, проведенная к стороне
высота, проведенная к стороне 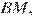 общая, поэтому площади этих треугольников относятся как их основания
общая, поэтому площади этих треугольников относятся как их основания 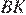 и
и 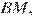 откуда:
откуда:
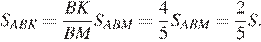
Проведём прямую 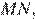 параллельную
параллельную 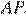 Точка
Точка 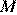 — середина
— середина 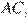 следовательно,
следовательно, 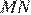 — средняя линия треугольника
— средняя линия треугольника 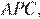 значит,
значит, 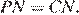 По теореме Фалеса для угла
По теореме Фалеса для угла 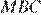 находим:
находим: 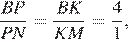 а так как
а так как  получаем, что
получаем, что 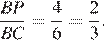
Стороны треугольников 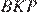 и
и 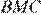 сонаправлены, их площади относятся как произведение отношений сонаправленных сторон, поэтому
сонаправлены, их площади относятся как произведение отношений сонаправленных сторон, поэтому
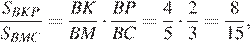
то есть 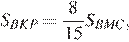 откуда
откуда 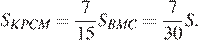
Тем самым, для искомого отношения площадей имеем:
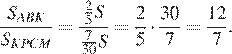
Ответ: 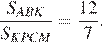
Критерии проверки:
Задание 26 № 314829
4. 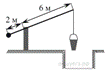
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Решение.
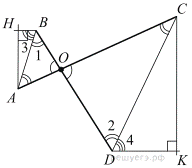
Введём обозначения как показано на рисунке. Здесь AC — положение «журавля» до опускания, BD — положение после опускания, AH — высота, на которую поднялся конец короткого плеча, CK — высота, на которую опустился конец длинного.
В равнобедренных треугольниках AOB и COD углы AOB и COD, противолежащие основаниям, равны как вертикальные, поэтому равны и углы при их основаниях. Тем самым, эти треугольники подобны по двум углам, и
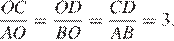
Накрест лежащие углы 1 и 2, образованные при пересечении секущей BD прямых AB и CD, равны, поэтому прямые AB и CD параллельны. Тогда стороны углов 3 и 4 попарно параллельны, а значит, эти углы равны.
Следовательно, прямоугольные треугольники AHB и CDK подобны, поскольку имеют равные острые углы. Имеем:
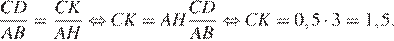
Ответ: 1,5.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 26 № 314841
5.Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Решение.
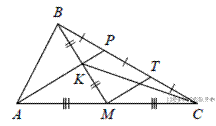 Проведём отрезок
Проведём отрезок 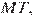 параллельный
параллельный 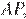 вспомним, что точка
вспомним, что точка 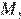 — середина
— середина 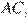 следовательно,
следовательно, 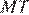 — средняя линия треугольника
— средняя линия треугольника 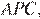 значит
значит 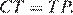 Аналогично
Аналогично 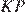 — средняя линия треугольника
— средняя линия треугольника 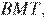 то есть
то есть 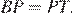
Пусть площадь треугольника 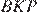 равна
равна 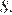 Рассмотрим треугольник
Рассмотрим треугольник 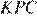 он имеет общую высоту с треугольником
он имеет общую высоту с треугольником 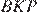 и вдвое большее основание, следовательно его площадь равна
и вдвое большее основание, следовательно его площадь равна 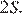 Площадь треугольника
Площадь треугольника 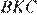 равна
равна 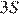 и такую же площадь имеет треугольник
и такую же площадь имеет треугольник 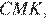 поскольку они имеют одну высоту, проведённую из вершины
поскольку они имеют одну высоту, проведённую из вершины  и равные основания. Аналогично площадь треугольника
и равные основания. Аналогично площадь треугольника 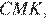 равна площади треугольника
равна площади треугольника 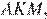 а площадь треугольника
а площадь треугольника 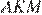 равна площади треугольника
равна площади треугольника 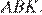
Подведём итог:
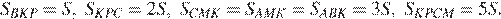
Отношение площади четырёхугольника 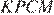 к площади четырёхугольника
к площади четырёхугольника 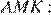
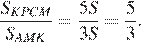
Ответ: 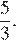
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 26 № 315070
6.Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Решение.
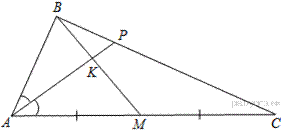
Пусть площадь треугольника  равна
равна 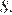 Медиана делит треугольник на два равновеликих треугольника, поэтому
Медиана делит треугольник на два равновеликих треугольника, поэтому 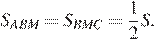 Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
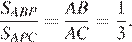
Откуда 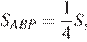
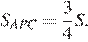 Рассмотрим треугольник
Рассмотрим треугольник 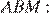
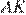 — биссектриса, следовательно:
— биссектриса, следовательно:
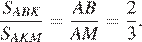
Откуда 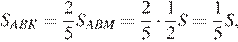
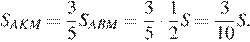 Выразим площадь треугольника
Выразим площадь треугольника 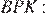
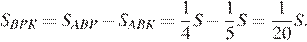
Найдём отношение площади четрёхугольника 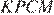 к площади треугольника
к площади треугольника 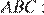
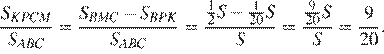
Ответ: 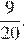
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 26 № 314866
7.Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Решение.

Пусть площадь треугольника  равна
равна 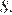 Медиана делит треугольник на два равновеликих треугольника, поэтому
Медиана делит треугольник на два равновеликих треугольника, поэтому 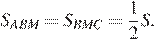 Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
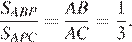
Откуда 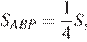
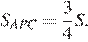 Рассмотрим треугольник
Рассмотрим треугольник 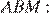
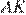 — биссектриса, следовательно:
— биссектриса, следовательно:
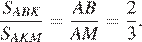
Откуда 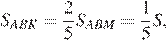
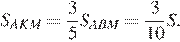 Выразим площадь треугольника
Выразим площадь треугольника 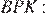
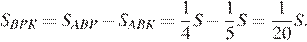
Найдём отношение площади треугольника 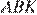 к площади четырёхугольника
к площади четырёхугольника 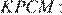
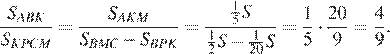
Ответ: 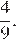
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 26 № 316361
8.Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18.
Решение.
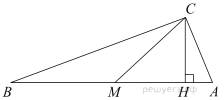
Из вершины  прямого угла прямоугольного треугольника
прямого угла прямоугольного треугольника  проведём медиану
проведём медиану 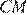 и высоту
и высоту 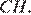 Тогда
Тогда
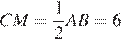
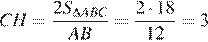
В прямоугольном треугольнике 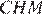 катет
катет 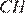 равен половине гипотенузы
равен половине гипотенузы 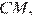 поэтому
поэтому 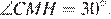
Следовательно, 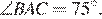
Ответ: 15°, 75° .
Критерии проверки:
Источник: МИОО: Тренировочная работа по математике 19.02.2014 вариант МА90501.
Задание 26 № 333323
9.В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC .
Решение.
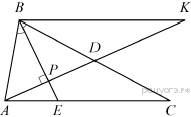 Пусть
Пусть  — точка пересечения отрезков
— точка пересечения отрезков 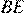 и
и 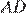 (см. рис.). Треугольник
(см. рис.). Треугольник 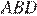 — равнобедренный, так как его биссектриса
— равнобедренный, так как его биссектриса 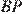 является высотой. Поэтому
является высотой. Поэтому
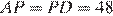 ;
; 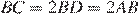 .
.
По свойству биссектрисы треугольника
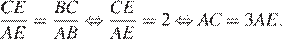
Проведём через вершину 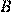 прямую, параллельную
прямую, параллельную 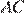 . Пусть
. Пусть 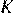 — точка пересечения этой прямой с продолжением медианы
— точка пересечения этой прямой с продолжением медианы 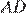 . Тогда
. Тогда 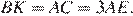
Из подобия треугольников 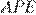 и
и 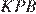 следует, что
следует, что 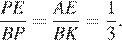 Поэтому
Поэтому  и
и 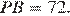 Следовательно
Следовательно
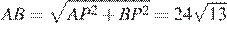 ;
; 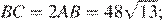
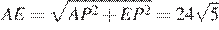 ;
; 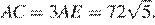
Ответ: 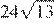 ;
;  ;
; 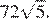
Критерии проверки:
Источник: МИОО: Тренировочная работа по математике 06.05.2014 вариант МА90701.
Задание 26 № 339514
10.Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Решение.
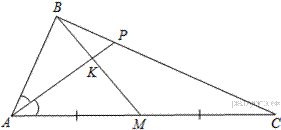
Пусть площадь треугольника  равна
равна 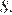 Медиана делит треугольник на два равновеликих треугольника, поэтому
Медиана делит треугольник на два равновеликих треугольника, поэтому 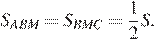 Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
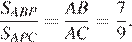
Откуда 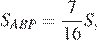
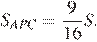 Рассмотрим треугольник
Рассмотрим треугольник 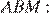
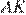 — биссектриса, следовательно:
— биссектриса, следовательно:
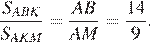
Откуда 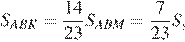
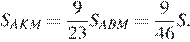 Выразим площадь треугольника
Выразим площадь треугольника 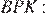
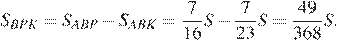
Найдём отношение площади треугольника 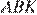 к площади четырёхугольника
к площади четырёхугольника 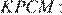
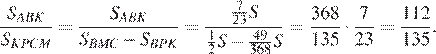
Ответ: 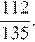
Критерии проверки:
Задание 26 № 311252
11.Стороны 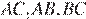 треугольника
треугольника  равны
равны 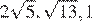 соответственно. Точка
соответственно. Точка 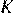 расположена вне треугольника
расположена вне треугольника 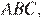 причем отрезок
причем отрезок 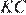 пересекает отрезок
пересекает отрезок 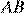 в точке, отличной от
в точке, отличной от 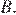 Известно, что треугольник с вершинами
Известно, что треугольник с вершинами 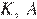 и
и  подобен исходному. Найдите косинус угла
подобен исходному. Найдите косинус угла 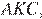 если
если 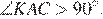
Решение.
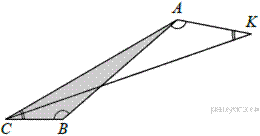
Рассмотрим подобные треугольники  и
и 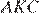 и установим соответствие между их углами.
и установим соответствие между их углами. 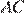 —наибольшая сторона треугольника
—наибольшая сторона треугольника 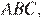 а значит,
а значит,  — наибольший угол треугольника
— наибольший угол треугольника 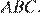 Так как в треугольнике
Так как в треугольнике 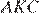 есть тупой угол
есть тупой угол 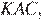 то в треугольнике
то в треугольнике  это угол
это угол 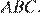 Следовательно, угол
Следовательно, угол 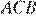 треугольника
треугольника  не равен углу
не равен углу 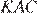 треугольника
треугольника 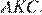 Он также не равен углу
Он также не равен углу 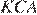 т. к. больше его (луч
т. к. больше его (луч 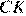 проходит между лучами
проходит между лучами 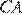 и
и 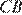 ). Следовательно,
). Следовательно, 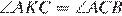 . По теореме косинусов в треугольнике
. По теореме косинусов в треугольнике  имеем:
имеем:
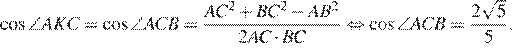
Ответ: 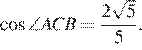
Критерии проверки:
Задание 26 № 340065
12.Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Решение.
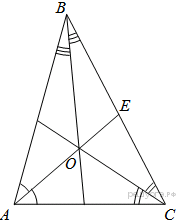 Проведем построения и введём обозначения как показано на рисунке. Рассмотрим треугольник
Проведем построения и введём обозначения как показано на рисунке. Рассмотрим треугольник 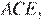
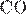 — биссектриса, по свойству биссектрисы:
— биссектриса, по свойству биссектрисы:
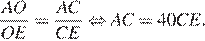
Рассмотрим треугольник 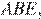
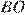 — биссектриса, по свойству биссектрисы:
— биссектриса, по свойству биссектрисы:
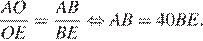
Складывая два получившихся равенства, получаем:
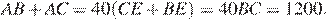
Таким образом, периметр треугольника  равен 1230.
равен 1230.
Ответ: 1230.
Критерии проверки:
Задание 26 № 351296
13.Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 28, а площадь равна 98.
Решение.

Из вершины  прямого угла прямоугольного треугольника
прямого угла прямоугольного треугольника  проведём медиану
проведём медиану 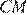 и высоту
и высоту 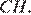 Тогда
Тогда
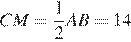
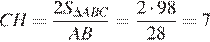
В прямоугольном треугольнике 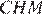 катет
катет 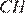 равен половине гипотенузы
равен половине гипотенузы 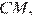 поэтому
поэтому 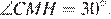
Следовательно, 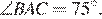
Ответ: 15°, 75° .
Задание 26 № 352418
14.В треугольнике  на его медиане
на его медиане 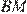 отмечена точка
отмечена точка 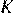 так, что
так, что 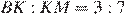 . Найдите отношение площади треугольника
. Найдите отношение площади треугольника 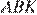 к площади треугольника
к площади треугольника 
Решение.
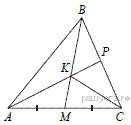 По свойству медианы, медиана
По свойству медианы, медиана 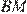 делит треугольник
делит треугольник  на два равновеликих, т.е.
на два равновеликих, т.е. 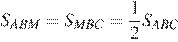 . Из условия известно, что
. Из условия известно, что 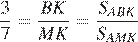 . Следовательно,
. Следовательно, 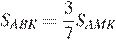
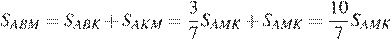
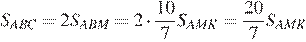
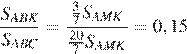
Ответ: 0,15
Задание 26 № 353377
15.Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:2, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 16.
Решение.
 Проведем построения и введём обозначения как показано на рисунке. Рассмотрим треугольник
Проведем построения и введём обозначения как показано на рисунке. Рассмотрим треугольник 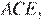
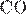 — биссектриса, по свойству биссектрисы:
— биссектриса, по свойству биссектрисы:
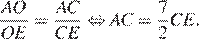
Рассмотрим треугольник 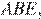
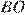 — биссектриса, по свойству биссектрисы:
— биссектриса, по свойству биссектрисы:
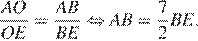
Складывая два получившихся равенства, получаем:
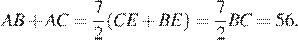
Таким образом, периметр треугольника  равен 72.
равен 72.
Ответ: 72.
Ответ: 72
Задание 26 № 353380
16.В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника ABC.
Четырёхугольники
Задание 26 № 339388
1.Высота AH ромба ABCD делит сторону CD на отрезки DH = 21 и CH = 8. Найдите высоту ромба.
Решение.
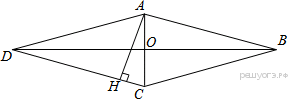 Введём обозначения как показано на рисунке. Угол
Введём обозначения как показано на рисунке. Угол 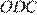 и
и 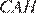 равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники
равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники 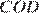 и
и  они прямоугольные, углы
они прямоугольные, углы 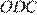 и
и 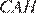 равны, следовательно, эти треугольники подобны, откуда
равны, следовательно, эти треугольники подобны, откуда 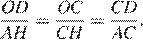 Диагонали ромба делятся точкой пересечения пополам:
Диагонали ромба делятся точкой пересечения пополам: 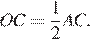 Получаем:
Получаем:
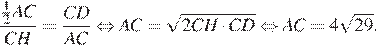
Из прямоугольного треугольника  используя теорему Пифагора найдём
используя теорему Пифагора найдём 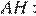
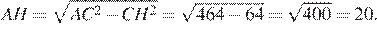
Ответ: 20.
-----------
Приведем другое решение:
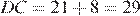
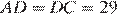
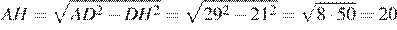
Критерии проверки:
Задание 26 № 339373
2.Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.
Решение.
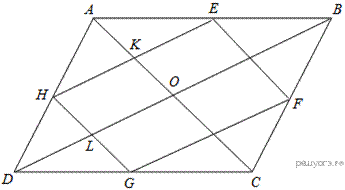 Введём обозначения как показано на рисунке. Поскольку
Введём обозначения как показано на рисунке. Поскольку 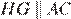 и
и 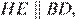 получаем, что
получаем, что 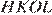 — параллелолограмм, следовательно, углы
— параллелолограмм, следовательно, углы 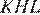 и
и 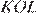 равны. Рассмотрим треугольники
равны. Рассмотрим треугольники  и
и 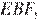 угол
угол 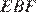 — общий, углы
— общий, углы 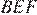 и
и 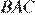 равны как соответственные при параллельных прямых, углы
равны как соответственные при параллельных прямых, углы 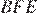 и
и 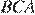 — аналогично, следовательно, треугольники
— аналогично, следовательно, треугольники  и
и 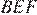 подобны по двум углам. Откуда
подобны по двум углам. Откуда 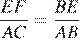 Аналогично подобны треугольники
Аналогично подобны треугольники 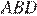 и
и 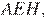 откуда
откуда 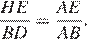 Пусть сторона ромба равна
Пусть сторона ромба равна 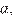 а длина короткой диагонали равна
а длина короткой диагонали равна 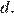 Сложим два полученных уравнения:
Сложим два полученных уравнения:
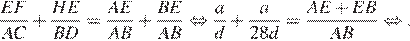
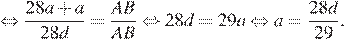
Площадь ромба можно найти как произведение сторон на синус угла между ними: 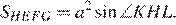 Площадь параллелограмма можно найти как половину произведения диагоналей на синус угла между ними:
Площадь параллелограмма можно найти как половину произведения диагоналей на синус угла между ними: 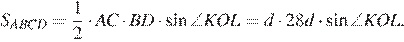 Найдём отношение площадей ромба и параллелограмма:
Найдём отношение площадей ромба и параллелограмма:
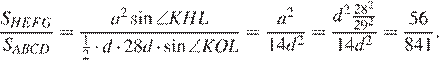
Ответ: 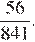
Критерии проверки:
Задание 26 № 339398
3.Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение.
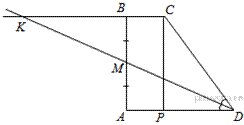 Введём обозначения как показано на рисунке. Продолжим биссектрису до пересечения с прямой
Введём обозначения как показано на рисунке. Продолжим биссектрису до пересечения с прямой 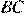 в точке
в точке 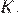 Углы
Углы 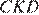 и
и 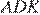 равны как накрест лежащие при параллельных прямых. Значит,
равны как накрест лежащие при параллельных прямых. Значит, 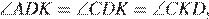 следовательно, треугольник
следовательно, треугольник 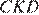 — равнобедренный:
— равнобедренный: 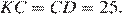 Найдём
Найдём 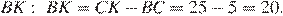 Углы
Углы 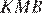 и
и 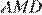 равны как вертикальные. Рассмотрим треугольники
равны как вертикальные. Рассмотрим треугольники 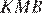 и
и 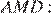 стороны
стороны 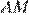 и
и 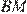 равны, углы
равны, углы 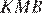 и
и 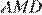 равны как вертикальные, углы
равны как вертикальные, углы 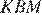 и
и  равны как накрест лежащие при параллельных прямых, следовательно, эти треугольники равны, откуда
равны как накрест лежащие при параллельных прямых, следовательно, эти треугольники равны, откуда 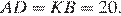 Проведём прямую
Проведём прямую 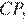 параллельную
параллельную 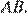 Прямая
Прямая 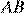 параллельна
параллельна 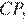 прямая
прямая 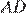 параллельна
параллельна 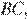 следовательно, четырёхугольник
следовательно, четырёхугольник 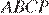 — параллелограмм, откуда
— параллелограмм, откуда 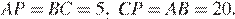 Найдём
Найдём 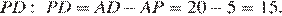 Рассмотрим треугольник
Рассмотрим треугольник 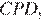 заметим, что
заметим, что
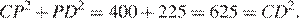
Следовательно, по теореме, обратной теореме Пифагора, получаем, что треугольник 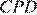 — прямоугольный, следовательно,
— прямоугольный, следовательно, 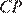 — высота трапеции. Найдём площадь трапеции:
— высота трапеции. Найдём площадь трапеции:
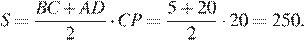
Ответ: 250.
Критерии проверки:
Задание 26 № 340359
4.Основания трапеции относятся как 1:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Решение.
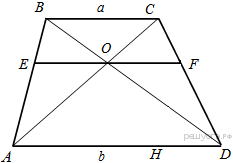 Введём обозначения как показано на рисунке. Отрезок, проходящий через точку пересечения диагоналей трапеции, равен среднему гармоническому её оснований. Пусть
Введём обозначения как показано на рисунке. Отрезок, проходящий через точку пересечения диагоналей трапеции, равен среднему гармоническому её оснований. Пусть 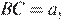 тогда
тогда 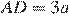 и
и 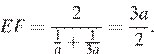 Поскольку треугольники
Поскольку треугольники 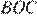 и
и 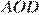 подобны, их высоты
подобны, их высоты 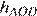 и
и 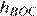 , проведенные соответственно к сторонам
, проведенные соответственно к сторонам 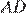 и
и 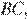 относятся как 3:1. Тем самым, для отношения искомого отношения площадей трапеций
относятся как 3:1. Тем самым, для отношения искомого отношения площадей трапеций 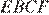 и
и  имеем:
имеем:
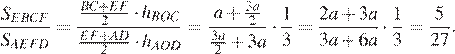
Ответ: 5:27.
Критерии проверки:
Задание 26 № 341292
5.Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Решение.
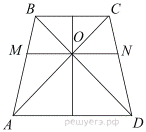
Пусть диагонали AC и BD трапеции ABCD с основаниями BC = 2a, AD = 3a пересекаются в точке O, а прямая, параллельная основаниям и проходящая через точку O, пересекает боковые стороны AB и CD в точках M и N соответственно (см. рис.).
Треугольник BOC подобен треугольнику DOA с коэффициентом 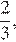 поэтому треугольник AMO подобен треугольнику ABC с коэффициентом
поэтому треугольник AMO подобен треугольнику ABC с коэффициентом 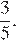 Значит,
Значит, 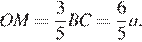 Аналогично,
Аналогично, 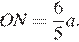 Следовательно,
Следовательно, 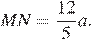 Пусть h1 и h2 — высоты подобных треугольников BOC и DOA, проведённые из общей вершины O. Тогда
Пусть h1 и h2 — высоты подобных треугольников BOC и DOA, проведённые из общей вершины O. Тогда 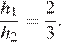 Следовательно,
Следовательно,
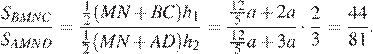
Ответ: 44:81.
Критерии проверки:
Задание 26 № 311926
6.В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.
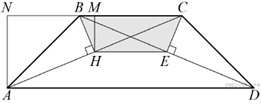
По свойству равнобедренной трапеции 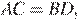 следовательно, треугольники
следовательно, треугольники  и
и 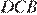 равны. Так как
равны. Так как 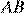 =
= 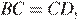 треугольники
треугольники  и
и 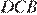 равнобедренные, следовательно,
равнобедренные, следовательно, 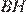 и
и 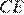 — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит, 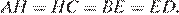 Отрезок
Отрезок 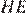 соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно, 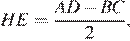 и прямые
и прямые 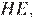
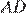 и
и 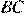 параллельны, поэтому,
параллельны, поэтому, 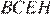 — трапеция. Проведём
— трапеция. Проведём 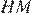 — высоту трапеции
— высоту трапеции 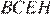 и
и 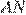 — высоту трапеции
— высоту трапеции
