Пространственные кривые линии. Винтовые линии

Цилиндрическая винтовая линия – это пространственная кривая, получающаяся в результате двойного равномерного движения точки – вращения вокруг оси и поступательного движения вдоль прямой, параллельной этой оси.

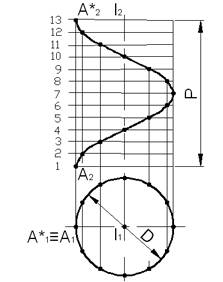
Шаг винтовой линии – расстояние между двумя её соседними витками в направлении, параллельном оси винтовой линии.

На плоскость проекций, параллельную оси вращения, винтовая линия проецируется в синусоиду.

Разверткой цилиндрической винтовойлинии является прямая линия.

Если ось вращения будет перпендикулярна к одной из плоскостей проекций, то на эту плоскость винтовая линия будет проецироваться в окружность.

Правая винтовая линия образована вращением точки по часовой стрелке, если смотреть в направлении удаления точки.

Левая винтовая линия образована вращением точки против часовой стрелки, если смотреть в направлении удаления точки.

Коническая винтовая линия – это пространственная кривая, получающаяся в результате двойного равномерного движения точки – вращения вокруг оси и поступательного движения вдоль прямой, пересекающейся с этой осью.

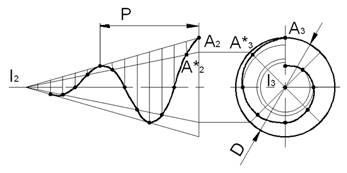
Проекция конической винтовой линии на плоскости, параллельную оси конуса (в данном случае фронтальная проекция), представляет собой синусоиду с уменьшающейся высотой волны.

Проекция на плоскости, перпендикулярной к оси конуса, представляет собой спираль Архимеда

Поверхности вращения

Поверхности вращения образованы вращением образующей вокруг неподвижной оси. Каждая точка образующей описывает около оси окружность, и, следовательно, любая плоскость, перпендикулярная оси, пересечет поверхность вращения по окружности – параллели. Параллель максимального радиуса называется экватором.Плоскость, проходящая через ось поверхности вращения, пересекает поверхность по меридиану. Главный меридианполучается при проведении через ось фронтальной плоскости уровня. Точка, принадлежащая поверхности, расположена на некоторой линии, принадлежащей поверхности, например, параллели или образующей.

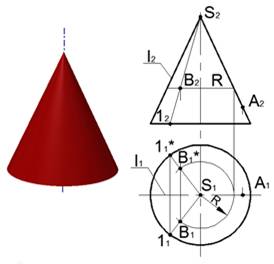
Конусобразуется вращением прямой m, проходящей через точку S на оси I

На чертеже по заданным проекциям A1 и B2 точек, принадлежащих конической поверхности, найдены проекции A2 и B1. Построение выполнено при помощи крайней правой образующей (S−A) и образующей (S−1), проведенной через точку B. Можно построить недостающую проекцию точки B и с помощью параллели радиуса R.

Цилиндробразуется вращением прямой L, параллельной оси, вокруг этой оси I.

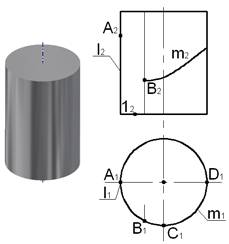
На чертеже цилиндра, ось которого перпендикулярна Π1, для построения проекций точек кривой линии m, принадлежащей поверхности цилиндра, использованы образующие цилиндра, проходящие через точки кривой.

Сфера образуется вращением окружности вокруг оси I, проходящей через центр окружности.

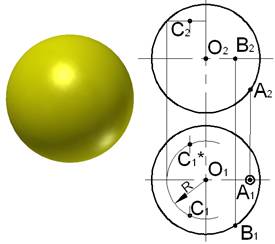
На чертеже сферы по фронтальным проекциям точек A, B, C найдены их горизонтальные проекции. Проекция точки A1 построена по условию принадлежности точки главному меридиану сферы. Точка B принадлежит экватору сферы. Для определения C1 построена горизонтальная проекция параллели, проходящей через точку C, параллель радиуса R.

Тор открытый – ось вращения расположена в плоскости окружности и не пересекает ее.

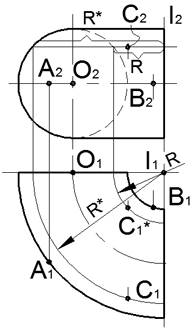
На чертеже одной четвертой части тора, ось которого перпендикулярна Π1, показано построение проекций точек, принадлежащих поверхности. Точки A и B расположены на экваторе тора. Фронтальной проекции C2 точки C соответствуют две горизонтальные проекции C1 и C∗1 на задней и передней части тора, расположенные на параллелях радиусов R и R∗.

Тор закрытый – ось вращения расположена в плоскости окружности и совпадает с ее хордой.