Вращение вокруг прямых уровня

При вращении вокруг прямых уровня геометрический объект переводят в положение, параллельное одной из плоскостей проекций, за один поворот вокруг оси, параллельной этой плоскости проекций. Каждая точка объекта при его вращении перемещается по окружности, лежащей в плоскости, перпендикулярной оси вращения.

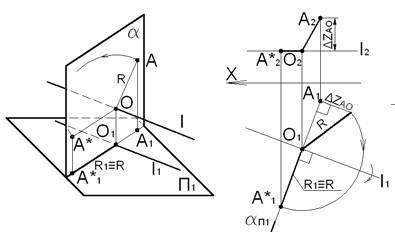
Точка A вращается в горизонтально проецирующей плоскости α, перпендикулярной оси вращения I:

A∈α,α⊥I∧I∥Π1, α⊥Π1

Горизонтальный след αΠ1 плоскости α проходит через A1 и перпендикулярен оси вращения: A∈αΠ1, αΠ1⊥I1. Центр вращения O является точкой пересечения оси вращения с плоскостью α:

O=I∩α.

Радиус вращения точки A:

AO⊥I,∣AO∣=∣R∣

Если повернуть AO до положения, параллельного плоскости Π1, то проекция R на плоскость Π1будет равна натуральной величине ∣AO∣. На основании теоремы о проекциях прямого угла горизонтальная проекция точки A может перемещаться только по перпендикуляру к горизонтальной проекции горизонтали.

A∗1O1=∣AO∣=R.

Натуральная величина радиуса вращения R равна гипотенузе вспомогательного прямоугольного треугольника, один катет которого равен горизонтальной проекции A1O1 радиуса AO, а другой – разности удалений точек A и O от плоскости Π1 – △ZA0.

A∗1 и A∗2 – новые горизонтальная и фронтальная проекции повернутой точки A.

Рассмотрим пример определения натуральной величины треугольника ABC способом вращения вокруг фронтали CK плоскости треугольника, проведенной вне треугольника.

Треугольник поворачивается вокруг оси, параллельной фронтальной плоскости проекций Π2, до положения, параллельного плоскости проекций Π2.

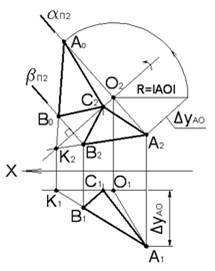
В плоскости треугольника через вершину C проводим фронталь CK. Горизонтальная проекция горизонтали C1K1 параллельна оси OX. Точка K одновременно принадлежит стороне AB.

CK∥Π2∧CK∈△ABC∧C1K1∥OX∧K2∈A2B2

Точки A и B вращаются во фронтально проецирующих плоскостях α и β, перпендикулярных оси вращения CK

α⊥CK∧β⊥CK,

αΠ1⊥C2K2∧βΠ2C2K2.

Точка C не меняет своего положения. Когда треугольник займет положение, параллельное фронтальной плоскости проекций, радиусы вращения точек A и B будут параллельны Π2 и проецируются на плоскость проекций в натуральную величину.

Центром вращения точки A является точка O=CK∩α, радиусом вращения – отрезок ∣OA∣=∣R∣. Натуральную величину ∣OA∣определяем, используя способ прямоугольного треугольника.

От центра вращения O точки A по направлению следа αΠ2 откладываем длину радиуса вращения и отмечаем новую горизонтальную проекцию AO точки A. Новую проекцию BO точки Bопределяем из условия, что точка B принадлежит прямой CK и плоскости β, в которой она вращается:

BO∈K2CO∧B∈βΠ2.

Совмещение

Если за ось вращения принять нулевую линию уровня (след плоскости), то такое вращение будет называться совмещением.

Рассмотрим плоскость общего положения α с принадлежащей ей точкой A совмещена с горизонтальной плоскостью проекций Π1 вращением вокруг горизонтального следа αΠ1.

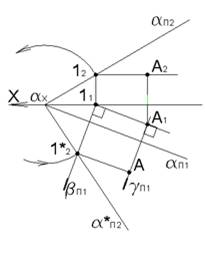
Чтобы построить совмещенное положение точки A, принадлежащей плоскости α, достаточно построить совмещенный след α∗Π2 и провести совмещенную горизонталь, которой принадлежит точка A. Для построения совмещенного следа α∗Π2 определено совмещенное положение 1∗2 точки 1∈α∗Π2. Через точку 1 проведена горизонтально проецирующая плоскость β, в которой вращается точка 1. Расстояние от точки схода следов αx до точки 12 истинное, поэтому точка 1∗2 определена на пересечении дуги из центра αx радиусом R=αx12 и горизонтального следа βΠ1плоскости β, 1∈β.

Искомая точка A определяется в пересечении совмещенной горизонтали A–1∗2и горизонтального следа γΠ1 плоскости γ, в которой вращается точка A.

Пример

В плоскости α задана точка A.Построить прямоугольный треугольник ABC, сторона которого ACсоставляет с горизонтальным следом плоскости угол 30∘. Катет ∣AC∣=35 мм, катет ∣AB∣=20 мм.

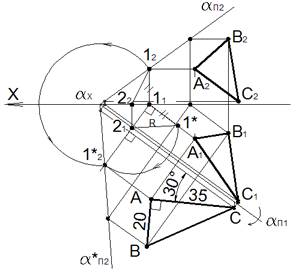
Совместим плоскость α общего положения с горизонтальной плоскостью проекций, то есть будем вращать плоскость α вокруг горизонтального следа αΠ1.

Проведем через точку A горизонталь плоскости. Выберем точку 1, лежащую на фронтальном следе, она совпадает со своей фронтальной проекцией 12(11 – горизонтальная проекция точки 1). Проведем прямую 1121 перпендикулярно оси вращения – горизонтальному следу плоскости – αΠ1. На этой прямой должна находиться точка 1 (после совмещения плоскости α с плоскостью Π1) на расстоянии, равном радиусу вращения точки 1. Длину радиуса вращения можно определить как гипотенузу прямоугольного треугольника с катетами 2111 и 111∗.

Проведя из точки схода следов αx дугу радиусом αx12 до пересечения с прямой 1121, получаем новое совмещенное с плоскостью Π1положение точки 1 (точка 1∗2). Через нее проводим совмещенный след α∗Π2.

Строим треугольник ABC в соответствии с условиями примера в натуральную величину. Чтобы построить проекции треугольника, принадлежащего плоскостиα,поступим следующим образом. Каждая точка плоскости принадлежит горизонтали или фронтали плоскости, поэтому через точки A, B и C проводим, например, горизонтали плоскости. Горизонталь плоскости, на которой расположена точка A, уже построена (A1∗2, 11A1, 12A2). Горизонтали через точки B и C строим аналогично. По линиям проекционной связи находим горизонтальные и фронтальные проекции вершин треугольника A, B и C.

Кривая линия может быть плоской или пространственной.
Все точки плоской кривой принадлежат некоторой плоскости.
Кривая, точки которой не принадлежат одной плоскости называют пространственной.