Конспект лекций по начертательной геометрии

Я.М. Стрек, Ю.А. Стрек

Конспект лекций по начертательной геометрии

Якутск 2016

Оглавление

Методы проецирования.. 3

Инвариантные свойства параллельного проецирования.. 5

Ортогональный чертеж точки.. 9

Ортогональный чертеж прямой.. 14

Длина отрезка прямой, углы его наклона к плоскостям проекций. Способ прямоугольного треугольника.. 17

Ортогональный чертеж плоскости.. 18

Плоскости общего и частного положения.. 19

Принадлежность точки и линии плоскости. Главные (особые) линии плоскости 21

Пересечение прямой линии с плоскостью... 25

Пересечение плоскостей.. 26

Прямые и плоскости, параллельные плоскости.. 29

Прямые и плоскости, перпендикулярные плоскости.. 30

Способы преобразования чертежа. Метрические задачи.. 34

Замена плоскостей проекций.. 34

Плоскопараллельное перемещение. Вращение.. 38

Вращение вокруг проецирующих прямых.. 39

Вращение вокруг прямых уровня.. 40

Совмещение.. 42

Плоские кривые линии. Кривые второго порядка.. 45

Свойства кривой линии.. 45

Способы образования кривой.. 45

Проекционные свойства плоских кривых:. 46

Проекционные свойства пространственных кривых.. 46

Алгебраические кривые второго порядка рассматривают как плоские сечения поверхности конуса.. 47

Пространственные кривые линии. Винтовые линии.. 47

Поверхности вращения.. 48

Сечение поверхностей плоскостью... 50

Пересечение прямой линии с поверхностью... 51

Обобщенные позиционные задачи.. 53

Способ вспомогательных секущих плоскостей.. 53

Способ вспомогательных концентрических сфер.. 56

Частные случаи пересечения поверхностей второго порядка.. 58

Теорема Г. Монжа.. 58

Приближенные развертки развертывающихся поверхностей.. 62

Методы проецирования

Метод проецирования применяется для изображения геометрического объекта на плоскости. Изображение получается при пересечении проецирующих лучей с плоскостью.

Центральное проецирование.

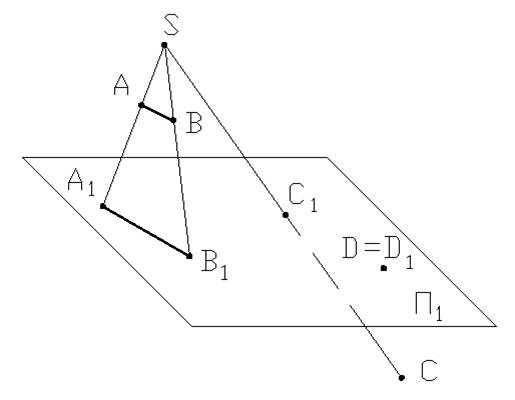
Проецирующие лучи проводятся из одной точки S – центра проекций. Π1 – плоскость проекций, точки A, B, C, D – точки пространства, D∈Π1; SA, SB – проецирующие лучи.

A1, B1, C1, D1 – центральные проекции точек A, B, C, D на плоскости проекций Π1; D1≡D.

Выводы:

1. Каждой точке пространства соответствует одна единственная проекция на плоскости Π1 при заданном S.

2. Одна проекция точки не определяет положения точки в пространстве.

Для того, чтобы определить положение точки в пространстве нужно иметь две центральные проекции точки на плоскости, полученные при двух центрах проецирования.

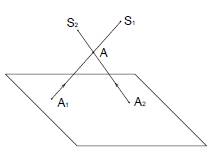
Центральные проекции дают представление только о форме предмета, геометрического объекта, а не о его размерах, A1B1>AB.

Поэтому центральные проекции применяются в архитектурно-строительных чертежах, а в машиностроительных чертежах почти не применяются.

Параллельное проецирование.

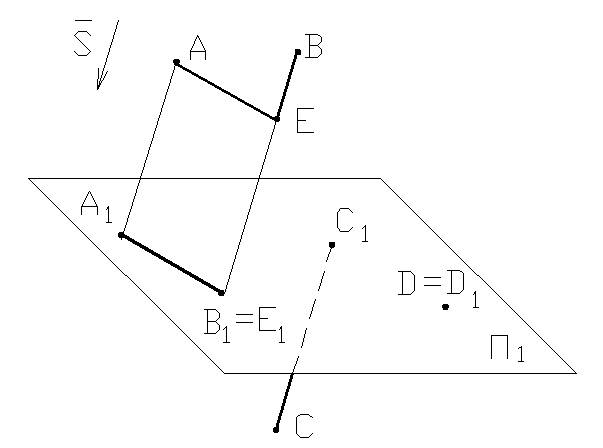
Проецирующие лучи параллельны направлению проецирования S¯. Π1 – плоскость проекций; точки A, B, C, D, E – точки пространства, D∈Π1, Точки B и E расположены на одном проецирующем луче.

A1, B1, C1, D1, E1 – параллельные проекции точек A, B, C, D на плоскости Π1; D1≡D; B1≡E1.

В зависимости от направления проецирования по отношению к плоскости проекций параллельное проецирование разделяют на косоугольное и прямоугольное (ортогональное). При ортогональном проецировании S⊥Π1

Выводы:

1. Каждой точке пространства соответствует одна единственная проекция на плоскости Π1 при заданном S.

2. Одна проекция точки не определяет положения точки в пространстве.

При ортогональном проецировании для получения двух проекций одной точки необходимо иметь две не параллельные плоскости проекций. Выберем две взаимно перпендикулярные плоскости проекций Π1⊥Π2

Инвариантные свойства параллельного проецирования

При параллельном проецировании метрические характеристики геометрических объектов нарушаются. В общем случае происходит искажение линейных и угловых величин.

Сохраняются следующие свойства:

1. Проекция точки на плоскости есть точка A→A1

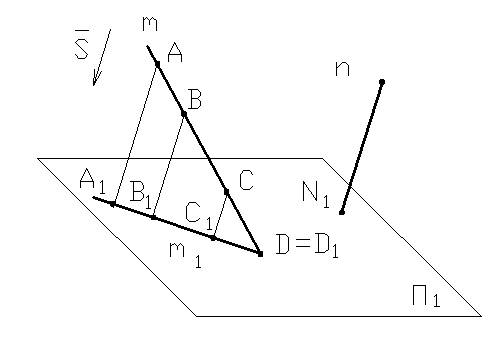
2. Проекция прямой линии на плоскости есть прямая, за исключением прямой, направление которой совпадает с направление проецирования.

m→m1, n∥S⇒n→N1

3. Если точка принадлежит прямой, то проекция точки принадлежит проекции этой прямой

A∈m⇒A1∈m1

4. Если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в том же отношении

B∈AC⇒AB:BC=A1B1:B1C1

5. Проекции отрезков параллельных прямых и их длины находятся в том же отношении, что и длины проецируемых отрезков.

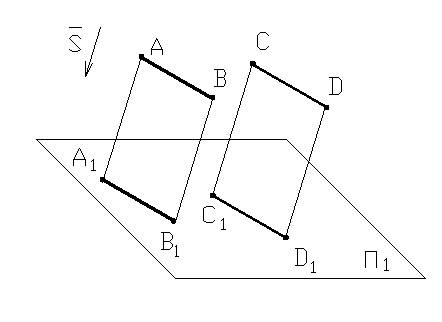
AB∥CD⇒A1B1∥C1D1∧AB:CD⇒A1B1:C1D1

6. Проекции пересекающихся прямых пересекаются. Точка пересечения проекций двух пересекающихся прямых является проекцией точки пересечения прямых.

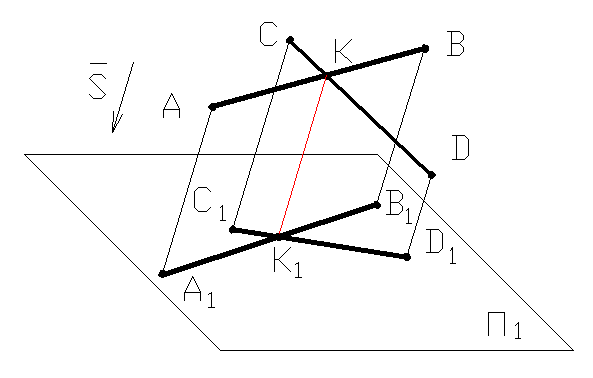
K=AB∩CD⇒K1=A1B1∩C1D1∧K1∈K

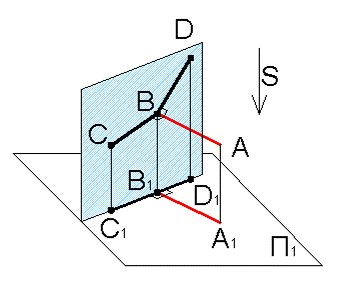
7. При ортогональномпроецировании прямой угол проецируется без искажения, если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна ей.

8. Проекции двух скрещивающихся прямых в зависимости от направления проецирования могут или пересекаться, или быть параллельными.

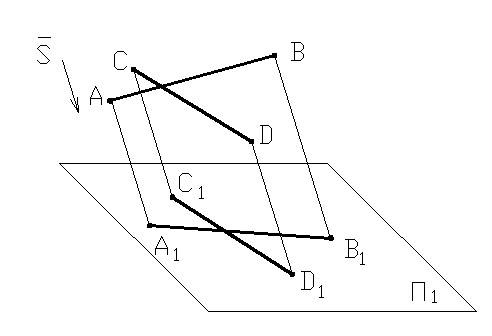
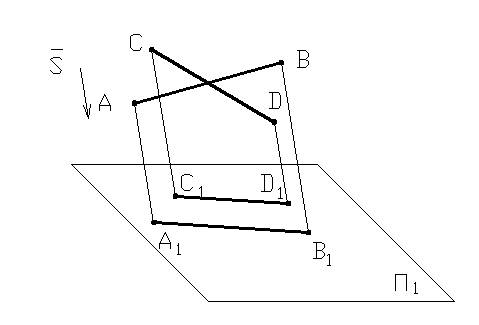
9. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость без искажения

△ABC∥Π1→△A1B1C1=|△ABC|

10. При параллельном перемещении фигуры или плоскости проекций изображение фигуры на этой плоскости не изменяется.

Ортогональный чертеж точки

Метод проецирование позволяет строить изображения по заданному оригиналу, т.е. решать прямую задачу начертательной геометрии. Однако, возникает и обратная задача, заключающаяся в восстановлении оригинала по его проекционным изображениям.

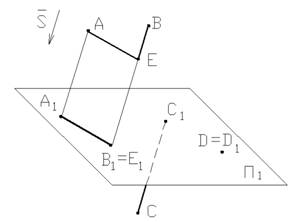
Рассмотрим точки B и E. Они расположены на одном проецирующем луче. Изображения этих точек на плоскости Π1 совпадают. По проекциям нельзя установить, какая из точек расположена ближе к плоскости Π1. Следовательно, проекционный чертеж не обладает свойством обратимости.

По схеме Гаспара Монжа геометрический объект проецируется ортогонально на две взаимно перпендикулярные плоскости проекций

Π1⊥Π2

Π1 – горизонтальная плоскость проекций;

Π2 – фронтальная плоскость проекций.

Эти плоскости делят пространство на четыре квадранта.

После проецирования оригинала плоскости Π1 и Π2 совмещаются в одну плоскость. Плоскость Π1вращается вокруг оси OX по часовой стрелке.

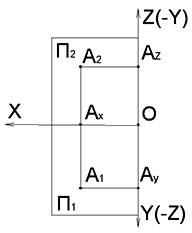
Полученный чертеж называется эпюром Монжа. Эпюр Монжа называют также комплексным чертежом.

На практике при изображении сложных геометрических форм приходится увеличивать число проекций. Введем третью плоскость проекций Π3.

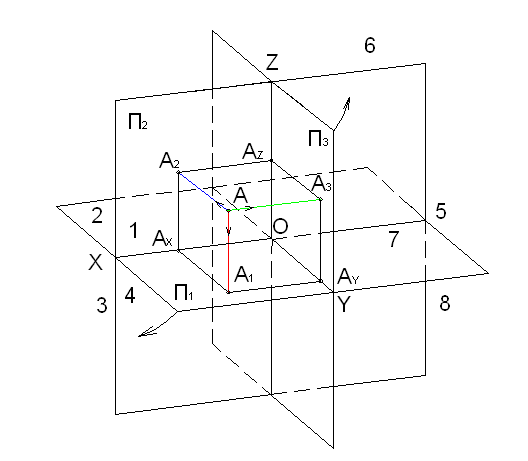
Π1 – горизонтальная плоскость проекций;

Π2 – фронтальная плоскость проекций;

Π3 – профильная плоскость проекций.

OX – ось абсцисс;

OY – ось ординат;

OZ – ось аппликат.

Точка O – начало координат.

Пространство делится тремя взаимно перпендикулярными плоскостями проекций на восемь октантов: 1, 2, 3, 4, 5, 6, 7, 8.

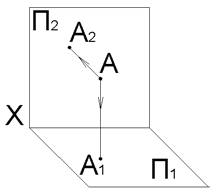
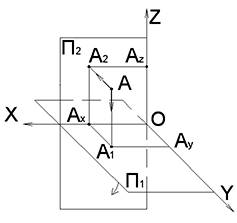
Рассмотрим точку пространства A относительно Π1⊥Π2⊥Π3.

Построим ортогональные проекции точки A, для этого опустим перпендикуляры из точки A на плоскости проекций.

A1 – горизонтальная проекция точки A,

A2 – фронтальная проекция точки A,

A3 – профильная проекция точки A.

Комплексный чертеж получается, если горизонтальную и профильную плоскости проекций совместить с фронтальной плоскостью проекций.

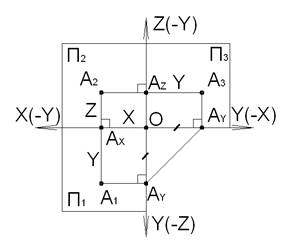
На рисунке представлен комплексный чертежточки A. Расстояния от точки до плоскостей проекций называются координатами точки – X, Y, Z – A(X,Y,Z).

X=A−A3=A2−AZ=A1−AY=O−AX – расстояние до плоскости проекций Π3;

Y=A−A2=A3−AZ=A1−AX=O−AY – расстояние до плоскости проекций Π2;

Z=A−A1=A2−AX=A3−AY=O−AZ – расстояние до плоскости проекций Π1.

На комплексном чертеже две проекции точки A1 и A2, A1 и A3, A2 и A3 расположены на одном перпендикуляре, называемом линией проекционной связи, к соответствующей оси координат. Линии проекционной связи проходят через точки Ax, Ay, Az.

(A1−A2)⊥OX, (A1−A3)⊥OY, (A2−A3)⊥OZ

1. Положение точки в пространстве однозначно определяется тремя ее координатами A(X,Y,Z).

2. Две проекции точки вполне определяют положение точки в пространстве.

3. По двум ортогональным проекциям точки можно построить ее третью проекцию.

Горизонтальная проекция точки имеет координаты X и Y, фронтальная проекция – X и Z, профильная проекция – Y и Z.

В таблице приведены знаки координат у точек, расположенных в различных квадрантах пространства.

Координаты	Квадрант
I	II	III	IV	V	VI	VII	VIII
X	+	+	+	+	−	−	−	−
Y	+	−	−	+	+	−	−	+
Z	+	+	−	−	+	+	−	−

Рассмотрим подробнее комплексные чертежи точек, расположенных в различных квадрантах пространства.

Точка A расположена в I квадранте

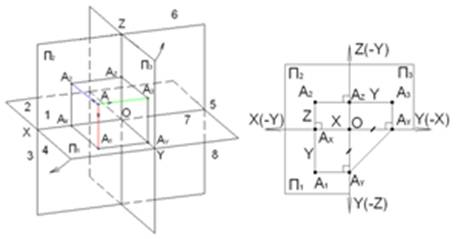
Точка A расположена в II квадранте

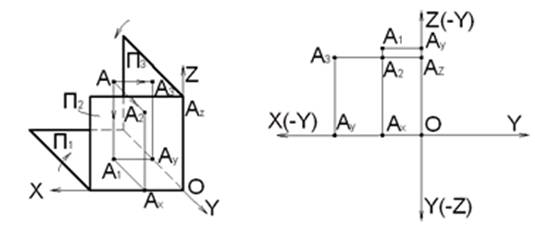
Точка A расположена в III квадранте

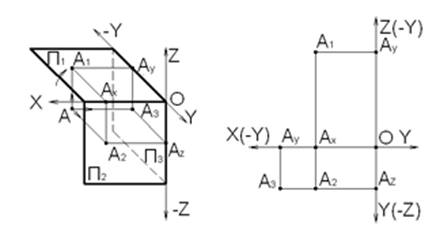
Точка A расположена в IV квадранте

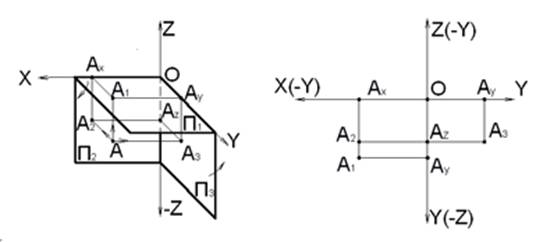
Ортогональный чертеж прямой

Прямая, не параллельная и не перпендикулярная плоскости проекций, называется прямой общего положения.

На рисунке отрезок прямой AB является прямой общего положения, точка K принадлежит отрезку в соответствии с инвариантным свойством, поскольку

K1∈A1B1∧K2∈A2B2∧K3∈A3B3

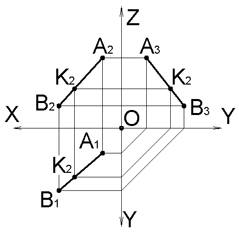
Прямой частного положения называется прямая, параллельная или перпендикулярная плоскостям проекций.

Прямые, параллельные плоскостям проекций – линии уровня.

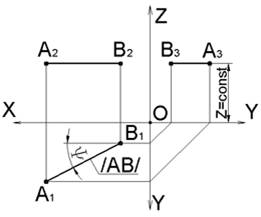
Прямая, параллельная горизонтальной плоскости проекций Π1, называется горизонталью или горизонтальной прямой, или горизонтальной линией уровня. Все точки этой прямой равноудалены от горизонтальной плоскости проекций Π1. Горизонтальная проекция A1B1 равна натуральной величине отрезка AB. Угол между A1B1 и осью OX равен натуральной величине угла между горизонталью AB и фронтальной плоскостью проекций Π2.

AB∥Π1→Z=const; A1B1=|AB|; A1B1∧OX=AB∧Π2=ψ

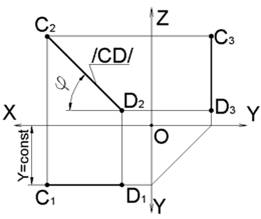
Прямая, параллельная фронтальной плоскости проекций Π2, называется фронталью.

CD∥Π2→Y=const; C2D2=|CD|; C2D2∧OX=CD∧Π1=φ

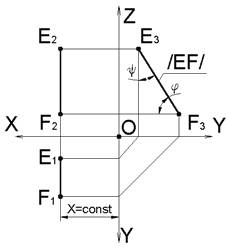
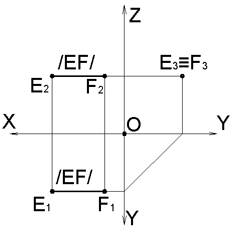
Прямая, параллельная профильной плоскости проекций Π3, называется профильной прямой.

EF∥Π3→X=const; E3F3=|EF|E3F3∧OY=EF∧Π1=φ; E3F3∧OZ=EF∧Π2=ψ

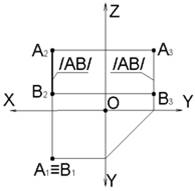
Прямая, перпендикулярная горизонтальной плоскости проекций Π1, называется горизонтально-проецирующей прямой.

AB⊥Π1→A1≡B1; A2B2=|AB|∧AB∥Π2

Прямая, перпендикулярная фронтальной плоскости проекций Π2 называется фронтально-проецирующей.

CD⊥Π2→C2≡D2; C1D1=|CD|∥Π1

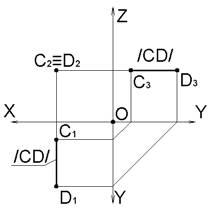
Прямая, перпендикулярная профильной плоскости проекций называется профильно-проецирующей прямой.

EF⊥Π3→E3≡F3; E1F1=E2F2=|EF|∧EF∥Π1∧EF∥Π2

Пересечение плоскостей

Две плоскости пересекаются по прямой линии, которую можно построить по двум их общим точкам.

Видимость.Линия пересечения всегда видима на плоскостях проекций, видимость прямых, расположенных в пересекающихся плоскостях, определяется по конкурирующим точкам.

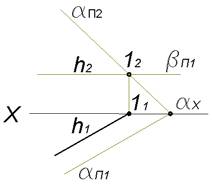
Частный случай пересечения плоскости общего положения α с горизонтальной плоскостью β. Линия пересечения плоскостей является горизонталью

α∩β∥Π1=h⇒h∥Π1

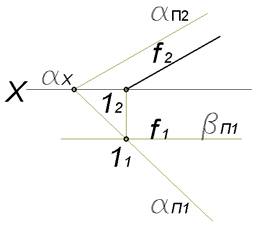
Если одна из пересекающих плоскостей параллельна фронтальной плоскости проекций Π2, то линия пересечения также параллельна фронтальной плоскости проекций:

α∩β∥Π2=f⇒f∥Π2

Рассмотрим задачу на пересечение фронтально проецирующей плоскости α и плоскости треугольника ABC общего положения. △ABC∩α⊥Π2=(1−2)−?

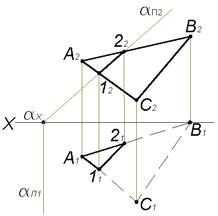
Линия пересечения двух плоскостей – это линия, принадлежащая каждой из них, следовательно, и фронтально проецирующей плоскости α. Фронтальная проекция линии пересечения плоскостей совпадает с фронтальным следом плоскости

Для построения горизонтальной проекции линии пересечения плоскостей определяем точки 11 и 21 принадлежащие сторонам AC и AB

1∈AC, 2∈AB⇒11∈A1C1, 21∈A1B1

Плоскости α и △ABC считаются непрозрачными при определении видимости, поэтому на горизонтальной проекции видимым является треугольник A11121. Фронтальная проекция треугольника A2B2C2 видима полностью.

Пример

Построить проекции линии пересечения треугольников ABC и DEF. Определить видимость треугольников относительно плоскостей проекций.

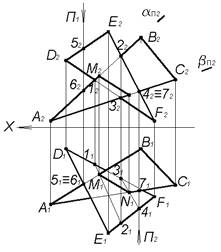
Линия пересечения треугольников M−N построена по точкам пересечения сторон AB и ACтреугольника ABC с плоскостью другого треугольника.

Для определения точки M пересечения стороны AB с △ABC необходимо:

1. через сторону AB провести фронтально проецирующую плоскость α;

2. построить линию пересечения этой плоскости с плоскостью треугольника DEF;

3. точка M находится на пересечении линии 1−2 со стороной AB треугольника ABC точка Mпринадлежит линии пересечения заданных треугольников.

Аналогично определена точка N с помощью проведения вспомогательной фронтально проецирующей плоскости β через сторону AC треугольника ABC.

Пример

Через точку A провести отрезок прямой DE, параллельный горизонтали △ABC.

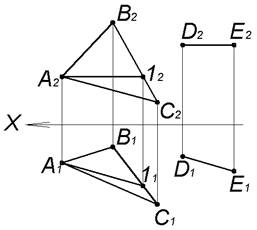
Из вершины A в плоскости треугольника ABC проведем горизонталь A−1.Фронтальная проекция отрезка D2E2 параллельна оси OX.

Горизонтальная проекция отрезка D1E1 параллельна горизонтальной проекции горизонтали A111.

Две плоскости взаимно параллельны, еслидве пересекающиеся прямые одной плоскости, параллельны двум пересекающимся прямым другойплоскости. У параллельных плоскостей одноименные главные их линии параллельны.

Пример

Через точку A провести плоскость β, параллельную плоскости α, заданной следами.

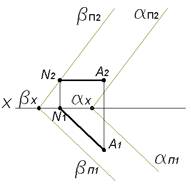
Чтобы построить плоскость, содержащую точку A и параллельную плоскости α, через точку A проведем одну из главных линий плоскости α например, горизонталь AN, параллельную плоскости α. Через фронтальный след горизонтали, точку N, проходит фронтальный след плоскости β, βΠ2∥αΠ2 Горизонтальный след βΠ2∥αΠ1 проходит через точку схода следов βX=βΠ2∩OX.

Пример

Через точку A провести плоскость α, перпендикулярную прямой m. Плоскость α задать следами.

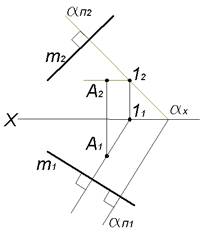
Через точку A проведем горизонталь A−1 перпендикулярно прямой

A2−12∥OX, (A1−11)⊥m1

Через фронтальный след 12 горизонтали A−1 проведем перпендикулярно прямой mфронтальный след αΠ2 плоскости. Горизонтальны след αΠ1 плоскости α проходит через точку схода следов плоскости α перпендикулярно горизонтальной проекции прямой m

αΠ1⊥m1

Пример

Восставить перпендикуляр к плоскости α в данной ее точке K.

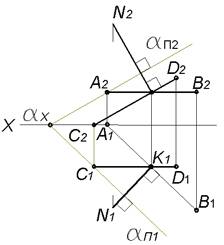
В плоскости α проведем горизонталь AB и фронталь CD. Проекции перпендикуляра к плоскости составляют прямые углы с одноименными проекциями горизонтали и фронтали плоскости α.

K1N1⊥A1B1∧K2N2⊥C2D2, K1N1⊥αΠ1∧K2N2⊥αΠ2

Прямая KN перпендикулярна любым прямым этой плоскости.

Пример

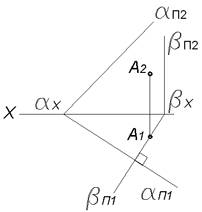
Через точку A провести горизонтально проецирующую плоскость β перпендикулярную плоскости Плоскость β задать следами.

Горизонтальный след βΠ1 плоскости проводим через горизонтальную проекцию A1 точки Aперпендикулярно горизонтальному следу αΠ1

Пример

Через точку D провести плоскость β, перпендикулярную плоскости ABC. Плоскость задать пересекающимися прямыми DE и DF.

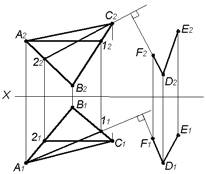
В плоскости △ABC проведем горизонталь A−1 и фронталь С−2. Отрезок DF построен перпендикулярно плоскости △ABC, поскольку D1F1⊥A111, D2F2⊥C222. Отрезок DE новой плоскости проведен произвольно.

Пример

Перпендикулярны ли плоскости, если их следы взаимно перпендикулярны?.

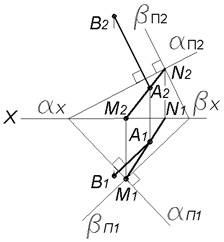
Построим линию MN пересечения плоскостей:

αΠ1∩βΠ1=M1, M2∈OX, αΠ2∩βΠ2=N2, N1∈OX.

Из точки A∈MN проведем отрезок AB так, чтобы

A1B1∥βΠ1∧A2B2∥βΠ2

Отрезок AB⊥α, поскольку A1B1⊥αΠ1∧A2B2⊥αΠ2, но он не принадлежит плоскости β.

Поэтому плоскости α и β не перпендикулярны друг другу.

Способы преобразования чертежа. Метрические задачи

Рассматривают два способа преобразования:

· способ замены плоскостей проекций.

· способ вращения.

Вращение выполняют:

· без указания осей (способ плоскопараллельного перемещения);

· вокруг проецирующих прямых;

· вокруг горизонтали или фронтали плоскости;

· вокруг следа плоскости (способ совмещения).

При решении задач способом замены плоскостей проекций положение геометрических объектов не изменяется. Изменяется положение плоскостей проекций, чтобы при новых условиях проецирования эти геометрические объекты имели бы частное положение. Направление проецирования или остается ортогональным, или изменяется.

При решении задач способом перемещения (вращения) положение плоскостей проекций и направление проецирования не изменяются. Геометрические объекты перемещаются в пространстве до принятия частного положения по отношению к данной системе плоскостей проекций.

Замена плоскостей проекций

Сущность способа заключается в следующем:

· Положение геометрического объекта не меняется по отношению к старой системе плоскостей проекций.

· Новая система взаимно перпендикулярных плоскостей проекций выбирается так, чтобы рассматриваемый геометрический объект оказался бы в частном положении по отношению к одной из плоскостей новой системы.

· Направление проецирования сохраняется ортогональным.

На рисунках показаны схемы построения новых (дополнительных) проекций точек A и B.

В системе плоскостей проекций Π2⊥Π1 заданы точки A(A1,A2) и B(B1,B2). Введены новые плоскости: Π4⊥Π)1 и Π5⊥Π2.

Пример

Найти натуральную величину треугольника ABC и угол наклона его плоскости к горизонтальной плоскости проекций Π1.

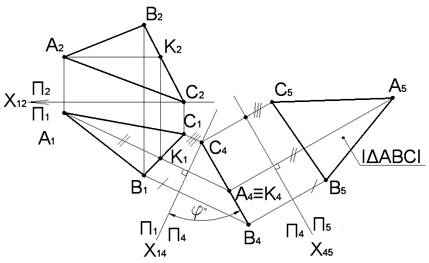
Выберем новую плоскость проекций Π4, перпендикулярную плоскости треугольника ABC, а на комплексном чертеже – перпендикулярную горизонтали AK плоскости треугольника:

Π4⊥△ABC, Π4⊥AK, AK∈△ABC, AK∥Π1

Проводим новую ось координат X14 перпендикулярно A1K1:X14⊥A1K1

Имеем систему взаимно перпендикулярных плоскостей Π1⊥Π4. Плоскость △ABC по отношению к плоскости Π4 будет проецирующей. Проводим линии проекционной связи от точек A1,B1,C1 и откладываем координаты Z вершин треугольника от новой оси X14, получаем проекции точек A4,B4,C4. Проекция треугольника ABC на Π4 – прямая C4B4, составляющая с осью X14 угол, равный натуральной величине угла между плоскостью треугольника и Π1 – угол φ.

Чтобы найти натуральную величину треугольника заменяем плоскость Π1. Вводим новую плоскость Π5, параллельную плоскости треугольника. Параллельно вырожденной проекции треугольника C4B4 проводим новую ось X45. На линиях проекционной связи отложим от новой оси отрезки, равные расстояниям от заменяемых проекций вершин A1B1C1 до заменяемой оси X14. A5B5C5=|△ABC|.

Пример

Прямую общего положения AB преобразовать во фронталь и определить ее натуральную величину и угол наклона к горизонтальной плоскости проекций Π1.

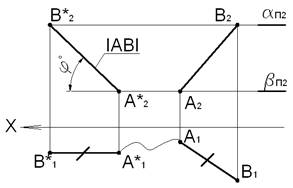
Перемещением переводим отрезок прямой AB в положение, параллельное фронтальной плоскости проекций Π2. Для этого в произвольном месте чертежа горизонтальную проекцию A1B1 отрезка AB располагаем горизонтально, параллельно оси координат OX

A∗1B∗1∥OX, A∗1B∗1=A1B1.

Точки A и B отрезка перемещаются соответственно в горизонтальных плоскостях α и β:

A∈α∧α∥Π1, B∈β∧β∥Π1.

Фронтальные проекции A2 и B2 точек A и B перемещаются по αΠ2 и βΠ2.

ZA=const, ZB=const.

Фронтальные проекции A2∗ и B2∗ перемещенных точек A∗ и B∗ находятся в проекционной связи с проекциями A∗1 и B∗1.

A∗2B∗2 – новая фронтальная проекция отрезка AB:A∗2B∗2=|AB|. Угол наклона A∗2B∗2 к оси OXявляется натуральной величиной угла наклона отрезка AB к плоскости проекций Π1:

A∗2B∗2∧OX=AB∧Π1.

Пример

Определить натуральную величину треугольника ABC и угол его наклона к плоскости проекций Π2

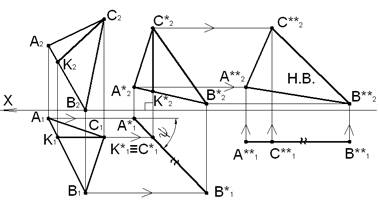
Задача решается двумя последовательными перемещениями. Первым перемещением треугольникABC приводится в положение, перпендикулярное горизонтальной плоскости проекций Π1. Вторым перемещением этот треугольник приводится в положение, параллельное фронтальной плоскости проекций Π2.

В плоскости треугольника ABC проводим фронталь CK. Перемещаем фронталь CK в положение горизонтально проецирующей прямой: CK⊥Π1. При этом плоскость треугольника станет горизонтально проецирующей плоскостью.

На чертеже проводим следующие построения. Фронтальную проекцию C2K2 располагаем перпендикулярно оси координат OX. Величина фронтальной проекции треугольника при этом не меняется. Строим фронтальную проекцию треугольника A∗2B∗2C∗2, учитывая равенство сторон треугольника: A2B2=A∗2B∗2, A2C2=A∗2C∗2, B2C2=B∗2C∗2.

Горизонтальной проекцией A1B1C1 треугольника в новом положении является отрезок прямой A∗1C∗1, угол наклона которого к оси OX является натуральной величиной угла наклона плоскости треугольника к плоскости Π2 – угол ψ. △ABC∧Π2=ψ.

Чтобы получить натуральную величину треугольника, переместим вырожденную горизонтальную проекцию треугольника (прямая A∗1C∗1,) на свободное место чертежа в положение, параллельное оси OX. Плоскость треугольника станет плоскостью уровня. Фронтальные проекции точек при этом перемещаются параллельно оси OX (сохраняется неизменной координата Z точек). На фронтальной проекции имеем натуральную величину плоскости треугольника ABC: A∗∗2B∗∗2C∗∗2=∣△ABC∣.

Совмещение

Если за ось вращения принять нулевую линию уровня (след плоскости), то такое вращение будет называться совмещением.

Рассмотрим плоскость общего положения α с принадлежащей ей точкой A совмещена с горизонтальной плоскостью проекций Π1 вращением вокруг горизонтального следа αΠ1.

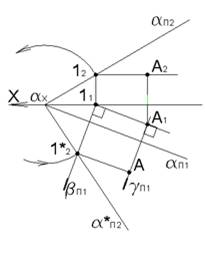
Чтобы построить совмещенное положение точки A, принадлежащей плоскости α, достаточно построить совмещенный след α∗Π2 и провести совмещенную горизонталь, которой принадлежит точка A. Для построения совмещенного следа α∗Π2 определено совмещенное положение 1∗2 точки 1∈α∗Π2. Через точку 1 проведена горизонтально проецирующая плоскость β, в которой вращается точка 1. Расстояние от точки схода следов αx до точки 12 истинное, поэтому точка 1∗2 определена на пересечении дуги из центра αx радиусом R=αx12 и горизонтального следа βΠ1плоскости β, 1∈β.

Искомая точка A определяется в пересечении совмещенной горизонтали A–1∗2и горизонтального следа γΠ1 плоскости γ, в которой вращается точка A.

Пример

В плоскости α задана точка A.Построить прямоугольный треугольник ABC, сторона которого ACсоставляет с горизонтальным следом плоскости угол 30∘. Катет ∣AC∣=35 мм, катет ∣AB∣=20 мм.

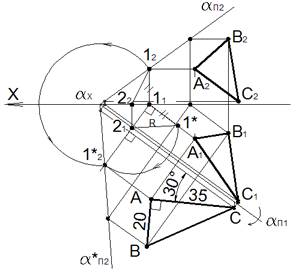
Совместим плоскость α общего положения с горизонтальной плоскостью проекций, то есть будем вращать плоскость α вокруг горизонтального следа αΠ1.

Проведем через точку A горизонталь плоскости. Выберем точку 1, лежащую на фронтальном следе, она совпадает со своей фронтальной проекцией 12(11 – горизонтальная проекция точки 1). Проведем прямую 1121 перпендикулярно оси вращения – горизонтальному следу плоскости – αΠ1. На этой прямой должна находиться точка 1 (после совмещения плоскости α с плоскостью Π1) на расстоянии, равном радиусу вращения точки 1. Длину радиуса вращения можно определить как гипотенузу прямоугольного треугольника с катетами 2111 и 111∗.

Проведя из точки схода следов αx дугу радиусом αx12 до пересечения с прямой 1121, получаем новое совмещенное с плоскостью Π1положение точки 1 (точка 1∗2). Через нее проводим совмещенный след α∗Π2.

Строим треугольник ABC в соответствии с условиями примера в натуральную величину. Чтобы построить проекции треугольника, принадлежащего плоскостиα,поступим следующим образом. Каждая точка плоскости принадлежит горизонтали или фронтали плоскости, поэтому через точки A, B и C проводим, например, горизонтали плоскости. Горизонталь плоскости, на которой расположена точка A, уже построена (A1∗2, 11A1, 12A2). Горизонтали через точки B и C строим аналогично. По линиям проекционной связи находим горизонтальные и фронтальные проекции вершин треугольника A, B и C.

Кривая линия может быть плоской или пространственной.
Все точки плоской кривой принадлежат некоторой плоскости.
Кривая, точки которой не принадлежат одной плоскости называют пространственной.

Свойства кривой линии

Секущая – прямая m, пересекающая кривую в одной, двух и более точках.

Касательная к кривой в точке M – прямая t, являющаяся предельным положением секущей, проходящей через точку M и точку N кривой, при стремлении N→M.

Нормаль к плоской кривой в регулярной точке M – прямая n, перпендикулярная к касательной в точке M.

Плоская кривая, в каждой точке которой можно провести касательную, называется плавной кривой.

Если в некоторой точке кривой изменяется ее движение по касательной, то эта точка называетсяособой точкой.

Способы образования кривой

· кривая – это траектория движения точки (кинематический способ);

· кривая – это проекция некоторой кривой;

· кривая – это линия пересечения двух поверхностей;

· кривая – это линия пересечения поверхности плоскостью.

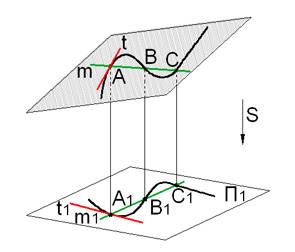
Проекционные свойства плоских кривых:

· порядок плоской алгебраической кривой при параллельном проецировании не изменяется;

· бесконечно удаленным точкам кривой соответствуют бесконечно удаленные точки ее проекций;

· касательная к кривой проецируется в касательную к ее проекции;

· число точек пересечения плоских кривых сохраняется при проецировании.

Поверхности вращения

Поверхности вращения образованы вращением образующей вокруг неподвижной оси. Каждая точка образующей описывает около оси окружность, и, следовательно, любая плоскость, перпендикулярная оси, пересечет поверхность вращения по окружности – параллели. Параллель максимального радиуса называется экватором.Плоскость, проходящая через ось поверхности вращения, пересекает поверхность по меридиану. Главный меридианполучается при проведении через ось фронтальной плоскости уровня. Точка, принадлежащая поверхности, расположена на некоторой линии, принадлежащей поверхности, например, параллели или образующей.

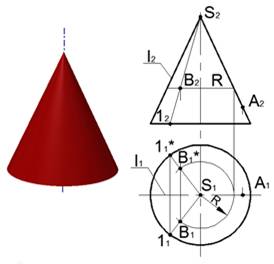
Конусобразуется вращением прямой m, проходящей через точку S на оси I

На чертеже по заданным проекциям A1 и B2 точек, принадлежащих конической поверхности, найдены проекции A2 и B1. Построение выполнено при помощи крайней правой образующей (S−A) и образующей (S−1), проведенной через точку B. Можно построить недостающую проекцию точки B и с помощью параллели радиуса R.

Цилиндробразуется вращением прямой L, параллельной оси, вокруг этой оси I.

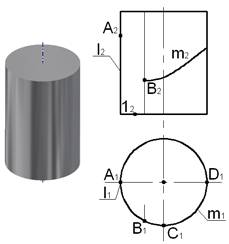
На чертеже цилиндра, ось которого перпендикулярна Π1, для построения проекций точек кривой линии m, принадлежащей поверхности цилиндра, использованы образующие цилиндра, проходящие через точки кривой.

Сфера образуется вращением окружности вокруг оси I, проходящей через центр окружности.

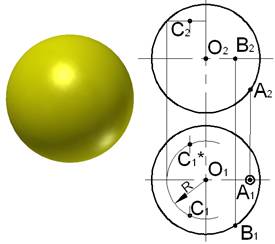
На чертеже сферы по фронтальным проекциям точек A, B, C найдены их горизонтальные проекции. Проекция точки A1 построена по условию принадлежности точки главному меридиану сферы. Точка B принадлежит экватору сферы. Для определения C1 построена горизонтальная проекция параллели, проходящей через точку C, параллель радиуса R.

Тор открытый – ось вращения расположена в плоскости окружности и не пересекает ее.

На чертеже одной четвертой части тора, ось которого перпендикулярна Π1, показано построение проекций точек, принадлежащих поверхности. Точки A и B расположены на экваторе тора. Фронтальной проекции C2 точки C соответствуют две горизонтальные проекции C1 и C∗1 на задней и передней части тора, расположенные на параллелях радиусов R и R∗.

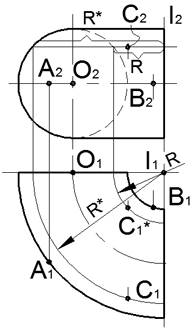
Тор закрытый – ось вращения расположена в плоскости окружности и совпадает с ее хордой.

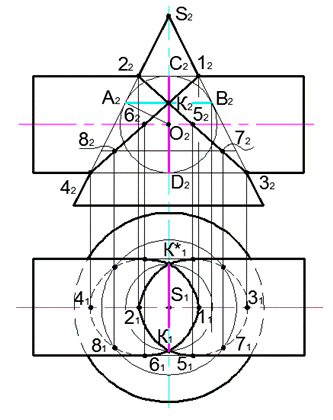
Теорема Г. Монжа

Если две поверхности второго порядка описаны около третьей или вписаны в неё, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания.

Два цилиндра, горизонтально проецирующий и фронтально проецирующий, описаны около одной сферы.

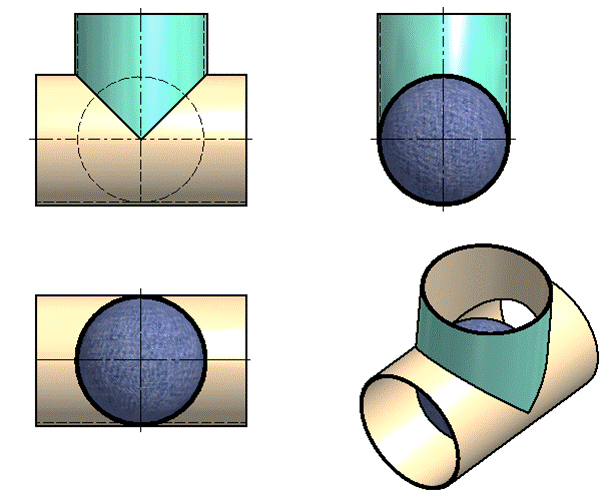
Построим проекции линии пересечения конуса и цилиндра, описанных около одной сферы.

Центр сферы, вписанной в конус и цилиндр, находится в точке О пересечения их осей.

Конус касается сферы по окружности, фронтальной проекцией которой является отрезок (A2 − B2).

Цилиндр касается сферы по окружности, которая на Π2 проецируется в отрезок (C2 − D2).

В пересечении (A2 − B2) и (C2 − D2) получена точка K2. В точку K2 проецируется линия K − K∗, которая соединяет точки касания заданных поверхностей.

Линия пересечения поверхностей распадается на два эллипса, которые на фронтальную плоскость проекций проецируются в прямые, проходящие через точки пересечения очерков конуса и цилиндра –(22 – K2 – 32) и (42 – K2 – 12).

Горизонтальная проекция линий пересечения конуса и цилиндра построена из условия принадлежности линий поверхностям. Точки 5, и 61 принадлежат очерковым образующим конуса и цилиндра и определяют границу видимости на Π1.

Я.М. Стрек, Ю.А. Стрек

Конспект лекций по начертательной геометрии

Якутск 2016

Оглавление

Методы проецирования.. 3

Инвариантные свойства параллельного проецирования.. 5

Ортогональный чертеж точки.. 9

Ортогональный чертеж прямой.. 14

Длина отрезка прямой, углы его наклона к плоскостям проекций. Способ прямоугольного треугольника.. 17

Ортогональный чертеж плоскости.. 18

Плоскости общего и частного положения.. 19

Принадлежность точки и линии плоскости. Главные (особые) линии плоскости 21

Пересечение прямой линии с плоскостью... 25

Пересечение плоскостей.. 26

Прямые и плоскости, параллельные плоскости.. 29

Прямые и плоскости, перпендикулярные плоскости.. 30

Способы преобразования чертежа. Метрические задачи.. 34

Замена плоскостей проекций.. 34

Плоскопараллельное перемещение. Вращение.. 38

Вращение вокруг проецирующих прямых.. 39

Вращение вокруг прямых уровня.. 40

Совмещение.. 42

Плоские кривые линии. Кривые второго порядка.. 45

Свойства кривой линии.. 45

Способы образования кривой.. 45

Проекционные свойства плоских кривых:. 46

Проекционные свойства пространственных кривых.. 46

Алгебраические кривые второго порядка рассматривают как плоские сечения поверхности конуса.. 47

Пространственные кривые линии. Винтовые линии.. 47

Поверхности вращения.. 48

Сечение поверхностей плоскостью... 50

Пересечение прямой линии с поверхностью... 51

Обобщенные позиционные задачи.. 53

Способ вспомогательных секущих плоскостей.. 53

Способ вспомогательных концентрических сфер.. 56

Частные случаи пересечения поверхностей второго порядка.. 58

Теорема Г. Монжа.. 58

Приближенные развертки развертывающихся поверхностей.. 62

Методы проецирования

Метод проецирования применяется для изображения геометрического объекта на плоскости. Изображение получается при пересечении проецирующих лучей с плоскостью.

Центральное проецирование.

Проецирующие лучи проводятся из одной точки S – центра проекций. Π1 – плоскость проекций, точки A, B, C, D – точки пространства, D∈Π1; SA, SB – проецирующие лучи.

A1, B1, C1, D1 – центральные проекции точек A, B, C, D на плоскости проекций Π1; D1≡D.

Выводы:

1. Каждой точке пространст