Вычисление площади полной и боковой оверхности куба и любого прямоугольного параллелепипеда

После знакомства учащихся с полной и боковой поверхностями любого прямоугольного параллелепипеда, с их развертками учитель может, опираясь на имеющиеся знания учащихся о вычислении площадей фигур, показать, как вычисляются площади полной и боко­вой поверхностей. Поскольку куб является частным случаем паралле­лепипеда, то, казалось бы, целесообразнее было бы сначала по­знакомить учащихся с формулой вычисления площади полной и боковой поверхностей любого прямоугольного параллелепипеда, а на основании этого дать соответствующие формулы для куба. Однако опыт показывает, что учащимся в данном случае легче усваивать знания от частного к общему, т. е. необходимо идти от более знакомого и простого геометрического тела — куба к любому прямо­угольному параллелепипеду. Поэтому подводим их вначале к'выводу формулы вычисления площадей полной и боковой поверхностей. Еще раз рассматривая куб, дети вспоминают, сколько граней он имеет, какую геометрическую фигуру представляет собой каждая грань куба. Учащиеся отмечают, что каждая грань куба — квадрат. Вспоминают, как вычисляется площадь квадрата. Поверхность куба состоит из 6 граней, т. е. 6 одинаковых квадратов. Отсюда уча­щиеся путем наводящих вопросов подводятся к выводу: чтобы вычислить площадь полной поверхности куба, необходимо вычислить площадь одной грани куба и результат (произведение) умножить на 6. Площадь боковой поверхности куба учащиеся могут вычислить самостоятельно. Только для этого необходимо, чтобы они зрительно воспринимали куб или его развертку.

Например, нужно вычислить площадь полной (боковой) поверх­ности куба с длиной ребра 5 см. Площадь одной грани — 5 кв. см х 5 = 25 кв. см. Площадь одной полной поверхности — 25 кв. см х 6 =150 кв. см. Площадь боковой поверхности — 25 кв. см. х 4 = = 100 кв. см.

Наиболее сильных учащихся, которых учитель на предыдущих уроках познакомил с формулой вычисления площади квадрата, можно познакомить с формулой вычисления площади полной и боковой поверхностей куба и параллелепипеда. С этой целью учитель просит записать формулу вычисления площади квадрата, т. е. грани куба, если его ребро обозначить буквой a: S _грани = a². Полная поверхность состоит из б граней, значит, S _{полн. куба} = 6 а². Боковая поверхность куба состоит из 4 таких граней, значит, S_{6oк куба} = 4а².

Далее учащиеся подводятся к выводу формул вычисления пло­щадей полной и боковой поверхностей любого прямоугольного парал­лелепипеда. Снова рассматривается прямоугольный параллелепипед и выделяются попарно одинаковые грани. Грани, составляющие полную поверхность: два основания, передняя и задняя, левая и правая боковые грани. Площадь передней грани может бытьполуче­на умножением длины на высоту. Площадь левой (или правой) боковой грани — умножением ширины на высоту, площадь основа­ния — умножением длины на ширину.

Площадь полной поверхности прямоугольного параллелепипеда получим, если площадь каждой из трех перечисленных граней умножим на 2 и найдем сумму полученных произведений.

Площадь боковой поверхности параллелепипеда (S_{6oк паралл}) по­лучим, если площадь передней грани умножим на 2, а затем площадь одной боковой грани умножим на 2 и полученные произве­дения сложим.

Если длину параллелепипеда обозначим буквой а, ширину — b, высоту — h, то формула вычисления полной поверхности будет за­писана так:

S _{полн. паралл=} ah х2 + bh х 2 + ab х 2

Площадь боковой поверхности получится, если из площади пол­ной поверхности вычесть площадь основания, умноженную на 2:

S_{6oк паралл} = ah х2 + bh х 2.

Данные формулы могут бытьпреобразованы:

S _{полн. паралл=}2 (ah + bh + аb),

S_{6oк паралл} = 2(ah + bh).

Для сознательного выполнения учащимися вычисленияплощади полной или боковой поверхности куба и любого прямоугольного

параллелепипеда необходимо предлагать им модели этих геометри­ческих тел, чтобы дети получили размеры путем измерения ребер, требовать от них чертежа развертки и только после этого давать задание на вычисление площадей боковой и полной поверхностей. От вычисления площади поверхностей моделей следует перейти к вычислению площадей стен классной комнаты, площади листа бума­ги, который потребуется на оклейку стенок коробки (снаружи, изнутри), и т. д.

Для учащихся, с трудом овладевающих математическими зна­ниями, самостоятельное вычисление площадей полной и боковой поверхностей параллелепипеда необязательно.

Наиболее способных к математике учащихся учитель знакомит с изготовлением развертки цилиндра(под руководством учителя). С этим материалом можно познакомить учащихся на кружке мате­матики.

Предъявляется модель цилиндра. Учитель просит получить из модели цилиндра его развертку. Сначала выслушивает учеников, как бы они это сделали, т. е. проверяет, как учащиеся могут использо­вать свой прошлый опыт в получении разверток любого прямоуголь­ного параллелепипеда для изготовления развертки нового тела. Для отдельных учащихся трудность возникает при вырезании из моделей цилиндра оснований. Учитель оказывает ученикам практи­ческую помощь. Когда модель разрезана, ученики получают два кру­га — основания и прямоугольник — боковую поверхность. Ученикам надо объяснить, что две стороны прямоугольника (боковой поверх­ности цилиндра) являются высотами цилиндра, две другие сторо­ны — «выпрямленными» окружностями оснований. Свертывая прямоугольник, учащиеся могут проверить, что длина стороны прямо­угольника равна длине окружности основания. Формула длины окружности известна учащимся. Зная радиус (диаметр) основания, они могут ее вычислить.

Таким образом, чтобы начертить развертку цилиндра, учащиеся должны располагать двумя размерами: радиусом круга, лежащего в основании, и высотой цилиндра. Последовательность работы: 1) из­меряется радиус основания цилиндра; 2) вычисляется длина окруж­ности основания; 3) измеряется высота цилиндра; 4) вычерчивается прямоугольник со сторонами, длины которых равны длине окруж­ности и высоте данного цилиндра; 5) вычерчиваются окружности (границы оснований), по одной с каждой стороны прямоугольника (боковой поверхности); 6) по длине окружностей располагаются припуски, необходимые для склеивания модели.

Особую трудность будет представлять изготовление модели по образцу, когда радиус основания и высоту цилиндра требуется по­лучать путем измерения. Высота цилиндра измеряется с помощью чертежного треугольника, который располагается так, как показано на рисунке 53. Затем определяется диаметр основания с помощью прямого угла чертежного треугольника, вписанного в окружность основания. Чертежный треугольник располагается так, как показано на рисунке 54. Точки пересечения сторон прямого угла с окружностью

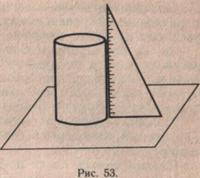являются концами диаметра. Прове­дя диаметр и разделив его пополам, учащиеся получат длину радиуса основания (рис. 54).

Под руководством учителя уча­щиеся знакомятся с вычислением площади боковой и полной поверх­ностей цилиндра.

Путем беседы выясняется еще раз, что прямоугольник является разверткой боковой поверхности ци­линдра, что является высотой и ос­нованием этого прямоугольника. Учащиеся подводятся к выводу: чтобы вычислить площадь бо­ковой поверхности цилиндра, надо основание прямоугольника ум­ножить на высоту. Высоту цилиндра можно измерить, а дли­ну основания прямоугольника надо вычислить, так как это дли­на окружности основания цилиндра. Если длину окружности обозначить С, высоту — h, площадь боковой поверхности — S, то получим формулу вычисления площади боковой поверхности цилиндра:

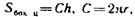
где г — радиус основания цилиндра.

Следующим этапом в вычислении площадей поверхностей может быть пирамида и вычисление площадей ее боковой и полной по­верхностей.

Чтобы получить формулу вычисления площади поверхности ци­линдра, учитель выясняет, какие фигуры составляют его полную поверхность. Учащиеся по развертке устанавливают, что полная поверхность цилиндра состоит из прямоугольника и двух кругов, лежащих в основании цилиндра. Следовательно, если к площади бо­ковой поверхности прибавить площади двух оснований (кругов), то получим площадь полной поверхности цилиндра. Формула площади круга (S_Kp==nr²) учащимся известна.

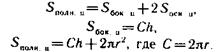Сначала учитель показывает школьникам полые модели пирамид с различными правильными многоугольниками в основании, но рассекает их одним способом — по боковым ребрам.

На модели пирамиды с квадратом в основании и ее развертке рассматриваются боковая и полная поверхности. Учащиеся сами должны установить, что боковая поверхность пирамиды состоит из четырех граней или треугольников, полная поверхность состоит из боковой поверхности и основания.

Развертку пирамиды можно изготовить следующим способом (но данный материал не является обязательным для всех уча­щихся) .

Пирамида разрезается по всем четырем боковым ребрам, полу­чается развертка вида, как на рисунке 55.

Под руководством учителя учащиеся выводят формулы площадей полной и боковой поверхностей пирамиды. Площадь боковой поверх­ности — это сумма площадей четырех боковых граней, каждая из которых является равнобедренным треугольником:

(а — ребро в основании, h — высота боковой грани, – площадь боковой грани).

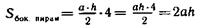
Полная поверхность складывается из боковой поверхности и осно­вания:

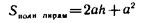
(а² — площадь основания).

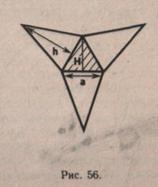
Если правильная пирамида имеет в основании треугольник, то рассматривается следующий способ построения чертежа развертки (рис. 56).

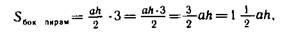Под руководством учителя, так же как и в предыдущем случае, учащиеся знакомятся с выводом формул:

(а — ребро основания, h — высо­та боковой грани, –

площадь

боковой грани; Н — высота осно­вания, –

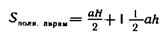
площадь основания).

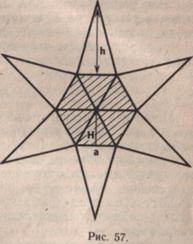
Если правильная пирамида имеет в основании шестиугольник, то рассматривается такой способ построения чертежа развертки пи­рамиды как на рисунке 57.

Построение всех разверток пи­рамид выполняется одинаково: задаются длины ребра основания и бокового ребра. Сначала строится основание (квадрат, равносторонний треугольник, правильный шестиугольник) поданной стороне — ребру основания. Затем строят­ся равнобедренные треугольники — боковые грани по данному боко­вому ребру (основание у треугольников уже имеется).

Для более полного знакомства школьников с конусомполая модель конуса разделяется на боковую поверхность и основание, затем боковая поверхность разрезается по образующей. Таким образом будет получен круг — основание и сектор большего круга — боковая поверхность. Радиус основания легко измерить, можно вы­числить площадь основания и длину окружности основания. Окруж­ность основания соответствует дуге боковой поверхности. Радиус дуги — это длина образующей конуса.

Учащиеся не могут сами изготовить развертку конуса, но, по­лучив готовую развертку от учителя, должны сложить и склеить модель конуса.

Возможно учащиеся смогут выполнить под руководством учителя следующую работу. Задается радиус круга. Круг делится на 3, 6, 2, 4 равных сектора. Зная радиус, дети вычисляют окружность, а значит, и дуги одного из секторов, вычисляют площадь круга и площадь взятого сектора.

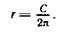Дополняем чертеж сектора кругом (основанием конуса). Таким образом получена полная поверхность, из которой можно получить модель конуса (не хватает только припусков для склеивания модели).

Этот сектор будет боковой поверхностью будущего конуса, ее площадь уже вычислена. Теперь необходимо найти радиус основания. Длина окружности основания известна — это длина дуги сектора. По формуле С = 2лг находим г:

Зная радиус основания, легко вычислить его площадь. Полная поверхность конуса будет равна сумме площади боковой поверх­ности (площадь сектора) и площади основания.

Еще раз отмечаем, что этот материал может быть дан во внеуроч­ное время наиболее подготовленным учащимся.

Понятие об объеме

Учащимся вспомогательной школы в школьных мастерских, в повседневной жизни нередко приходится сталкиваться с предметами, имеющими объем, сравнивать их по объему. Они вытачивают детали, различные по объему, выпиливают бруски, изготавливают коробки разного объема. Работая на школьном участке, учащиеся убеждают­ся в разном объеме ведер, бочек, ящиков и т. д.

Первое понятие об объеме, об измерении объема куба и любого прямоугольного параллелепипеда учащиеся получают на уроках математики.

На наглядных примерах надо показать им смысл слова «объем». Можно провести аналогию между словами «объем» и «вместимость», «ёмкость». Показать, что вместимость (объем) тел может быть либо различной, либо одинаковой.

Вначале можно показать различную вместимость двух банок — литровой и полулитровой. «Вода, налитая в литровую банку,— говорит учитель,— полностью не вмещается в полулитровую бан­ку, значит, вместимость, или, еще можно сказать, объем, литровой банки больше, чем вместимость, или объем, полулитровой банки». Затем следует сравнить объемы двух коробок, имеющих форму параллелепипеда. В одну коробку насыпать песок или опилки, заполнить ее до краев. Содержимое коробки пересыпать в другую коробку. Она оказалась неполной. Значит, объем второй коробки больше, чем первой.

Наконец, можно сравнить объемы двух одинаковых спичечных коробок: «Наполним одну коробку песком. Пересыпем ее содержи­мое в другую коробку. Песок заполнил вторую коробку. Можно сказать, что эти коробки имеют одинаковый объем».

Учитель показывает учащимся параллелепипеды различных раз­меров и просит сравнить «на глаз» их объемы. Сравниваются объемы окружающих предметов: шкафов, аквариумов, классных комнат, зданий и т. д. Но суждения учащихся могут оказаться неточными.

«Чтобы измерить объем какого-либо тела,— говорит учитель,— нужно иметь единицы измерения объема (меры объема)». Уча­щиеся вспоминают меры длины, меры площади. Объем должен из­меряться мерами объема. Учитель показывает меру объема — куб с ребром в 1 см — это кубический сантиметр. Кубические сан­тиметры получает (из арифметического ящика) каждый ученик. Учитель спрашивает, как называется это геометрическое тело, про­сит измерить ребро, рассказать, что же называется кубическим сантиметром. В заключение учитель сам дает определение куби-

ческого сантиметра и знакомит с записью: 1 куб. см или 1 см³.

Можно сразу познакомить учащихся с другими единицами из­мерения объема и дать их соотношения. Но, учитывая, что учащиеся вспомогательной школы долго не запоминают, смешивают между собой единицы измерения объема и путают их с единицами изме­рения длины и площади, целесообразнее, как показывает опыт, позна­комить их с измерением объема параллелепипеда пока только ку­бическими сантиметрами, а уже потом познакомить с другими единицами измерения объема.

Сначала кубическими сантиметрами заполняется коробка, имею­щая форму прямоугольного параллелепипеда (коробка заранее из­готовляется так, чтобы в ней уместилось целое количество куби­ческих сантиметров). Кубические сантиметры укладываются по длине коробки (например, не уложилось 5), затем выкладывается все дно коробки и подсчитывается количество рядов (например, их 3), получился один слой кубических сантиметров — 15 куб. см. Затем такие же слои укладываются по высоте коробки, пока не заполнят ее. Подсчитывается число слоев (например, их 4). Чтобы определить общее число кубических сантиметров в коробке, нужно 5 куб. см умножить на число рядов. Получим число кубических сантиметров в слое. Это число умножим на 4, т. е. на количество слоев,— и будет объем коробки. V_napaлл„ = 5 куб. см х 3 х 4=60 куб. см.

Далее учащиеся получают задание: «Положить в ряд 3 куб. см. Какое геометрическое тело получилось? Каков объем этого парал­лелепипеда? Каковы его длина, ширина, высота?» Учащимся пред­лагается сложить из кубических сантиметров параллелепипеды оп­ределенных размеров и вычислить их объемы.

Таких упражнений учащиеся должны сделать достаточно много, чтобы учитель мог подвести их к обобщению: в параллелепипеде по длине укладывается столько кубических сантиметров, какова длина этого параллелепипеда в сантиметрах; в одном слое столько рядов, какова ширина этого параллелепипеда; слоев столько, какова его высота. Следовательно, чтобы вычислить объем параллелепипеда, нужно измерить его длину, ширину и высоту, полученные числа перемножить и результат выразить в кубических мерах (мерах объема).

Если длину параллелепипеда обозначить буквой а, ширину — Ь, высоту — h, объем — V, то формулу вычисления объема параллеле­пипеда можно будет записать так: V = a х b х h (куб. ед).

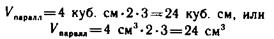Так как учащиеся знают свойства куба, сходство и различие куба и любого другого прямоугольного параллелепипеда, то нетрудно подвести учащихся к выводу формулы вычисления объема куба:

Запись при вычислении объема параллелепипеда (вычислить объем параллелепипеда, длина которого 4 см, ширина 2 см и высота 3 см) по формуле может быть такой:

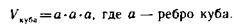
Учитель показывает и другую запись формулы вычисления объема куба: V_Ky6a = a³.

Но знакомить учащихся с формулами вычисления объема па­раллелепипеда (куба) необязательно. Их можно сообщить только сильным учащимся или познакомить с ними членов математического кружка.

Далее учитель показывает учащимся необходимость более круп­ных единиц измерения объема и знакомить их с кубическими де­циметрами и кубическими метрами по аналогии с кубическими сантиметрами. Эти меры должны быть изготовлены в натуральную величину.

Чтобы учащиеся могли более отчетливо представить себе со­отношения между единицами кубических мер, следует пользоваться рисунками, на которых кубический метр разбит на кубические дециметры, кубические дециметры — на кубические сантимет­ры и т. д.

На моделях кубического дециметра и кубического метра их ребра должны быть соответственно разделены на сантиметры и дециметры.

Учащиеся решают готовые и составляют сами задачи на вычисле­ние объема куба и параллелепипеда.

Несмотря на то что единицы измерения объема, площади и ли­нейные единицы вводятся не одновременно, многие учащиеся даже в IX классе слабо их различают, смешивают, неправильно назы­вают и записывают наименования. Необходимым пособием в классе должна быть таблица линейных, квадратных, кубических мер, ряд единиц мер должен быть изображен в натуральную величину: сан­тиметр, квадратный сантиметр и т. д.

Когда учащиеся решают примеры и задачи, в которых указаны линейные, квадратные и кубические меры, они должны показать единицы этих мер на таблице. Чаще следует ставить перед учащимися вопросы, при ответе на которые они должны выбирать меру. Напри­мер, Какими мерами измеряется: 1) длина ткани, длина гвоздя, длина, высота и ширина бруска; 2) площадь картона, доски, класса, огорода, поля, помещения для скота; 3) объем бруска, шкафа, сарая, зернохранилища, коровника и т. д.?