Развертка куба и любого прямоугольного параллелепипеда

Опыт показывает, что знакомство с разверткой параллелепипеда во вспомогательной школе целесообразно начать с развертки куба, так как учащимся ее легче вычертить и изготовить мо­дель.

Изучение развертки куба начинается с рассмотрения куба, изго­товленного из картона или плотной бумаги. Учитель сообщает, что поверхность всех граней куба составляет его полную поверх­ность, моделью которой является развертка куба. Поверхность че­тырех боковых граней куба составляет его боковую поверхность. «Сегодня на уроке вы будете учиться вычерчивать и вырезать раз­вертку куба»,— говорит учитель. Каждый ученик получает мо­дель куба и разрезает ее по тем ребрам, которые указывает

учитель.

Учитель осуществляет показ. Целесообразно модель разрезать по ребрам, принадлежащим верхнему и нижнему основаниям. В этом случае боковые грани будут расположены последовательно друг за другом, верхнее основание будет помещено над одной из боковых граней, нижнее основание под этой гранью.

Учащимся сообщается: получилась развертка куба или модель полной поверхности куба. Куб развернули, получили развертку. Если снова сложить развертку, то получим куб. Опыт показывает, что боковые грани модели следует закрасить одним цветом, а верх­нее и нижнее основания — другим. Можно выделить цветом перед­нюю и заднюю, а также левую и правую боковые грани. В этом случае учащимся легче узнавать соответствующие грани на разверт­ке. Нужно выполнить побольше упражнений с той разверткой, кото­рая получена при разрезании модели куба. Оставляя нетронутыми четыре грани (боковые), учитель предлагает отрезать основания и поместить их на новое место. Учащиеся убеждаются, что основания могут быть прикреплены к любой из боковых граней.

Далее необходимо познакомить их с составными частями и раз­мерами развертки и планом работы над изготовлением чертежа развертки: 1) определить общее количество боковых граней, каж­дая из которых — квадрат; 2) вычислить длину прямоугольника, составленного из четырех боковых граней; 3) определить ширину этого прямоугольника; 4) установить количество и размер квадратов

(оснований), которые располагаются над и под какой-либо из бо­ковых граней.

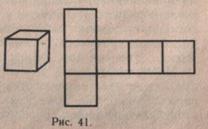
Когда все детали развертки и их размеры установлены, школь­ники под руководством учителя приступают к построению черте­жа развертки (рис. 41).

Начать вычерчивание развертки надо с построения прямоуголь­ника, который представляет собой боковую поверхность куба. Опыт показывает, что если учащиеся будут последовательно вычерчивать один квадрат за другим, то у них никогда из четырех боковых граней не получится прямоугольник. Чтобы сразу изобразить боко­вую поверхность в виде прямоугольника, ученики должны определить его размеры: измерить ребро куба, полученное число умножить на 4. Это длина прямоугольника, а ширина его равна длине ребра. Затем прямоугольник надо разделить на четыре равных квадрата. Сверху и снизу к прямоугольнику пристраиваются квадраты — ос­нования. Оставив на время чертеж, школьники снова возвраща­ются к развертке куба. Они складывают из развертки куб. Учи­тель сообщает, что куб надо не только сложить из развертки, но и склеить, а для этого необходимо сделать припуски на гранях куба. Разбирается, где эти припуски должны быть. После этого школьники на чертеже развертки вычерчивают необходимые при­пуски. Когда чертеж готов, учащиеся вырезают развертку. Согнув развертку по ребрам, дети складывают модель куба. Не стоит спешить со склеиванием куба, так как еще не раз нужно будет «развернуть развертку», чтобы вспомнить место каждой из граней. Учащиеся убеждаются, что развертка куба состоит из шести оди­наковых квадратов. Каждый учащийся должен заготовить шесть одинаковых квадратов и поупражняться в составлении из них развертки.

Теперь от учеников требуется по модели куба сделать чертеж его развертки с необходимыми припусками. Например, требуется сделать чертеж развертки куба с ребром 5 см. Сначала ученик за­готовляет 6 квадратов — граней куба со стороной, равной 5 см. Раскладывает их так, чтобы получилась развертка (рис. 41).

Далее учащимся предлагается куб. По образцу ранее из­готовленной развертки они делают чертеж новой развертки этого куба. Учащихся надо учить предварительно составлению, обдумыва­нию плана работы над чертежом развертки куба.

Предварительная выработка пла­на построения чертежа и предвари­тельные расчеты помогают детям быстро выполнить чертеж.

Только тогда, когда учащиеся овладеют приемами построения чер­тежа развертки куба, можно перейти к построению чертежа развертки любого прямоугольного параллеле­пипеда. Школьникам раздают модели прямоугольных параллелепипедов,

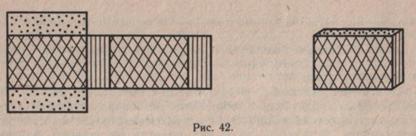
изготовленные из плотной бумаги. Они внимательно их рассматри­вают, выделяют грани и раскрашивают их попарно в одинаковый цвет (два основания, переднюю и заднюю, левую и правую боковые грани). Затем предлагается сделать разрезы по ребрам, примыкаю­щим к нижнему и верхнему основаниям (т. е. частично отделить основания от модели), и по одному боковому ребру. Получилась раз­вертка параллелепипеда (рис. 42).

На полученной развертке учащиеся находят все грани паралле­лепипеда. Складывая развертку, они снова получают модель па­раллелепипеда. Далее сравниваются модель и развертка параллеле­пипеда, устанавливается, где длина, ширина, высота параллеле­пипеда на модели и на развертке. Полученная развертка парал­лелепипеда сравнивается с аналогичной разверткой куба, чтобы выяснить, где должны располагаться припуски для склеивания модели.

По развертке параллелепипеда учащиеся изготавливают чертеж с такими же размерами. Подготовка детей к работе над черте­жом должна быть такой же, как и над чертежом развертки куба. Они составляют план работы над чертежом, снимают с готовой развертки размеры для чертежа. Сделав чертеж, учащиеся под ру­ководством учителя делают припуски для склеивания параллеле­пипеда, затем вырезают развёртку, сгибают по линиям чертежа, складывают, смазывают клеем припуски, склеивают и получают модель параллелепипеда. Так же, как и на развертке куба, осно­вания параллелепипеда могут менять свое положение относительно боковых граней. Учащиеся разрезают одну из разверток так, чтобы отделить верхнее и нижнее основания от боковой поверхности, и прикладывают их поочередно к каждой боковой грани.

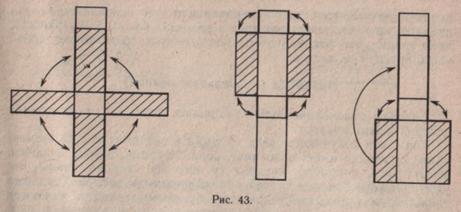
Затем они устанавливают размеры каждого из ребер, состав­ляют план вычерчивания развертки, изготавливают не одну, а не­сколько разверток с одними и теми же размерами, чтобы запомнить последовательность работы над чертежом. До складывания модели школьники сравнивают элементы разверток (квадраты, прямоуголь­ники) с гранями параллелепипеда (рис. 43).

После работы над разверткой одного параллелепипеда учитель предлагает учащимся изготовить развертки, а по ним модели новых параллелепипедов. Дается задание сделать чертежи разверток. С этой целью учащиеся определяют длину основания и боковой сто-

роны прямоугольника, который соответствует боковой поверхности параллелепипеда, определяют размеры оснований и делают чертеж развертки.

Цилиндр (прямой, круговой)

Во вспомогательной школе рассматривается только прямой, кру­говой цилиндр.

При ознакомлении учащихся с понятием цилиндра учитель прино­сит на урок модели цилиндров различного диаметра, различной высоты, изготовленных из разных материалов, предметы цилиндри­ческой формы; карандаш, стакан, кусок трубы, консервную банку и др. Учитель показывает модель цилиндра, выясняет, знают ли учащиеся название этого геометрического тела, спрашивает, отно­сится ли цилиндр к геометрическим фигурам или телам и почему.

Учащиеся рассматривают модели цилиндров, выделяют и назы­вают верхнее и нижнее основания, боковую поверхность.

Каждый ученик получает модель цилиндра. Учитель просит поста­вить цилиндр на лист бумаги (сначала одно основание, затем другое) и обвести основания карандашом. Накладывая основания цилиндра на эти круги, учащиеся приходят к выводу, что основания цилиндра — равные круги.

«Если соединить центры кругов — оснований,— говорит учи­тель,— то получим высоту цилиндра».

Конус (прямой, круговой)

При знакомстве учащихся с конусом учитель демонстрирует различные модели конусов, предметы, имеющие форму конуса (во­ронка, игрушечная пирамида, бумажный фунтик и т. д.).

Рассматривая модели конуса, дети устанавливают, что основанием конуса является круг. Отделив основание и разрезав боковую поверхность, дети увидят, что боковая поверхность конуса представляет собой часть круга, т. е. сектор.