Обучение элементам геометрии
М. Н.ПЕРОВА В. В. ЭК
ОГЛАВЛЕНИЕ
Введение ................................................................................................................... 3
Глава I. Общие вопросы содержания и методики изучения геометрического материалав курсе математики вспомогательной школы
1. Значение и задачи изучения геометрического материала..................................... 5
2. Содержание геометрического материала в курсе математики
вспомогательной школы.......................................................................................... 6
3. Основные трудности и некоторые особенности усвоения геометрических
знаний учащихся вспомогательной школы……………………………………….11
4. Связь геометрического материала в курсе математики с материалом других учебных предметов………………………………………………………………..14
5. Основные средства, методы и приемы изучения геометрического материала.
Пути формирования геометрических представлений…………………….……18
6. Основные вопросы организации изучения геометрического материала………..29
7. Учет и контроль знаний, умений и навыков но геометрии………………………42
Глава 2. Методика изучения геометрического материала
1.Точка. Линии............................................................................................................ 45
2. Круг. Окружность................................................................................................... 63
3. Углы.......................................................................................................................... 71
4. Многоугольники..................................................................................................... 80
5. Взаимное положение геометрических фигур на плоскости................................. 102
6. Симметричные и симметрично расположенные фигуры.
Ось, центр симметрии................................................................................................ 106
7. Геометрические тела............................................................................................... 112
8. Площади и объемы................................................................................................. 120
9. Задачи геометрического содержания.................................................................... 134
ОБУЧЕНИЕ ЭЛЕМЕНТАМ ГЕОМЕТРИИ
ВО ВСПОМОГАТЕЛЬНОЙ ШКОЛЕ
ПОСОБИЕ ДЛЯ УЧИТЕЛЯ
Рекомендовано
Главным учебно-методическим управлением
общего среднего образования Госкомитета СССР
по народному образованию
2-е издание, переработанное
МОСКВА
«ПРОСВЕЩЕНИЕ»
ББК 74.3 П27
Перова М. Н., Эк В. В.
П27 Обучение элементам геометрии во вспомогательной школе: Пособие для учителя.— 2-е изд., перераб.— М.: Просвещение, 1992.— 144 с: ил.— ISBN 5-09-004090-7.
В пособии раскрываются общие и частные вопросы содержания и методики обучения элементам геометрии в курсе математики вспомогательной школы, а также приводятся образцы решения задач геометрического содержания.
Для учителей вспомогательной школы. Может быть использовано студентами дефектологических факультетов пединститутов.
Первое издание вышло в 1983 году.
| 4310010000—177 103(03)—92 |
| ББК 74.3 |
Инф. письмо — 92, № 270
Учебное издание
ПЕРОВА Маргарита Николаевна ЭК Валентина Васильевна
ОБУЧЕНИЕ ЭЛЕМЕНТАМ ГЕОМЕТРИИ ВО ВСПОМОГАТЕЛЬНОЙ ШКОЛЕ
Зав. редакцией Т. С. Залялова
Редактор Т. В. Панфилова
Младший редактор О. Р. Басова
Художник В. В. Беляева
Художественный редактор JI. Н. Сильянов
Технический редактор С. С. Якушкина
Корректор М. Ю. Сергеева
ИБ № 14172
Сдано в набор 15.05.91. Подписано к печати 29.08.91. Формат 60 X 90'/ie. Бум.
офс. № 2. Гарнитура литературная. Печать офсетная. Усл. печ. л. 9,0. Усл. кр.-отт. 9,38.
Уч.-изд. л. 10,26. Тираж 19 800 экз. Заказ 62. Цена 1 руб.
Ордена Трудового Красного Знамени издательство «Просвещение» Министерства печати и массовой информации РСФСР. 129846, Москва, 3-й проезд Марьиной
рощи, 41. Саратовский ордена Трудового Красного Знамени полиграфический комбинат Министерства печати и массовой информации РСФСР. 410004, Саратов, ул. Чернышевского, 59.
© Издательство «Просвещение», 1983
| ISBN 5-09-004090-7 |
© Перова М. Н, Эк В. В., 1992, с изменениями
ВВЕДЕНИЕ
Методическое пособие предназначается для учителей вспомогательных школ, а также студентов дефектологических факультетов педагогических институтов.
К пособии раскрываются вопросы обучения элементам геометрии учащихся вспомогательной школы. Наглядная геометрия является составной частью математики, изучаемой во вспомогательной школе.
На изучение ее отводится в соответствии с программой по математике во вспомогательной школе значительное количество часов.
Изучение этого раздела математики позволяет формировать у умственно отсталых школьников пространственные и геометрические представления и понятия, чертежные, измерительные и графические умения и навыки. Знания и умения, получаемые учащимися при изучении геометрии, не только обогащают их жизненный опыт, пополняют математический кругозор. Кроме того, эти знания играют большую роль в коррекции и компенсации дефектов умственного и эмоциональио-волевого развития учащихся, подготовке их к производительному, общественно полезному труду, к социальной адаптации и реабилитации.
В пособии наряду со специфическими методами и приемами формирования геометрических знаний, умений и навыков читатели познакомится и с коррекционными приемами, которые необходимо использовать при изучении геометрического материала, а также методикой решения различных видов задач геометрического содержания. Методическое пособие состоит из двух глав: общих вопросов содержания и методики изучения геометрического материала и вопросов частной методики.
И первой главе пособия излагаются задачи, содержание и организация изучения геометрического материала на уроках математики как в младших, так и в старших классах вспомогательной школы, показана взаимосвязь изучения арифметического и геометрического материала.
На основе собственного опыта, специальных исследований и анализа учебно-воспитательного процесса во вспомогательной школе авторы знакомят читателя с основными трудностями усвоения геометрического материала умственно отсталыми учащимися, вскрывают причины этих трудностей и намечают пути их предупреждения и решения. И этой же главе приводятся примерные планы и конспекты уроков разного типа, раскрываются требования к домашним заданиям, ведению тетрадей.
Вторая глава пособия посвящена вопросам частной методики изучения отдельных тем геометрического содержания.
В целях избежания повторов изложение методики изучения геометрического материала проводится не по классам, а по основным темам программы. Например, сначала излагается методика изучения таких геометрических фигур, как точки, линии, отрезки, затем углы, далее методика изучения многоугольников и т. д. Причем при изложении методики изучения каждой темы авторы стремятся показать содержание, методы и приемы работы над ней в каждом классе вспомогательной школы. Отмечают постепенно усложняющийся уровень требований к знаниям, умениям и навыкам учащихся, показывают все новые виды наглядных пособий и дидактическою материала, использование коррекционных приемов.
Такое изложение материала поможет учители) проследить постепенное усложнение содержания геометрическою материала от класса к классу, различный уровень требований к нижним учащихся по данному разделу математики и тем самым правильно выбрать
соответствующие методы и приемы изучения элементом наглядной геометрии.
Особое внимание авторы обращают на формирование навыков работы с измерительными и чертежными инструментами на уроках математики, учитывая, что эти навыки позволят подготовить учащихся к жизни и играют исключительно большую кoppекционную роль.
Обе главы пособия взаимосвязаны. Внимательное ознакомление с содержанием первой главы позволит правильно выбрить наглядные пособия, методы и приемы обучения и организационно правильно реализовать рекомендации, изложенные во второй главе пособия,
Авторы надеются, что пособие окажет помощь студенту – будущему учителю-олигофренопедагогу и учителю, не имеющему опыта работы с умственно отсталыми детьми.
В настоящем пособии невозможно привести методические рекомендации по всем частным вопросам, описать все трудности, которые могут встретиться учителю. Авторы сделали попытку на большом количестве основных программных тем, изучаемых во вспомогательной школе, показать особенности использования традиционных и специфических методов и приемов обучения умственно отсталых школьников элементам геометрии.
При подготовке методического пособия учитывались рекомендации, изложенные в методических пособиях Н.Ф. Кузьминой-Сыромятниковой, П. Г. Тишина, а также новые научные данные, полученные в исследованиях Ю. Т. Матасова, В. П. Гриханова, собственных исследованиях авторов, изучении опыта работы учителей вспомогательных школ.
Предисловие и глава I написаны М. Н. Перовой, глава II написана совместно М.Н.Перовой и В.В. Эк.
Глава 1
ОБЩИЕ ВОПРОСЫ СОДЕРЖАНИЯ И МЕТОДИКИ
В КУРСЕ МАТЕМАТИКИ
ВСПОМОГАТЕЛЬНОЙ ШКОЛЫ
ОСНОВНЫЕ ВОПРОСЫ ОРГАНИЗАЦИИ
V. Задание на дом.
Урок закрепления знаний(IX класс).
Тема урока. Куб как частный случай прямоугольного параллелепипеда.
Цель урока. Систематизировать знания учащихся о параллелепипеде. Показать, что куб — это параллелепипед.
Оборудование. Модели кубов, других параллелепипедов, их развертки (для демонстрации), шесть квадратов для составления развертки куба, шесть попарно равных прямоугольников для составления развертки параллелепипеда, линейки чертежные, треугольники, ножницы.
Ход урока.
(У учителя и у каждого ученика имеются модели куба и прямо-мольного параллелепипеда иного вида.)
1. Учитель просит показать вершины параллелепипеда. Спрашивает:
«Что показали? Что можно сказать о количестве вершин парал 
лелепипеда» Ученики отвечают: «Вершины — это точки. У параллелепипеда 8 вершин».
Учитель просит показать ребра параллелепипеда. Спрашивает: «Что показали? Что можно сказать о ребрах параллелепипеда?» Ученики отвечают: «Ребра — это отрезки. У параллелепипеда 12 ребер». Учитель просит показать равные ребра.
Далее учитель просит показать грани параллелепипеда. Спрашивает: «Что показали? Что можно сказать о гранях параллелепипеда?» Ученики отвечают: «У параллелепипеда 6 граней». Учитель просит показать равные грани.
После этого школьники повторяют все то, что им известно о параллелепипеде (8 вершин, 12 ребер, каждые четыре ребра равны между собой, 6 граней, каждые две грани являются равными между собой прямоугольниками).
Учитель показывает куб и говорит учащимся, что это параллелепипед, так как у него тоже 8 вершин, 12 ребер, 6 граней, только все ребра и грани у этого параллелепипеда равны.
II. Далее закрепляется изготовление разверток параллелепипедов разных видов.
Учитель предлагает учащимся: взять шесть квадратов и сложить из них развертку куба; взять шесть прямоугольников и сложить из них развертку параллелепипеда. (В слабом классе прямоугольники — грани параллелепипеда — могут иметь номера.)
III. Учитель спрашивает, как расположены друг относительно
друга грани в развертках. Школьники указывают, что четыре боковые
грани составляют один прямоугольник, над ним и под ним находятся основания.
Учитель указывает на четыре боковые грани куба и отличного от него параллелепипеда и просит рассказать, что это за грани, как вычислить их площадь, как называется их общая площадь. Дети отвечают, что это передние и задние, левые и правые боковые грани. Чтобы вычислить их общую площадь для куба, надо площадь одной грани умножить на четыре. Чтобы вычислить их общую площадь для любого параллелепипеда, надо найти площадь передней и одной боковой граней, сложить полученные числа, а сумму умножить на два. Вычисленная площадь боковых граней и будет площадью боковой поверхности параллелепипеда (куба). Затем аналогичная беседа проводится о площади полной поверхности параллелепипеда (куба).
IV. С помощью прямоугольников — моделей граней — рассматриваются различные положения оснований по отношению к боковым граням.
На развертке параллелепипеда дети указывают одинаковые по длине ребра (при перемещении оснований это особенно важно).
V. Детям раздаются две модели — модель куба и модель отличного от него параллелепипеда (одинаковые для всех учащихся). Они измеряют на моделях длины ребер. Вычерчивают развертки, выкраивают их, сгибают по ребрам и получают новые модели этих тел.
VI. Учащиеся решают задачи на вычисление площадей боковой и полной поверхностей прямоугольного параллелепипеда и записывают
вычисления в тетрадях (сильные ученики решают самостоятельно, слабые — с помощью учителя).
VII. Учитель просит рассказать об элементах прямоугольного параллелепипеда, свойствах его граней и ребер. Спрашивает, какие грани образуют боковую, полную поверхность, как получить развертку параллелепипеда (куба).
Контрольная работа, которой будет заканчиваться II четверть в IX классе, должна подвести итог изучению прямоугольного параллелепипеда, его поверхности. Примерное содержание контрольной работы может быть следующим.
Урок проверки знаний(IX класс).
Тема урока. Прямоугольный параллелепипед (куб). Цель урока. Проверить знание учащимися элементов параллелепипеда (куба), умения сделать чертеж развертки, вычислить площади боковой и полной поверхностей параллелепипеда.
Оборудование. Модели параллелепипедов, линейки, чертежные треугольники.
Содержание контрольной работы.
I. 1) Сделайте чертеж развертки куба, ребро которого равно 4 см.
2) Сделайте чертеж развертки параллелепипеда, длина основания которого 5 см, ширина 3 см, высота 4 см.
II. 1) Вычислите площади боковой и полной поверхностей куба, если длина его ребра равна 5 см.
2) Вычислите площади полной и боковой поверхностей параллелепипеда, у которого длины ребер равны 2 см, 5 см, 7 см.
III. 1) Вычислите площади полной и боковой поверхностей куба по данной модели, выполнив сначала измерения. (У каждого ученика своя модель.)
2) Вычислите площади боковой и полной поверхностей параллелепипеда по данной модели, выполнив измерения. (У каждого ученика своя модель.)
IV. Сделайте чертеж развертки куба, развертки параллелепипеда по данным моделям. (Каждый ученик имеет свои модели.) Модели для выполнения задания IV берутся новые, а не те, с которыми работали учащиеся при выполнении задания III.
Урок обобщения знаний(IX класс).
Тема урока. Геометрические фигуры и геометрические тела, периметр, площадь, поверхность, объем.
Цель урока. Обобщить знания учащихся о геометрических фигурах и телах, о способах вычисления периметров и площадей геометрических фигур, площадей поверхностей и объемов геометрических тел.
Оборудование. Модели геометрических фигур и тел, таблицы мер длины, площади, объема, таблички с формулами.
Ход урока.
I. Учитель сообщает тему урока, просит назвать известные учащимся геометрические тела, затем геометрические фигуры, сказать, что у них общего и чем они отличаются.
.2. Вызванный к доске ученик размещает на наборном полотне
модели геометрических фигур, которые он берет со стола учителя
(на столе модели геометрических фигур и тел).
3. Учитель вызывает к доске следующего ученика и просит показать границу некоторых геометрических фигур. Обращаясь к классу, задает вопросы: «Как назвать замкнутые линии, которые были показаны учеником? (Ломаные.) Чем является такая линия для геометрической фигуры? (Границей.) Какими мерами измеряется? (Мерами длины.) Как вычислить длину границы? (Измерить длину каждой стороны, полученные числа сложить.) Если измерить длины сторон многоугольника (показывает) и вычислить их сумму, то как будет называться полученная сумма? (Периметр.) Что называется периметром многоугольника? Как он вычисляется? Какими мерами выражается?
4. Ученики в тетрадях записывают тему урока, ниже слово «Периметр» и вычисляют (самостоятельно) периметр квадрата со стороной 4 см, прямоугольника со сторонами 1 дм и 3 см (предварительно длины сторон выражают в одинаковых мерах), равностороннего треугольника со стороной 15 мм.
5. Учитель показывает круг, спрашивает, как называется его граница.
6. Учитель просит учащихся сказать, какую еще известную для них величину они могут вычислить (показывает квадрат, прямоугольник, треугольник, круг). Учащиеся отвечают, что они умеют вычислять площади этих фигур.
7. В тетрадях дети пишут слово площадь и вычисляют площадь квадрата со стороной 6 см, прямоугольника со сторонами 5 см и 20 мм.
8. Учитель подводит итог проделанной работе: «Что вычисляли? (Периметр многоугольника, площадь многоугольника.) Какими мерами измеряется периметр (площадь)? Почему?»
9. Учитель указывает на геометрические тела, показывает их поверхности, спрашивает, что он показал. «Площади поверхности каких геометрических тел,— задает вопрос учитель,— вы умеете вычислять?»
Учитель выясняет, какими мерами измеряется площадь боковой и полной поверхности куба, любого прямоугольного параллелепипеда.
10. В тетрадях учащиеся записывают: «Площадь боковой, полной поверхности геометрического тела» — и вычисляют площади боковой полной поверхности куба с ребром 10 см, прямоугольного параллелепипеда с длиной ребер 2 см, 4 см, 3 см.
11. В тетрадях записывается: «Объем куба и прямоугольного параллелепипеда». Школьникам предлагается решить задачи на вычисление объема прямоугольного параллелепипеда с длиной ребер 5 см, 4 см, 6 см и куба с ребром 25 мм.
Результаты вычисления площади полной поверхности и объема соответствующих тел сравниваются.
12. Учитель просит вычислить длину багета, израсходованного
на рамку для картины, площадь оконного стекла, объем коробки,
имеющей форму прямоугольного параллелепипеда. Работа выполняется коллективно, поэтому учитель обсуждает с учащимися ход е выполнения.
13. Учитель вывешивает таблицы линейных мер, мер площади мер объема и спрашивает, в каких случаях результаты измерений выражаются этими мерами, повторяет с учащимися соотношение мер.
14. Под руководством учителя решается несколько примеров на все арифметические действия со значениями величин, выраженными мерами длины, площади, объема. Например:
6 км 98 м + 87 км 935 м
50 м — 9 м 8 см
6 дм2 7 см2*12
4 м3 20 дм3:5.
Затем детям предлагается выполнить самостоятельную работу, в которой встречаются примеры на все арифметические действия с числами, выраженными мерами длины, площади, объема.
15. Подводится итог работы на уроке. Учитель просит учеников назвать фигуры, периметр и площадь которых они умеют вычислять; геометрические тела. Учащиеся должны сказать, какими мерами выражаются периметр, площадь поверхности, объем.
16. Учитель оценивает работу учащихся на уроке, задает задание на дом.
Приводим примерный план урока (IX класс).
Тема урока. Геометрические тела, их свойства.
Цель урока. Повторить свойства куба и любого прямоугольного параллелепипеда, познакомить с цилиндром, пирамидой, конусом, шаром (узнавание, называние), закрепить различие геометрического тела и фигуры.
Оборудование. Набор моделей геометрических фигур и тел. Предметы, имеющие форму цилиндра, конуса, пирамиды, шара. Чертежи.
План урока.
1) Повторение свойств геометрических тел: прямоугольного параллелепипеда, его частного вида — куба.
2) Сравнение геометрических тел — куба и параллелепипеда — С геометрическими фигурами — квадратом и прямоугольником любого вида (повторение).
3) Знакомство с цилиндром, пирамидой, конусом, их элементами.
4)'Рассмотрение шара. Сечение шара. Центр и радиус шара.
5) Выделение предметов, имеющих форму геометрических тел, С которыми учащиеся познакомились. \
6) Сопоставление понятий: геометрическая фигура и геометрическое тело.
7) Вычерчивание геометрических фигур по данным размерам (прямоугольника, квадрата, круга, треугольника) и лепка геометрических тел (прямоугольного параллелепипеда, куба, шара, цилиндра, конуса, пирамиды).
8) Подведение итогов урока.
9) Задание на дом.
Домашнее задание по геометрии
Домашнее задание по геометрии может включать следующие виды работ: вычерчивание геометрических фигур, разверток геометрических тел, изготовление моделей, выполнение измерений (отрезков, углов и др.), решение задач с геометрическим содержанием (вычисление длины ломаной линии, периметра, площади, объема и т. д.). Закрепление знаний свойств геометрических фигур, геометрической терминологии.
В домашнем задании повторяются те виды работ, которыми дети занимались на уроке- геометрии.
Если дети изучают на уроке способы решения задач с геометрическим содержанием, то и домашнее задание должно содержать похожие задачи.
В старших классах вспомогательной школы урок геометрии проводится один раз в неделю. Это создает трудности в подготовке учащимися домашнего задания по геометрии. Дети забывают, какие вопросы они изучали на прошлом уроке, проверка домашнего задания отодвигается на долгий срок. Часто школьники работают над домашним заданием не сразу после урока геометрии, а накануне следующего урока, уже забыв все установки учителя. Поэтому на уроке при проверке выполнения учащимися домашнего задания учителю приходится тратить много времени на то, чтобы напомнить ученикам содержание предыдущего занятия.
В связи с этим домашнее задание по геометрии целесообразно задавать и проверять не один раз в неделю, а на каждом уроке математики. Если учитель будет включать в домашнее задание геометрический материал систематически (каждый или почти каждый день), он предупредит забывание школьниками изучаемых вопросов, сделает домашние задания более разнообразными по содержанию (арифметический материал будет сочетаться с геометрическим). Учитель получит возможность постепенно, небольшими «порциями» подготавливать карточки с геометрическим содержанием для домашних работ. (Например, для формирования навыков, определения вида углов — карточки с различными углами, для построения квадратов, любых прямоугольников с данными сторонами — карточки с отрезками различной длины и т. д.)
В течение недели учитель сможет дать учащимся различные варианты работ на закрепление того или иного понятия, формирование чертежного навыка и т. д. Например, если на уроке геометрии изучались параллельные прямые, то учитель в течение недели дает ученикам задания вычерчивать параллельные прямые (отрезки прямых) с разным расстоянием между двумя, тремя, четырьмя прямыми. Параллельные прямые вычерчиваются в разных положениях, вычерчиваются геометрические фигуры с параллельными сторонами и т. д.
При проверке домашнего задания учащиеся рассказывают о выполненной работе, получают установку на выполнение следующего задания.
При такой системе заданий на дом геометрический материал систематически повторяется и малыми дозами включается в уроки математики.
Перед учителем ставится задача увязывать по возможности геометрический материал с арифметическим.
Тетрадь по геометрии
В младших классах специальная тетрадь по геометрии не заводится. Все работы выполняются в тетрадях по математике (обводка, вычерчивание многоугольников по заданным их вершинам, раскрашивание, вычерчивание фигур по заданным размерам и т. д.). Для формирования навыков точности измерения и построения фигур, для выработки навыков работы с измерительными инструментами целесообразно проводить работу на нелинованной бумаге — такие листы могут быть вклеены или вложены в обычную тетрадь по математике.
В старших классах учащиеся могут иметь специальную тетрадь по геометрии в клеточку, но в нее необходимо вклеить листы нелинованной бумаги — для выполнения работ на построение фигур с заданными размерами.
Каждая работа датируется. В тетрадях записывается тема урока. Поля в тетрадях по геометрии не проводятся. Все чертежные работы выполняются карандашом, все надписи делаются чернилами. Каждая работа проверяется и оценивается учителем. В тетрадях учащиеся выполняют чертежи, решают задачи геометрического содержания.
Многие учителя вспомогательной школы на уроках геометрии все чертежные работы предлагают учащимся выполнять не в тетрадях, а на отдельных нелинованных листах бумаги.
Целесообразно для каждого ученика завести папку с этими листами нелинованной бумаги. Умение вычерчивать фигуры на такой бумаге приходит не сразу. У детей нужно воспитывать бережное, аккуратное отношение к работе с тем, чтобы чертежи получались более точными. Кроме того, следует приучать учеников к эстетическому оформлению чертежей. Отдельные листы бумаги более удобны для работы, так как ученикам легче обмениваться на уроках работами при осуществлении взаимопроверки (отдельный испорченный лист легко заменить новым).
Если на уроке или дома учащимся необходимо произвести вычисления при решении задачи геометрического содержания, то такие вычисления вносятся в обычную тетрадь по математике.
При выполнении чертежно-графических и измерительных работ v учащихся необходимо воспитывать:
I) Умение оформить лист, на котором выполняются чертежи. Сверху проводится прямая линия, над которой ученик записывает фамилию, имя, класс, число.
2) Умение разместить правильно, красиво, симметрично относительно краев листа и его центра чертеж.
3) Умение выполнить чертеж по заданным размерам с точностью до 1—2 мм при вычерчивании отрезков или элементов фигур и до 1—2° при построении углов фигур.
4) Умение оформить чертеж, обозначив его буквами.
|
Знать обозначения буквами точек, вершин, прямых, отрезков, ломаной, диаметра, радиуса, периметра, площади, объема.
УЧЕТ И КОНТРОЛЬ ЗНАНИЙ,
Глава 2
ТОЧКА. ЛИНИИ
Отрезок. Луч
В Iклассе учащиеся знакомятся с отрезком. На доске изображаются две точки и соединяются с помощью линейки. «Две точки и часть прямой между ними образуют отрезок,— сообщает учитель.— Эти две точки — концы отрезка». Чтобы учащимся было легче вспомнить термин «отрезок», можно натянуть нить (это «прямая») и «отрезать часть прямой» (оставляя нить натянутой).
Учащиеся должны научиться отмечать на прямой две точки и показывать отрезок (проводя карандашом от одной точки до другой). Отрезок можно выделить на прямой цветным карандашом.
Ребята учатся сравнивать отрезки (полоски бумаги, ленты, отрезки бечевки, тесьмы и др.), используя приемы наложения или приложения, например: «Одна полоска длиннее, а другая короче», «Синяя шита короче, чем красная, а красная лента длиннее, чем синяя». Мри сравнении учащиеся знакомятся с относительностью этих понятий. Они в конечном итоге должны понять, что о длине предмета мы можем судить, только сравнивая его с длиной других предметов, один и тот же предмет может быть длинным по отношению к дру-
гому, но коротким по отношению к третьему. Одновременно учитель добивается от детей правильного словесного оформления своих практических действий. Используя вышеизложенный пример, словесное оформление может быть таким: «Одна полоска длинная, а другая короткая», «Красная полоска длиннее, чем синяя. Синяя полоска короче, чем красная. Красная и зеленая полоски равные (одинаковые) по длине».
Ученики показывают отрезки на окружающих предметах. Учитель показывает, как ставить точки и соединять их, т. е. чертить отрезок. Учащиеся знакомятся с вычерчиванием линий, имеющих начало в данной точке. Без помощи линейки получается кривая линия. Если из точки проводим прямую, т. е. ограничиваем ее с одной стороны точкой, то получаем луч. Луч рассматривается как часть прямой. Если изобразить прямую, на ней точку, то получаются два луча. Луч имеет начало, но не имеет конца. Учащиеся чертят несколько лучей, исходящих из одной точки.
Следует проводить упражнения на дифференциацию точки, прямой, отрезка, луча. Сначала это целесообразно сделать на известных учащимся моделях, а затем на новых. Например, натянутая нить, бечевка, проволока — это прямые линии. Их можно продолжить в обе стороны. От нити, проволоки, бечевки отрезать часть, сделать «узелки» с двух сторон. Это отрезки. Их нельзя продолжить.
В III классе учащиеся знакомятся с точкой пересечения отрезков, линий. Точки пересечения следует показать учащимся на моделях линий и отрезков. Например, две проволоки, две нити (бечевки) пересекаются в одной точке. На листе бумаги (доске) чертим две пересекающиеся линии (отрезки), отмечаем точку пересечения. Учащиеся в тетрадях чертят пересекающиеся прямые, кривые линии, отрезки и отмечают их точки, их пересечения.
Ломаная линия
В IV классе учащиеся знакомятся с ломаной линией.
Чтобы они лучше запомнили термин ломаная линия, можно взять палочку и переломить ее 1—2 раза или сложить несколько раз узкую полоску бумаги — получили ломаную линию. Ломаная линия состоит из двух или большего количества отрезков, расположенных так, что конец одного отрезка служит началом другого. Удобно показать ломаную, согнув в нескольких местах проволоку или раздвинув складной метр. Затем следует показать ломаную линию на чертеже. Элементами ломаной линии являются отрезки и вершины, углы. Отрезки,
из которых состоит ломаная линия, могут иметь различную длину и положение.
Для сознательного усвоения признаков ломаной линии можно предложить учащимся работу с таблицами, например с таблицей, на которой изображена ломаная линия из пяти отрезков и пять отдельных отрезков, которые равны звеньям ломаной линии и имеют те же положения на плоскости. Закрывая на таблице все звенья ломаной, кроме одного, учитель показывает детям, что ломаная состоит из отрезков. Они пересчитывают отрезки. После этого учитель обращает внимание учеников на пять отдельных отрезков, расположенных в том же положении, что и отрезки ломаной линии. Дети пересчитывают их. Отрезков тоже пять. Количество отрезков одинаковое, и если отрезки ломаной и данные отрезки соответственно равны по длине, то длина ломаной и сумма длин отдельных отрезков равны. Учитель просит определить сходство и различие между ломаной линией из пяти отрезков и пятью отрезками.
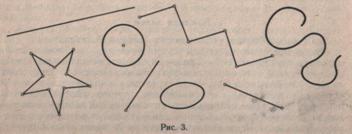
После знакомства с ломаной линией ученикам предлагаются задания на дифференциацию известных им линий. На таблицах (рис. 3), на доске, на поверхности окружающих предметов учащиеся выделяют и называют линии. Разного вида линии вычерчиваются в тетрадях.
В IV классе учащиеся знакомятся с замкнутыми и незамкнутыми линиями. Незамкнутая ломаная линия имеет начало и конец (так же как отрезок прямой), замкнутая не имеет ни начала, ни конца. Учитель сообщает учащимся, что если соединить начало и конец незамкнутой ломаной линии отрезком, то получится замкнутая ломаная линия. Если дана замкнутая ломаная линия, то достаточно отбросить один отрезок, чтобы она стала незамкнутой.
Учащиеся приводят примеры замкнутых и незамкнутых линий на окружающих их предметах.
Особое внимание следует уделить изучению многоугольников. На моделях и чертежах границы многоугольников выделяются цветом. Учащиеся убеждаются, что границы многоугольников — это замкнутые ломаные линии. Поэтому уместно проводить работу по определению числа отрезков в ломаных линиях, по конструированию ломаных линий из палочек, меняя вид линий и количество от-
|
резкое, из которых они состоят. Полезно ставить вопросы, развивающие пространственное воображение учащихся, например: «Представьте себе треугольник. Какая фигура образуется, если убрать одну сторону? Как нужно изменить чертеж треугольника, чтобы из треугольника получить четырехугольник?» И т. д.
Параллельно с замкнутыми, незамкнутыми ломаными учитель знакомит школьников с замкнутыми, незамкнутыми кривыми линиями.
Необходимо проводить упражнения на дифференциацию замкнутых и незамкнутых ломаных и кривых линий. Например, окружность, овал — кривые замкнутые линии, границы многоугольников — ломаные замкнутые линии, дуга — незамкнутая кривая линия.
Для вычерчивания кривых целесообразно пользоваться чертежными лекалами, которые могут быть изготовлены в школьных мастерских.
В V классе впервые вводится буквенное обозначение отрезков, ломаных линий и многоугольников. Для этого отбираются те латинские буквы, которые пишутся и произносятся одинаково с буквами русского алфавита (A, D, О, М, К, Е), а также буквы В, С, S, Р, К, V.
Действия с отрезками
На уроках математики учащиеся решают арифметические задачи на сложение, вычитание, увеличение, уменьшение длин отрезков. Решение задач иллюстрируется чертежами.
1) Чертежи отрезков даются на карточках, дети должны измерить отрезки и произвести нужное арифметическое действие с числами.
2) Учитель сообщает детям размеры отрезков. Отрезки ученики вычерчивают в тетрадях в качестве иллюстрации к решению задачи.
3) Требуется сложить два отрезка, данные на чертеже. Учащиеся измеряют их, складывают полученные при измерении числа и строят отрезок, равный сумме.
Далее надо показать, что действия могут выполняться не только с длинами отрезков, но и с самими отрезками. Перед изучением сложения отрезков геометрическим способом следует показать учащимся, как из двух кусков рейки можно получить одну рейку, если эти куски приложить концами друг к другу. Учащиеся должны понять, что полученная рейка является суммой двух данных.
Сложение отрезковгеометрическим способом состоит в следующем: на индивидуальных карточках задаются отрезки (два, три), и изображенные разным цветом, например один отрезок красного цвета, второй — зеленого, третий — синего. Учащиеся проводят произвольную прямую линию, отмечают точку и с помощью циркуля перенося г на нее первый отрезок, от конца первого отрезка откладывают второй отрезок, а от конца второго — третий отрезок. Отрезки чертят цветными карандашами, цвет их должен соответствовать цвету заданных отрезков. Построенный отрезок должен быть равен сумме данных отрезков. Проверкой может служить арифметический способ сложения длин отрезков.
Вначале даются одинаковые отрезки для всех учащихся, чтобы они смогли убедиться, что в результате сложения у всех получается одинаковый отрезок — сумма (проверка осуществляется с помощью измерителя).
Когда ученики овладевают приемом сложения отрезков, зада-
ния надо сделать более разнообразными. Например, найти сумму отрезков ломаной линии, сумму сторон треугольника, квадрата и друг<