Основные правила нанесения размеров на чертеже
(ГОСТ 2.307)
1. Линейные размеры на чертежах указывают в миллиметрах над размерной линией, но обозначение единицы измерения не наносят; размеры стрелок приведены на рис. 20а.
2. Общее количество размеров на чертеже должно быть наименьшим, но достаточным для изготовления и контроля изделия;
3. Размерные линии проводятся на расстоянии 10 мм от контура детали и не менее 7 мм друг относительно друга;
4. Выносные линии выходят за концы строк, которыми заканчиваются размерные линии, на 2-3 мм;
5. Над размерной линией, ближе к ее середине, наносят размерное число;
6. Если на чертеже несколько размерных линий, параллельных друг другу, то ближе к изображению наносят наименьший размер; (рис.8б)
7. Размерные линии не пересекаются никакими линиями;
8. Для обозначения диаметра пред размерным числом ставят знак Ф (рис.8в)
9. Для обозначения радиуса перед размерным числом ставят R.;(рис.8ж)
10. Нанесение размеров дуги (рис. 8 з);
11. При параллельных размерных линиях размерные числа располагают в шахматном порядке (рис. 8 б);
12. Расположение размерных чисел при различных наклонах размерных линий (рис. 8г);
1 3. Нанесение угловых размеров (рис.8 д);
1 4. Указание размеров повторяющихся элементов (рис. 8 е);
1 5. Нанесение размеров при недостатке места (рис 8и).
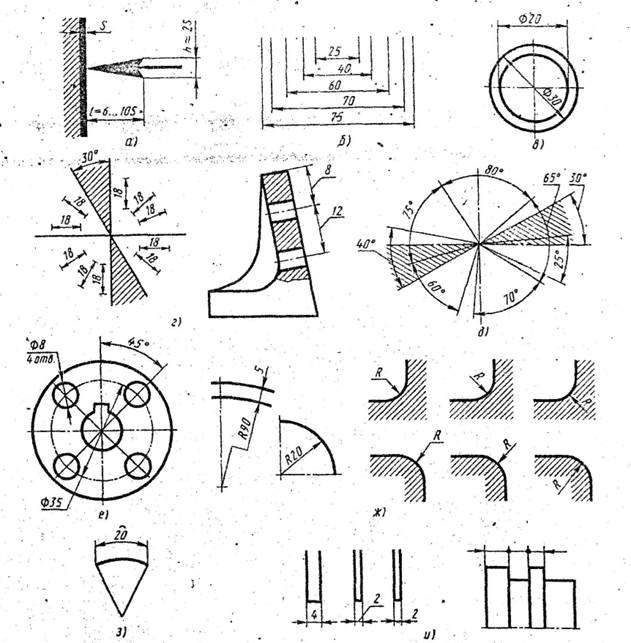
Рис.8
ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ (НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ)
ЭПЮР МОНЖА (КОМПЛЕКСНЫЙ ЧЕРТЕЖ).
ПРОЕЦИРОВАНИЕ ТОЧКИ
Начертательная геометрия изучает способы построения изображений пространственных фигур на плоскости и решения пространственных задач на чертеже.
Для изображения геометрических тел нужно уметь изображать их отдельные элементы: точки (вершины), прямые (ребра) , плоскости (грани).
Процесс получения изображений называется проецированием. Плоскость, на которую проецируют , называется плоскостью проекций.
Проецирование может быть центральным, когда проецирующие лучи выходят из одной точки (центра проецирования) и параллельным, когда проецирующие лучи параллельны друг другу. Если проецирующие лучи параллельны между собой и перпендикулярны плоскости проекций, - это прямоугольное проецирование, если пересекают плоскость проекций не под прямым углом – это косоугольное проецирование.
Прямоугольное проецирование на взаимно перпендикулярные плоскости проекций называется ортогональным проецированием, а полученные на них изображения- ортогональными проекциями.
Наиболее часто используют три взаимно перпендикулярные плоскости проекций: фронтальную V (вид спереди), горизонтальную H (вид сверху) и профильную W (вид слева) (на рисунках могут быть обозначены П1, П2, П3)
Линии пересечения плоскостей проекций называют осями координат и обозначаются Ох, Оу, Оz, точка их пересечения О- начало координат.
Если трехгранный угол с плоскостями проекций развернуть и совместить с плоскостью чертежа, полученные изображения называют эпюром Монжа.
Изображение на горизонтальной плоскости называется горизонтальной проекцией, на фронтальной- фронтальной проекцией, на профильной плоскости- профильной проекцией.
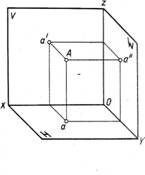
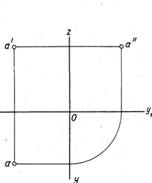 Построение эпюра точки. Положение точки в пространстве можно задать : 1) ее координатами x, y, z. Если через точку провести проецирующие лучи на плоскости проекций, получим три ее проекции; (рис.9)
Построение эпюра точки. Положение точки в пространстве можно задать : 1) ее координатами x, y, z. Если через точку провести проецирующие лучи на плоскости проекций, получим три ее проекции; (рис.9)
2) двумя ее проекциями. Тогда третью проекцию получаем, проводя линии проекционной связи от двух проекций на третью плоскость.
Рис. 9
МНОГОГРАННИКИ
Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником.
Призма
Призмойназывается многогранник, основаниями которого являются многоугольники, а боковыми гранями — четырехугольники (прямоугольники или параллелограммы).
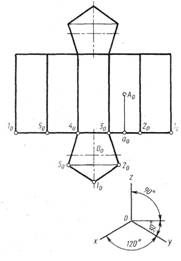
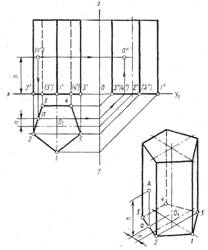 Построение ортогонального чертежа , точки на боковой поверхности и развертки призмы показано на рис. 10
Построение ортогонального чертежа , точки на боковой поверхности и развертки призмы показано на рис. 10

Пирамида
Пирамидой называется многогранник, в основании которого лежит многоугольник, а боковые грани являются треугольниками, имеющими общую вершину.
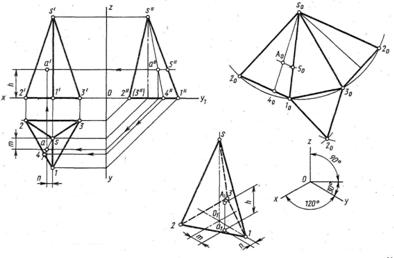 Рис.11 Рис.11 |
|
ТЕЛА ВРАЩЕНИЯ
Кривые поверхности образуются в результате перемещения подвижной линии по неподвижной кривой. Линия, по которой происходит перемещение, называется направляющей. Линия, которая перемещается, называется образующей.
Поверхности, которые образуются вращением образующей вокруг неподвижной оси, называются поверхностями вращения.
Цидиндр. Это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями. Направляющая- окружность; образующая движется параллельно самой себе вдоль этой окружности. Если ось цилиндра перпендикулярна его основанию, цилиндр называется прямым.
Ортогональный чертеж , построение точки на боковой поверхности и развертка показаны на рис 12. Длина развертки боковой поверхности равна 2πR.
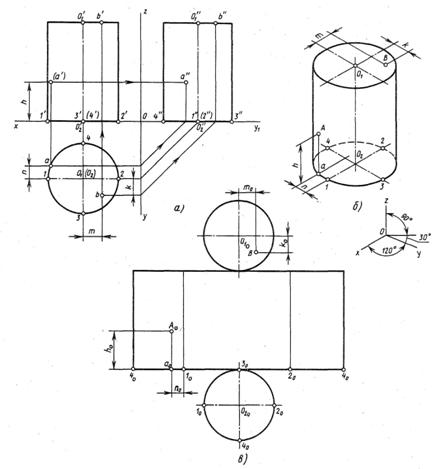
Рис.12
Конус.
Это геометрическое ело, ограниченное конической поверхностью и плоскостью. Коническая поверхность получается вращением вокруг оси прямой (образующей), которая пересекает эту ось в точке, называемой вершиной конуса.
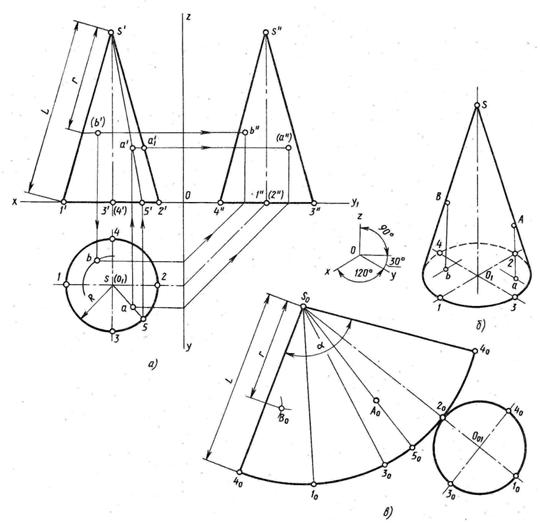 Рис.13 Рис.13 |
Полный прямой круговой конус изображен на рис. 13. Если отсечь верхнюю часть конуса, останется усеченный конус.
Ортогональный чертеж, построение точки на боковой поверхности и развертка показаны на рис. 12
Развертка: строится круговой сектор радиусом = длине образующей (L) с углом α=360˚R/L и пристраивается основание- окружность радиусом R.
Для построения аксонометрии тела вращения сначала строится аксонометрическая проекция основания. Затем из центра основания параллельно оси Z вверх откладывают его высоту .Для конуса: из полученной точки проводят касательные к овалу основания, для цилиндра- из полученной точки проводят аксонометрические оси , строят верхнее основание в аксонометрии и построенные овалы соединяют двумя касательными.
Пример нахождения проекций точек на поверхности геометрических тел показаны на рис.14. Для построения этих проекций используют линии связи .
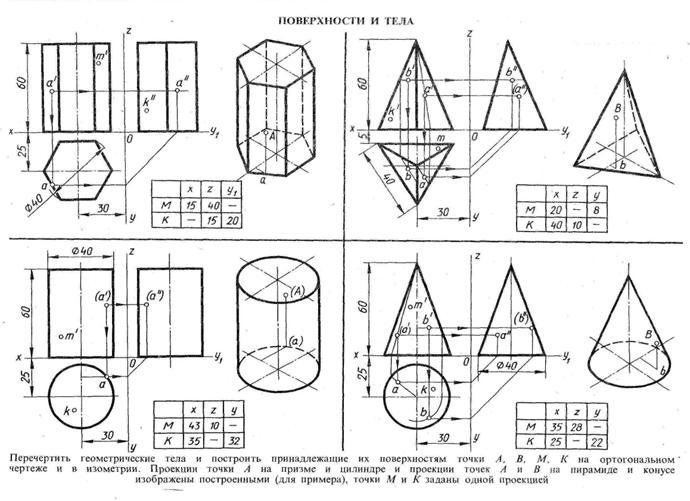 |
Рис.14
Пример построения в трех проекциях группы геометрических тел, взаимное расположение которых представлено на горизонтальной проекции и изометрической проекции представлен на рис.15.
Построение проводят в следующей последовательности: определяют по заданной изометрии вид каждого геометрического тела (конус, цилиндр, призма, пирамида), строят по заданным размерам горизонтальную проекцию группы в соответствии с рисунком задания. Затем проводят линии связи на фронтальную и профильную плоскость и откладывают высоту геометрических тел.
Обводят видимые контуры сплошной основной линией, невидимые- пунктирной.
Изометрию строят в такой последовательности: 1)Проводят аксонометрические оси под углом 120˚; 2)Находят координаты центров оснований всех тел- замеряют на виде сверху и откладывают эти расстояния без искажения параллельно аксонометрическим осям х и у; 3)Проводят из центров вертикальные оси, на которых откладывают высоту каждого тела; 4) Строят в тонких линях тела;
5)Обводят сплошной основной линией все видимые, пунктиром - невидимые линии.
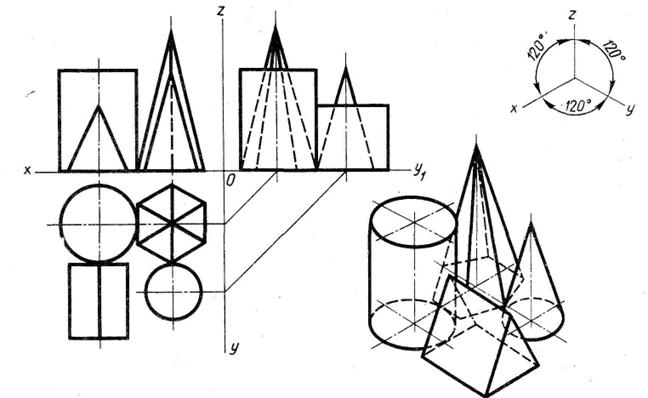 |

