Разработал преподаватель Краснова Л.Г.
Утверждаю
Зам. директора по УР
_________И.Н. Матяшова
« »_______________2017год.
Инженерная графика
МЕТОДИЧЕСКОЕ РУКОВОДСТВО
по выполнению графических работ
раздела
«Геометрическое и проекционное черчение»
(1 семестр)
для студентов очного отделения
специальности 23.02.03
(индивидуальное обучение)
Разработал преподаватель Краснова Л.Г.
Красноармейск
2017г.
Содержание
Общие требования к выполнению работы………………………………………3
1.Геометрические построения
1.1.Построение уклонов и конусности ....................…………………………….4
1.2.Деление окружности на равные части ………………………………………5
1.3.Построение сопряжений ……………………………………………………...6
2.Основные правила нанесения размеров на чертеже ………………………….8
3.Проекционное черчение (начертательная геометрия)
3.1.Эпюр Монжа (комплексный чертеж). Проецирование точки …………… 10
3.2.Многогранники ………………………………………………………………11
3.3.Тела вращения ………………………………………………………………..12
3.4.Построение аксонометрических проекций (изометрии) плоских фигур….15
3.5.Сечение тел вращения плоскостями ………………………………………...17
3.6.Сечение многогранников плоскостями ……………………………………..18
3.7.Пересечение тел вращения …………………………………………………..19
3.8.Пересечение многогранников ……………………………………………….20
3.9.Список литературы……………………………………………………………21
4.Варианты заданий………………………………………………………………22
Общие требования к выполнению графических работ
Графические работы выполняются на листах ватмана формата А3 с основной надписью по форме 1 ГОСТ 2.104-68. Все чертежи выполняются простым карандашом с помощью чертежных инструментов. В задачах по начертательной геометрии для наглядности допускается линии пересечения поверхностей тел выделять красным карандашом (пастой), а сами поверхности растушевывать бледными цветными карандашами.
Все вспомогательные построения, линии проекционной связи выполняются бледными тонкими линиями и сохраняются.
Основная надпись заполняется карандашом стандартным чертежным шрифтом №5- №7.
Шифр чертежа: ИГ 23.02.03 16 № варианта № задачи
Наименование чертежа – название задачи (например: Геометрические построения).
Графическая работа 1. Геометрические построения
Выполнить изображения контуров деталей и нанести размеры в соответствии с вариантом. На деталях с уклоном и конусностью проставить размер уклона и конусности, предварительно рассчитав размеры, обозначенные *.. Все детали расположить на одном листе формата А3.
(Темы: «Уклон и конусность», «Сопряжения», «Деление окружности на части», «Нанесение размеров»).
Графическая работа 2. Точки на поверхности геометрических телПостроить третью проекцию геометрических тел. Найти проекции точек, находящихся на их поверхности.(Темы: «Поверхности и тела», «Проекции точек на поверхности геометрических тел»)
Графическая работа 3
Задача 3.1. Сечение геометрических тел вращения плоскостями(лист №1)
Выполнить чертеж усеченного цилиндра. Найти действительную величину фигуры сечения. Построить аксонометрическую проекцию усеченного тела.
Задача 3.2 Сечение многогранников плоскостями (лист №2)
Выполнить чертеж усеченной пирамиды. Найти действительную величину фигуры сечения. Построить аксонометрическую проекцию усеченного тела.
(Темы: «Сечение геометрических тел плоскостями», «Определение натуральной величины геометрической фигуры», «Способы преобразования чертежа»)
Графическая работа 4
Задача 4.1 Взаимное пересечение поверхностей тел вращения(лист №1)
Построить линии пересечения поверхностей цилиндров.
Задача 4.2 Взаимное пересечение поверхностей многогранников(лист №2)
Построить линии пересечения поверхностей цилиндров
Тема: «Построение линии пересечения поверхностей тел с помощью вспомогательных секущих плоскостей».
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ.
Рис.2
Конусность (рис.3)
Конусностью называется отношение диаметра D основания прямого кругового конуса к его высоте Н.
Для усеченного конуса конусность выражается отношением разности диаметров D и d нормальных сечений кругового конуса к расстоянию между ними . Обозначение конусности наносится на линии-выноске со стрелкой. Перед размерным числом, характеризующим конусность, наносят знак, острый угол которого должен быть направлен в сторону вершины конуса. (рис.3 )


Рис.3
Рис.4
1.2.6. Деление на 7 равных частей (рис.4 е).
Приняв за центр один из концов диаметра (точку С), проведите дугу радиусом 20 мм до пересечения с окружностью. Точки пересечения соедините отрезком прямой . Половина этого отрезка (EF) примерно равна стороне вписанного семиугольника. Радиусом FE сделайте поочередно 7 засечек на окружности, начав с точки С. Полученные 7 точек соедините.
1.2.7.Деление на 5 равных частей (рис.4 ж).
Приняв за центр один из концов диаметра (точку В), проведите дугу радиусом 20мм до пересечения с окружностью и точки пересечения соедините прямой. Приняв за центр точку пересечения прямой с :горизонтальным диаметром (точку Е), проведите дугу через точку С до пересечения с этим диаметром. Точку пересечения F соедините с точкой С. Отрезок СF будет примерно равен стороне вписанного пятиугольника ; ОF - стороне вписанного десятиугольника. Радиусом СF поочередно сделайте 5 засечек на окружности, начиная с точки С. Полученные 5 точек соедините.
1.2.8.Деление на 10 равных частей (рис.4з).
Радиусом ОF сделайте поочередно 10 засечек на окружности, полученные точки соедините.
СОПРЯЖЕНИЯ
1.3.1.Сопряжение двух прямых (рис.5.)
Даны две параллельные прямые АВ и СD (рис 5 в) , задан размер EF .Разделите отрезок EF пополам, и из точки О проведите дугу радиусом R=EF/2, соединяя точки Е и F
 Рис5 Рис5 |
1.3.2.Сопряжения углов (рис.5 а, б).
Даны две прямые , пересекающиеся под углом ( прямым, острым или тупым), и радиус сопряжения Е..
Проведите по два перпендикуляра к двум сторонам углаи отложите на них отрезки ,равные R.. Через полученные точки проведите прямые параллельно сторонам угла.. О - точка пересечения этих двух прямых -есть центр сопряжения. Из точки О опустите перпендикуляры на стороны угла. Точки пересечения перпендикуляров и сторон угла соедините дугой радиусом R с центром в точке О.
1.3.3.Сопряжение прямой сокружностью (рис.6а.) Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите прямую, параллельную заданной , на расстоянии R1. Из центра окружности О радиусом R2= R + R1 сделайте на прямой засечку О1 . Через О и О1 проведите прямую, получите на окружности точку К. Из точки О1 проведите О1К1 перпендикулярно заданной прямой. Из центра сопряжения О1 проведите дугу радиусом R1, соединяя точки К1 и К. Это внешнее сопряжение
 Рис.6 Рис.6 |
Внутреннее сопряжение. (рис.6 б).
Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите построение аналогично предыдущему, учитывая , что в данном случае
R2 = R-R1
1.3.4.Сопряжение двух окружностей.
Внешнее сопряжение (рис.7а).
Даны две окружности радиусом R1, и R2 и радиус сопряжения R.
 Рис.7 Рис.7 |
Проведите дуги из центра О1 радиусом R.+ R 1 , из О2 - радиусом R.+ R 2. Точка их пересечения О3 -центр сопряжения.
Внутреннее сопряжение(рис.7б)
Даны две окружности радиусом R1и R2 и радиус сопряжения R. Проведите дуги : из точки О1 радиусом R- R1, из точки О2 радиусом R-R2. Точка их пересечения О3 -центр сопряжения.
Смешанное сопряжение (рис.7 в).
Даны две окружности радиусом R1 и R2,ирадиус сопряжения R.
Проведите дуги : из центра О1 радиусом R.-R1, из центра О2 радиусом R+R2. Точка пересечения дуг О3- центр сопряжения.
Рис.8
ПРОЕЦИРОВАНИЕ ТОЧКИ
Начертательная геометрия изучает способы построения изображений пространственных фигур на плоскости и решения пространственных задач на чертеже.
Для изображения геометрических тел нужно уметь изображать их отдельные элементы: точки (вершины), прямые (ребра) , плоскости (грани).
Процесс получения изображений называется проецированием. Плоскость, на которую проецируют , называется плоскостью проекций.
Проецирование может быть центральным, когда проецирующие лучи выходят из одной точки (центра проецирования) и параллельным, когда проецирующие лучи параллельны друг другу. Если проецирующие лучи параллельны между собой и перпендикулярны плоскости проекций, - это прямоугольное проецирование, если пересекают плоскость проекций не под прямым углом – это косоугольное проецирование.
Прямоугольное проецирование на взаимно перпендикулярные плоскости проекций называется ортогональным проецированием, а полученные на них изображения- ортогональными проекциями.
Наиболее часто используют три взаимно перпендикулярные плоскости проекций: фронтальную V (вид спереди), горизонтальную H (вид сверху) и профильную W (вид слева) (на рисунках могут быть обозначены П1, П2, П3)
Линии пересечения плоскостей проекций называют осями координат и обозначаются Ох, Оу, Оz, точка их пересечения О- начало координат.
Если трехгранный угол с плоскостями проекций развернуть и совместить с плоскостью чертежа, полученные изображения называют эпюром Монжа.
Изображение на горизонтальной плоскости называется горизонтальной проекцией, на фронтальной- фронтальной проекцией, на профильной плоскости- профильной проекцией.
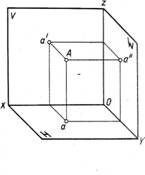
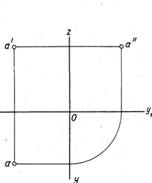 Построение эпюра точки. Положение точки в пространстве можно задать : 1) ее координатами x, y, z. Если через точку провести проецирующие лучи на плоскости проекций, получим три ее проекции; (рис.9)
Построение эпюра точки. Положение точки в пространстве можно задать : 1) ее координатами x, y, z. Если через точку провести проецирующие лучи на плоскости проекций, получим три ее проекции; (рис.9)
2) двумя ее проекциями. Тогда третью проекцию получаем, проводя линии проекционной связи от двух проекций на третью плоскость.
Рис. 9
МНОГОГРАННИКИ
Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником.
Призма
Призмойназывается многогранник, основаниями которого являются многоугольники, а боковыми гранями — четырехугольники (прямоугольники или параллелограммы).
 Построение ортогонального чертежа , точки на боковой поверхности и развертки призмы показано на рис. 10
Построение ортогонального чертежа , точки на боковой поверхности и развертки призмы показано на рис. 10

Пирамида
Пирамидой называется многогранник, в основании которого лежит многоугольник, а боковые грани являются треугольниками, имеющими общую вершину.
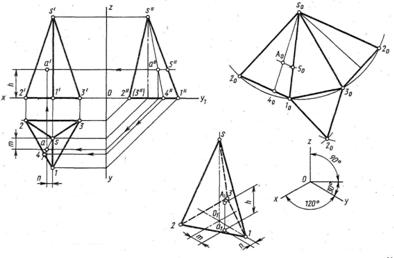 Рис.11 Рис.11 |
|
ТЕЛА ВРАЩЕНИЯ
Кривые поверхности образуются в результате перемещения подвижной линии по неподвижной кривой. Линия, по которой происходит перемещение, называется направляющей. Линия, которая перемещается, называется образующей.
Поверхности, которые образуются вращением образующей вокруг неподвижной оси, называются поверхностями вращения.
Цидиндр. Это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями. Направляющая- окружность; образующая движется параллельно самой себе вдоль этой окружности. Если ось цилиндра перпендикулярна его основанию, цилиндр называется прямым.
Ортогональный чертеж , построение точки на боковой поверхности и развертка показаны на рис 12. Длина развертки боковой поверхности равна 2πR.
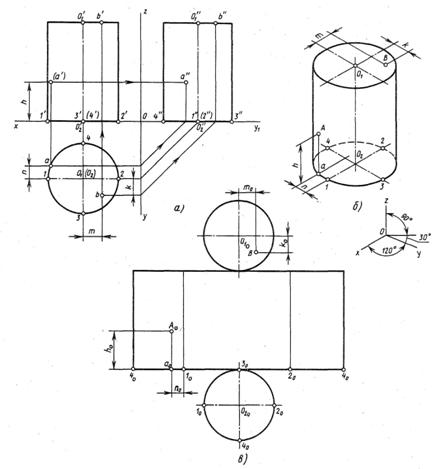
Рис.12
Конус.
Это геометрическое ело, ограниченное конической поверхностью и плоскостью. Коническая поверхность получается вращением вокруг оси прямой (образующей), которая пересекает эту ось в точке, называемой вершиной конуса.
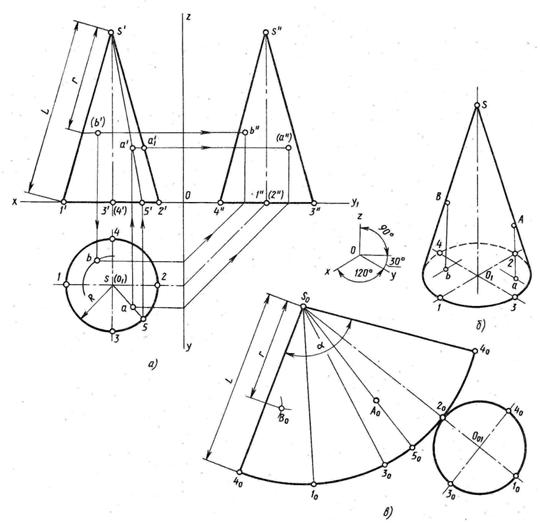 Рис.13 Рис.13 |
Полный прямой круговой конус изображен на рис. 13. Если отсечь верхнюю часть конуса, останется усеченный конус.
Ортогональный чертеж, построение точки на боковой поверхности и развертка показаны на рис. 12
Развертка: строится круговой сектор радиусом = длине образующей (L) с углом α=360˚R/L и пристраивается основание- окружность радиусом R.
Для построения аксонометрии тела вращения сначала строится аксонометрическая проекция основания. Затем из центра основания параллельно оси Z вверх откладывают его высоту .Для конуса: из полученной точки проводят касательные к овалу основания, для цилиндра- из полученной точки проводят аксонометрические оси , строят верхнее основание в аксонометрии и построенные овалы соединяют двумя касательными.
Пример нахождения проекций точек на поверхности геометрических тел показаны на рис.14. Для построения этих проекций используют линии связи .
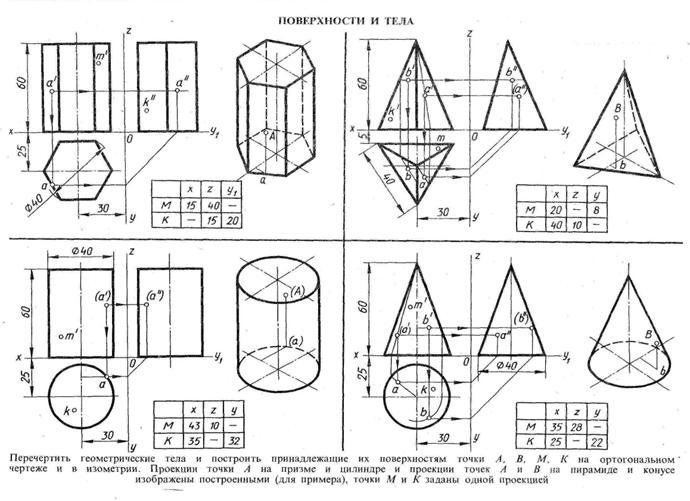 |
Рис.14
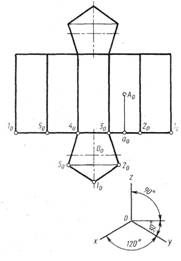
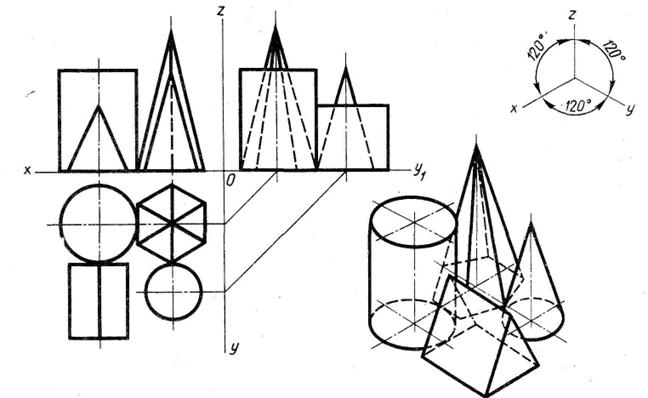
Пример построения в трех проекциях группы геометрических тел, взаимное расположение которых представлено на горизонтальной проекции и изометрической проекции представлен на рис.15.
Построение проводят в следующей последовательности: определяют по заданной изометрии вид каждого геометрического тела (конус, цилиндр, призма, пирамида), строят по заданным размерам горизонтальную проекцию группы в соответствии с рисунком задания. Затем проводят линии связи на фронтальную и профильную плоскость и откладывают высоту геометрических тел.
Обводят видимые контуры сплошной основной линией, невидимые- пунктирной.
Изометрию строят в такой последовательности: 1)Проводят аксонометрические оси под углом 120˚; 2)Находят координаты центров оснований всех тел- замеряют на виде сверху и откладывают эти расстояния без искажения параллельно аксонометрическим осям х и у; 3)Проводят из центров вертикальные оси, на которых откладывают высоту каждого тела; 4) Строят в тонких линях тела;
5)Обводят сплошной основной линией все видимые, пунктиром - невидимые линии.
 |

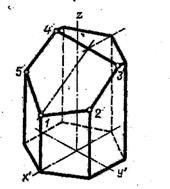
Окружность в изометрии (Рис.16)
Строят аксонометрические оси x′, y′, z′ под углом 120˚. Вычерчивают ромб АВСЕ, стороны которого равны диаметру заданной окружности D. Стороны ромба пересекли оси в точках 1,2,3,4. Из точек А и В, как из центров, радиусом А1=А3=В2=В4 проводят дуги, пересекающие большую диагональ АВ ромба в точках О1 и О2 (центрах малых дуг овала). Через точки О1 и О2 под углом 60˚ к большой диагонали АВ проводят прямые, пересекающие вертикальную ось в точках О2 и О4 и стороны ромба в точках М1, М2, М3, М. Затем из точек
О1 и О2 ,как из центров ,проводят малые дуги овала радиусом О1М=О2М2, а из точек О2 и О4 ,как из центров, проводят большие дуги радиусом О3М1=О4М2.
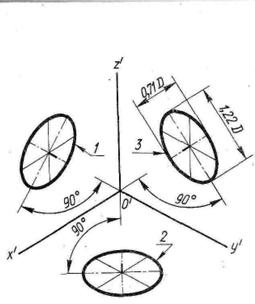
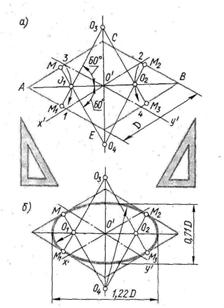
Рис.16
Правильный шестиугольник в изометрии (рис 17)
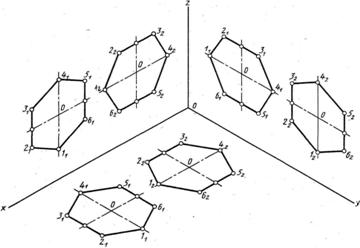
Рис.17.
Построение изометрии начинают с построения аксонометрических осей под углом 120˚. Размеры по осям и параллельные им откладывают без искажения, т.е. в натуральную величину.
Рис.18
2)Выбирают произвольно на линии пересечения точки 1,2,3,4,5,6,7 и с помощью линий связи находят их фронтальные и профильные проекции.
3)Строят натуральную величину фигуры сечения, используя метод перемены плоскостей проекций. Для этого на фронтальной плоскости проекций проводят осевую линию параллельно секущей плоскости. Из точек а′,1′,2′,3′,4′ проводят перпендикуляры к этой осевой линии и на них откладывают (симметрично осевой линии) размеры отрезков ab, 1-7, 2-6, 3-5, измеренные на виде сверху. Обводят полученные точки a1 ,11,21,31,41,51,61,71,b1 плавной кривой и получают натуральную величину фигуры сечения.
4)Построение аксонометрической проекции (изометрии) : строят оси под углом 120˚, на них проводят построение овала (окружности нижнего основания в изометрии). На ось x переносят точки с горизонтальной проекции, в которых отрезки ab, 1-7, 2-6, 3-5 пересекают горизонтальную ось окружности. Из этих точек восстанавливают перпендикуляры, на которых откладывают расстояния от точек а′,1′,2′,3′,4′ до оси x , измеренные на фронтальной плоскости проекций.
Через полученные точки проводят линии параллельно оси y , на которых откладывают соответственно отрезки ab, 1-7, 2-6, 3-5 . Обводят плавной кривой фигуру сечения. Если секущая плоскость пересекает верхнее основание цилиндра, достраивают верхнее основание, как часть окружности в изометрии (часть овала , параллельно такой же части нижнего основания). Если секущая плоскость не пересекает верхнее основание, фигура сечения представляет собой овал, построенный по точкам.
Рис.19
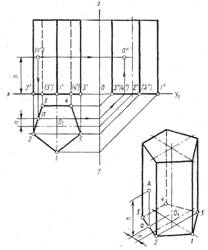
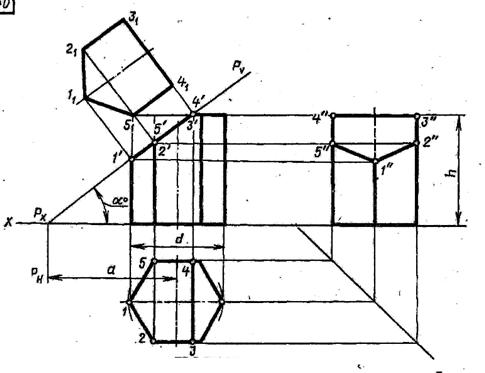
Последовательность построений.
1)Строят по заданным размерам три проекции пирамиды и на фронтальной плоскости проекций- секущую плоскость (PxPv). Отмечают точки пересечения ребер пирамиды с секущей плоскостью (точки 1′,2′,3′,4′). С помощью линий связи получают проекции этих точек на горизонтальной и профильной плоскости проекций. Соединяя полученные точки отрезками прямых, получают проекции фигуры сечения.
2)Натуральную величину фигуры сечения получают с помощью способа вращения: проводят дуги из центра (точки Px ) от точек 1′,2′,3′,4′ до пересечения с осью х. На пересечении соответствующих линий связи получают точки 11,21,31,41. Соединяя их отрезками , получают натуральную величину фигуры сечения.
3)Построение изометрии. Строят оси под углом 120˚. На осях x и y откладывают в натуральную величину диагонали основания пирамиды, а по оси z – высоту пирамиды. Соединяют полученные точки, получают неусеченную пирамиду. Для построения точек фигуры сечения на оси х откладывают отрезок 1-3, на оси y – отрезок 2-4. Из полученных точек проводят вверх линии параллельно оси z до пересечения с ребрами пирамиды. Точки пересечения соединяют, получают фигуру сечения. Обводят сплошной основной видимые контуры и пунктиром- невидимые.
ПЕРЕСЕЧЕНИЕ ТЕЛ ВРАЩЕНИЯ
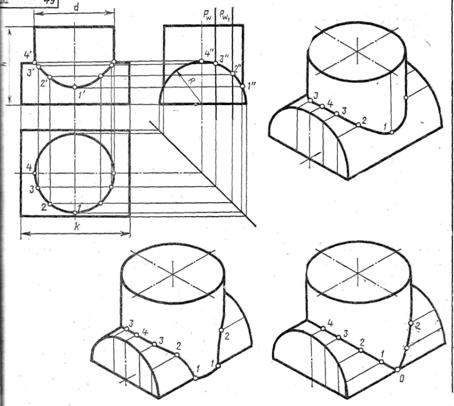
Рис.20
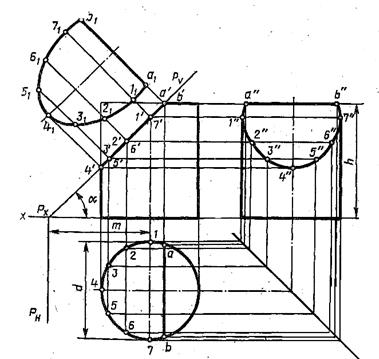
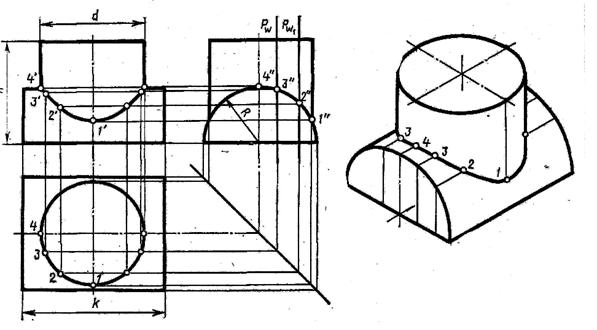
Последовательность построений.
1)Строят в тонких линиях три проекции пересекающихся цилиндров. На горизонтальной плоскости (виде сверху) отмечают произвольно несколько точек пересечения тел (они располагаются на окружности «стоящего» цилиндра) –точки 1,2,3,4. С помощью линий связи получают профильные проекции этих точек- 1˝,2˝,3˝,4˝. А проводя линии связи от профильной и горизонтальной проекции на фронтальную, получим точки 1′,2′,3′,4′. Соединяя эти точки плавными кривыми, получим линии пересечения тел.
В зависимости от размеров диаметров цилиндров линия пересечения будет иметь разный вид, как показано на объемных изображениях («стоящий» меньше «лежащего», «стоящий» больше «лежащего», оба диаметра одинаковы).
ПЕРЕСЕНИЕ МНОГОГРАННИКОВ
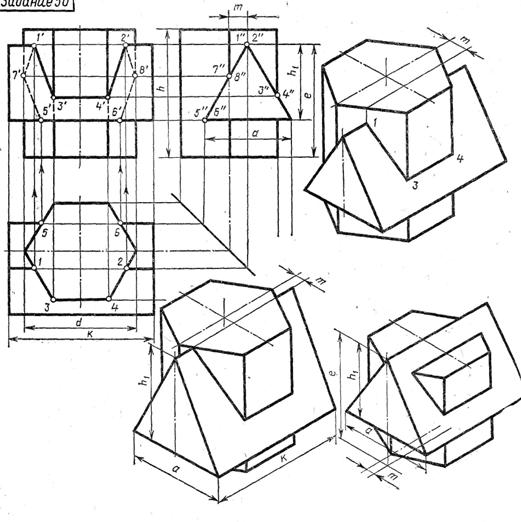
Рис.21
Последовательность построений.
1)Строят проекции пересекающихся призм в тонких линиях по заданным размерам.
2)На горизонтальной плоскости (виде сверху) отмечают характерные точки линии пересечения : 1,2,3,4,5,6,7,8. Проводя линии связи на профильную плоскость, получают точки 1˝=2˝,3˝=4˝,5˝=6˝,7˝=8˝.
3)Проводят линии связи от горизонтальных и профильных проекций точек на фронтальную плоскость. Пересечения линий связи дадут точки 1′,2′,3′,4′,5′,6′,7′,8′. Соединяя полученные точки, получают линию пересечения призм.
4)Видимые контуры обводят сплошной основной, невидимые- пунктирной линией. Точки, расположенные на передней грани треугольной призмы –видимые (1′,2′,3′,4′), на задней грани- невидимые (5′,6′,7′,8′).
ЭСКИЗ И ТЕХНИЧЕСКИЙ РИСУНОК МОДЕЛИ.
Эскиз- это чертеж в трех проекциях, выполненный от руки без масштаба, но с сохранением пропорций детали.
Технический рисунок- это наглядное изображение, аксонометрия, выполненная от руки.
Выполнение рисунка детали начинают с построения его габаритного очертания-«клетки», выполняемой «от руки» тонкими линиями (в данном случае - параллелепипед). Затем деталь мысленно расчленяют на отдельные геометрические элементы, постепенно зарисовывая все элементы (части) детали.
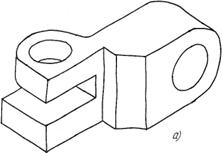
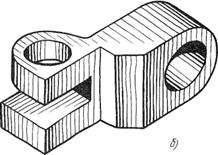
Рис. 22
Технические рисунки предмета получаются более наглядными, если их покрыть штрихами (рис.22, б). При нанесении штрихов считают, что лучи света падают на предмет справа и сверху или слева и сверху.
Освещенные поверхности штрихуют тонкими линиями на большом расстоянии друг от друга, а теневые —более толстыми линиями, располагая их чаще. Боковые поверхности пирамиды и конуса штрихуют линиями, проходящими через их вершину.(рис.72а-д)
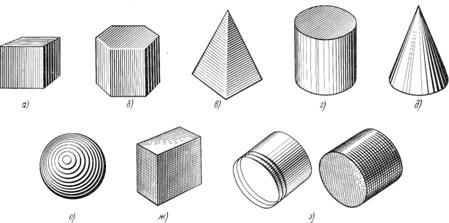
Рис. 23
На изображения сферических поверхностей и поверхностей вращения наносят криволинейные штрихи (части концентрических окружностей) разной толщины и с разными промежутками между штрихами.
Иногда изображения геометрических тел или деталей покрывают шраффировкой, которая представляет собой сложную штриховку, например, в виде сетки. Освещенные поверхности предмета покрывают тонкими линиями шраффировки. По мере приближения к затемненным местам эти линии утолщают. Кроме того, ближние к наблюдателю контурные линии предмета выполняют более толстыми, чем удаленные.
На рисунках деталей (см. рис.23 е-з)) применена подобная
штриховка.
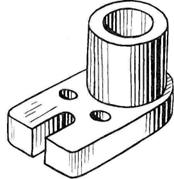
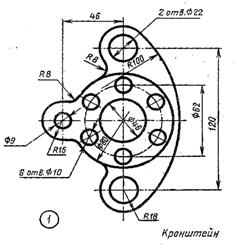
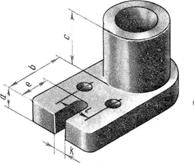 Зарисовывая деталь с натуры (например кронштейн, рис.24), надо не только внимательно рассмотреть форму, но и сравнить соответствие размеров отдельных элементов детали.. На рис.24 дан рисунок этой детали с учетом пропорций ее частей.
Зарисовывая деталь с натуры (например кронштейн, рис.24), надо не только внимательно рассмотреть форму, но и сравнить соответствие размеров отдельных элементов детали.. На рис.24 дан рисунок этой детали с учетом пропорций ее частей.
С помощью разрезов на рисунках и аксонометрических проекциях можно показать внутреннюю форму детали.
Приемы выполнения разрезов
Полые модели и детали выполняют в аксонометрии с разрезами. Это показано на рис. 25, где изображена деталь с отверстиями, в разрезе.
Если окружность неполная, то для ее изображения вычерчивают тонкой линией полный овал или эллипс, а затем обводят контурной линией нужную часть овала (рис. 25).
| Рис. 25 |
Список литературы
1. Р.С.Миронова, Б.Г.Миронов.Инженерная графика. М.:, Высшая школа.; Издательский центр «Академия», 2001. -288 с.
2. А.М.Бродский, Э.М.Фазлулин, В.А. Халдинов. Инженерная графика. М.: ИРПО: .; Издательский центр «Академия», 2003 – 400 с.
3. А.А. Чекмарев, В.К. Осипов. Справочник по черчению. М.: .; Издательский центр «Академия», 2005 – 336 с
4.В.П.Куликов. «Стандарты инженерной графики». М.:, «Форум»,2008- 240с
Варианты заданий
Графическая работа 1. Выполнить на формате А3 чертежи деталей с сопряжениями, уклоном и конусностью.
| 1 вариант | ||
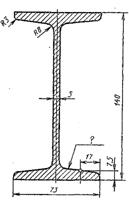
 | 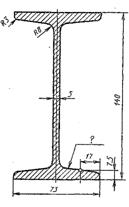 Для двутавра принять уклон 10%. Для двутавра принять уклон 10%. | 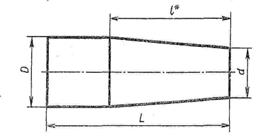 Размеры заглушки L=70 L=100 D=50 d=25 Конусность 1:3 Размеры заглушки L=70 L=100 D=50 d=25 Конусность 1:3 |
| 2 вариант | ||
 |  Для двутавра принять уклон 10%. Для двутавра принять уклон 10%. | Размеры пробки: L=105 D=30 d1=16 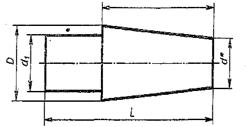 l=70 Конусность 1:3 l=70 Конусность 1:3 |
| 3 вариант | ||
 |  Для двутавра принять уклон 10%. Для двутавра принять уклон 10%. | 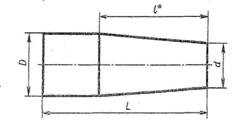 Размеры заглушки L=70 L=100 D=50 d=25 Конусность 1:3 Размеры заглушки L=70 L=100 D=50 d=25 Конусность 1:3 |
| 4 вариант | ||
 | Для двутавра принять уклон 10%.  | Размеры пробки: L=110 D=50 d1=25 l=75 Конусность 1:5 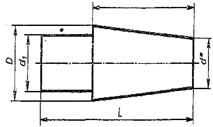 |
| 5 вариант | ||
 |  Для двутавра принять уклон 10%. Для двутавра принять уклон 10%. | Размеры втулки: L=100 D1=55 d=25l=75 Конусность 1:5 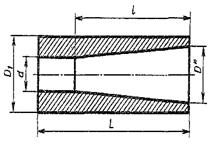 |
| 6 вариант | ||
 Для двутавра принять уклон 10%. Для двутавра принять уклон 10%. | Размеры пробки: L=110 D=50 d1=25 l=75 Конусность 1:5  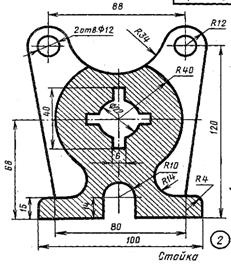 | |
| 7 вариант | ||
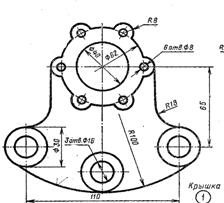 | Для стойки принять уклон 18%. 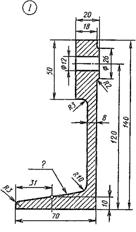 | Размеры втулки: L=100 D1=55 d=25l=75 Конусность 1:10 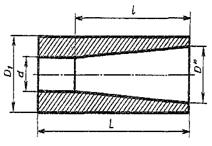 |
| 8 вариант | ||
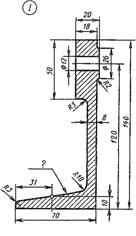
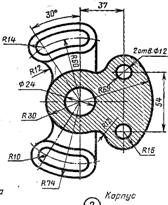 | Для стойки принять уклон 15%. 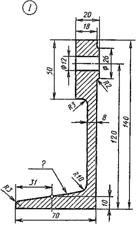 | 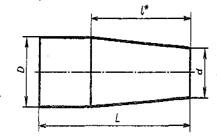 |
| 9 вариант | ||
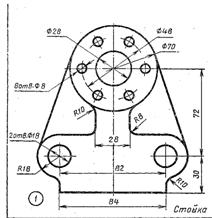 |  Для стойки принять уклон 10%. Для стойки принять уклон 10%. | Размеры пробки: L=100 D=50 d1=25 l=75 Конусность 1:7  |
| 10 вариант | ||
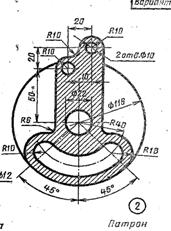 | Для стойки принять уклон 12%.  | Размеры заглушки: L=100 D=40 d=25 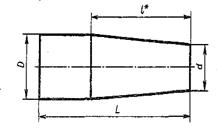 Конусность 1:5 Конусность 1:5 |
Графическая работа 2
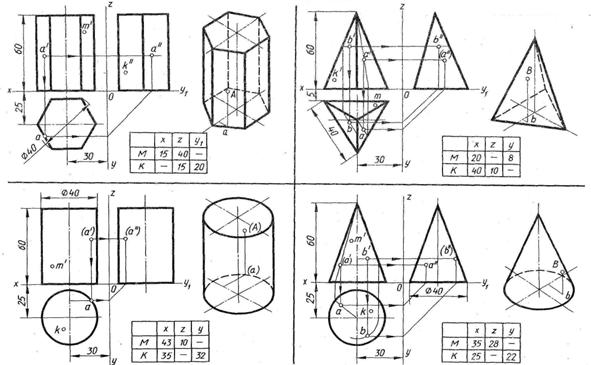 Перечертить геометрические тела и построить принадлежащие их поверхностям точки A,B,M,K на ортогональном чертеже и изометрии.
Перечертить геометрические тела и построить принадлежащие их поверхностям точки A,B,M,K на ортогональном чертеже и изометрии.
Графическая работа 3
| Обозначение | № варианта | |||||||||
| d | 60 | 58 | 54 | 62 | 60 | 58 | 54 | 62 | 60 | 58 |
| h | 70 | 65 | 72 | 68 | 70 | 65 | 72 | 68 | 70 | 65 |
| m | 32 | 42 | 40 | 33 | 32 | 42 | 40 | 33 | 32 | 42 |
| α˚ | 60 | 45 | 45 | 60 | 60 | 45 | 45 | 60 | 60 | 45 |
|
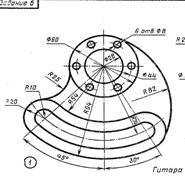
Пример выполнения
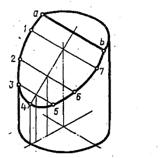
Графическая работа 4
|
| Обозна чение | № варианта | |||||||||
| d | 50 | 55 | 60 | 50 | 56 | 60 | 52 | 55 | 60 | 54 |
| h | 55 | 60 | 65 | 56 | 62 | 65 | 55 | 60 | 70 | 56 |
| а | 37 | 60 | 46 | 38 | 66 | 42 | 36 | 66 | 35 | 38 |
| α˚ | 45 | 30 | 45 | 45 | 30 | 45 | 45 | 30 | 45 | 45 |
Графическая работа 5
|
| Обозна чение | № варианта | |||||||||
| R | 45 | 40 | 42 | 45 | 42 | 40 | 45 | 44 | 40 | 45 |
| D | 80 | 90 | 88 | 85 | 95 | 45 | 80 | 94 | 45 | 85 |
| h | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| k | 110 | 110 | 110 | 100 | 110 | 110 | 110 | 110 | 110 | 100 |
Пример выполнения
Возможные варианты
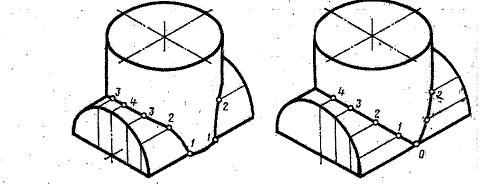
Графическая работа 6
|
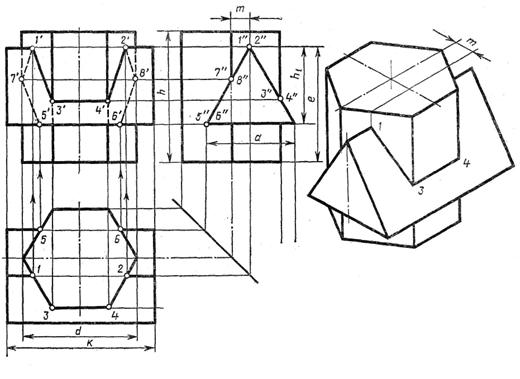
Возможные варианты
| Обозна чение | № варианта | |||||||||
| d | 55 | 54 | 70 | 56 | 55 | 54 | 70 | 56 | 54 | 56 |
| h | 65 | 72 | 70 | 68 | 64 | 72 | 68 | 68 | 65 | 71 |
| m | 10 | 8 | 15 | 16 | 10 | 8 | 14 | 16 | 9 | 8 |
| е | 55 | 72 | 75 | 60 | 56 | 72 | 76 | 60 | 55 | 71 |
| h1 | 38 | 45 | 48 | 40 | 38 | 45 | 47 | 40 | 38 | 45 |
| а | 44 | 45 | 52 | 40 | 44 | 45 | 50 | 40 | 44 | 45 |
| k | 74 | 84 | 108 | 70 | 74 | 84 | 110 | 70 | 74 | 84 |
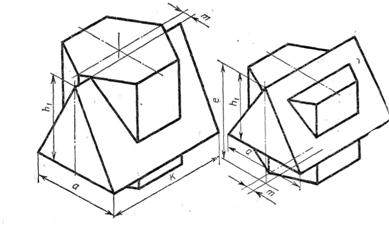
Графическая работа 7
Построить третью проекцию детали по двум заданным и ее технический рисунок с вырезом четверти
1 вариант 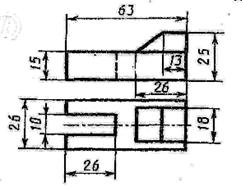 | 2 вариант 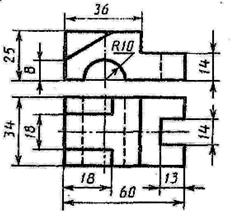 |
3 вариант 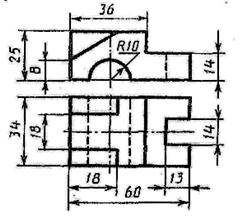 | 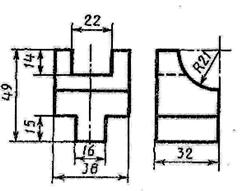 4 вариант 4 вариант |
5 вариант 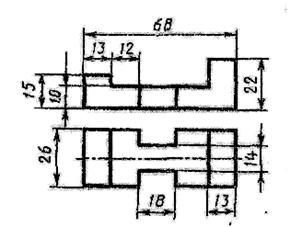 | 6 вариант 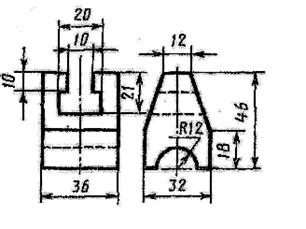 |
7 вариант 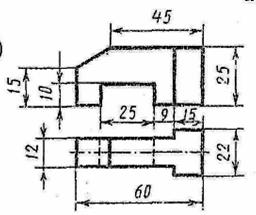 | 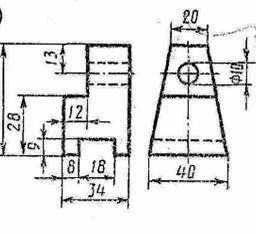 8 вариант 8 вариант |
9 вариант 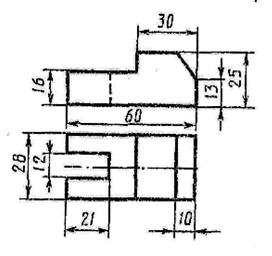 | 10 вариант 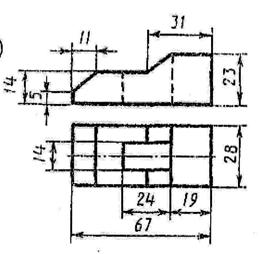 |
| Пример выполнения | |
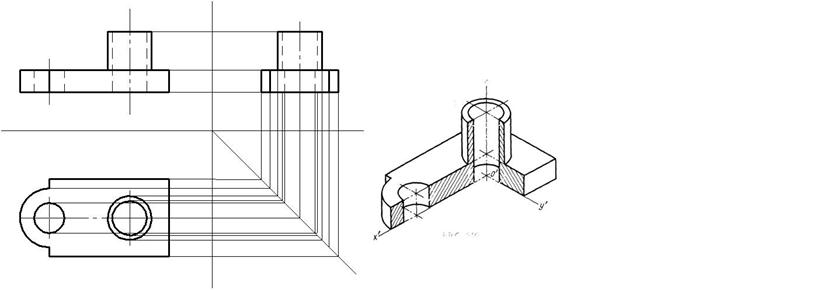 |
Утверждаю
Зам. директора по УР
_________И.Н. Матяшова
« »_______________2017год.
Инженерная графика
МЕТОДИЧЕСКОЕ РУКОВОДСТВО
по выполнению графических работ
раздела
«Геометрическое и проекционное черчение»
(1 семестр)
для студентов очного отделения
специальности 23.02.03
(индивидуальное обучение)
Разработал преподаватель Краснова Л.Г.
Красноармейск
2017г.
Содержание
Общие требования к выполнению работы
