Пересечение поверхности вращения плоскостью частного положения

Форму деталей машиностроения часто образуют срезом или вырезом части материала плоскостями из заготовок, ограниченных криволинейными поверхностями. При этом возникает необходимость построения на чертеже проекций линий пересечения поверхности плоскостью.

В случае пересечения линейчатой поверхности плоскостью в общем случае строят точки пересечения прямолинейных образующих поверхности с секущей плоскостью, т.е. решают задачу по нахождению точки пересечения прямой с плоскостью.

Если секущая плоскость – плоскость частного положения, то задача упрощается, так как одна проекция линии пересечения плоскости с кривой поверхностью уже имеется и совпадает со следом секущей плоскости. Построение недостающих проекций линии пересечения сводится к построению недостающих проекций точек на поверхности по заданным проекциям этих точек на одной из проекций поверхности.

Рассмотрим примеры.

а) Допустим, что задана поверхность прямого конуса вращения, который пересечен горизонтальной плоскостью α.

В задаче требуется построить чертёж с указанием проекций линии пересечения конуса с заданной плоскостью α..

Строим наглядное изображение(рис. 23), из которого видно, что в сечении конуса с плоскостью α получается окружность, обозначенная буквой « а» с радиусом R и центром О.

По наглядному изображению(рис. 23, слева) строим чертеж с указанием проекций линии пересечения(рис 23, справа). Фронтальная проекция линии пересечения а′′ будет расположена на фронтальном следе плоскости α, это следует из того, что плоскость α параллельна плоскости π₁.

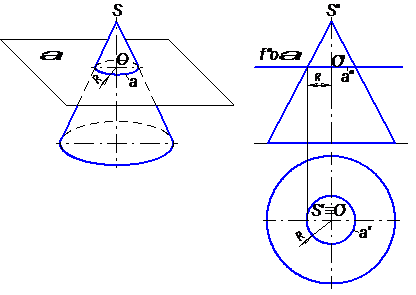
Рис. 23

Горизонтальная проекция линии пересечения а′ будет представлять собой окружность а с центром в точке О′, которая совпадает с горизонтальной проекцией вершины конуса S′.

б) Задана поверхность сферы, пересеченная фронтальной плоскостью γ (рис.24).

Требуется построить чертеж с указанием проекций линии пересечения.

Т.к. плоскость γ параллельна плоскости проекций π₂, то не трудно представить, что линией пересечения её со сферой будет окружность, обозначенная буквой а, с радиусом R, с центром О₁.

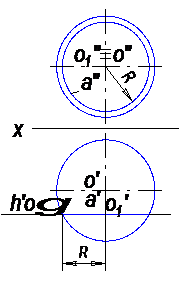
Рис.24

Горизонтальная проекция а′ линии пересечения а будет расположена на горизонтальном следе заданной плоскости γ.

Фронтальная проекция а′′ линии пересечения будет представлять собой окружность а с центром в точке О₁′′, которая совпадает с фронтальной проекцией центра сферы О′′.

в) Построим линию пересечения прямого конуса с фронтально- проецирующей плоскостью β(рис. 25). Для построения линии пересечения, находим точки пересечения образующих конической поверхности с секущей плоскостью.

Построение линии пересечения обычно выполняют в следующем порядке. Основание конуса делят на несколько равных частей, проводят горизонтальные проекции образующих и строят их фронтальные проекции.

На фронтальной проекции строят точки пересечения образующих конуса с секущей плоскостью β.

Рис. 25

Горизонтальные проекции строят в проекционной связи на соответствующих проекциях образующих – точки А′,В′,С′,D′,N′,M′ на проекциях образующих S′1′, S′2′, S′4′, S′5′, S′6′, S′8′. Горизонтальную проекцию точки на образующей S3 и симметричной точки на образующей S7 строят с помощью окружности h, проведенной на поверхности конуса через эти точки.

На фронтальной проекции большая ось АD эллипса (линии пересечения фронтально-проецирующей плоскости β с конусом) проецируется в натуральную величину, [AD]=A′′D′′. Малая ось эллипса перпендикулярна большой и проецируется в точку в середине А′′D′′. Точка О – точка пересечения большой и малой осей эллипса.

Если поверхность вращения нелинейчатая, то для построения линии пересечения такой поверхности плоскостью частного положения следует применять вспомогательные плоскости. Точки искомой линии находятся на пересечении линий, по которым вспомогательные секущие плоскости пересекут данные поверхность и плоскость.

Рассмотрим пример.

В задаче требуется построить линию пересечения сферы фронтально – проецирующей плоскостью β.

Чтобы построить её горизонтальную проекцию по известной фронтальной проекции вводят вспомогательные горизонтальные плоскости(рис. 26).

Всякое сечение сферы плоскостью есть окружность, в данной задаче это будет окружность диаметра 1-8; т.к. плоскость β наклонная, то горизонтальная проекция 1′-8′ линии пересечения будет эллипс, а фронтальная проекция – прямая линия, лежащая на фронтальном следе плоскости β. Точки 1 и 8 называют опорными, они расположены на главном меридиане сферы. Точка 1 – самая верхняя линии пересечения, а точка 8 – самая нижняя. По фронтальным проекциям – 1′′ и 8′′ найдены их горизонтальные проекции (с помощью линий связи).

Для определения горизонтальных проекций промежуточных точек вводятся вспомогательные секущие горизонтальные плоскости – γ₁, γ₂, γ₃. Для более точного построения горизонтальной проекции линии пересечения можно ввести большее количество вспомогательных плоскостей.

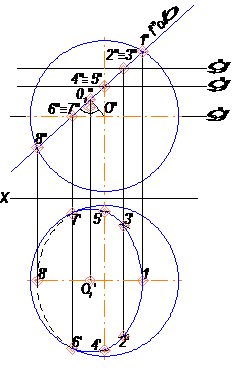
Рис. 26

Вспомогательные плоскости пересекают и поверхность сферы и секущую плоскость β. Сфера пересекается со вспомогательными плоскостями по окружностям, а плоскость β – по фронтально-проецирующим прямым. Эти окружности и фронтально-проецирующие прямые окажутся расположенными в одной плоскости или в γ₁, или в γ_2, или в γ₃ и т.д., они пересекаются и задают общие точки, принадлежащие как поверхности сферы, так и плоскости β.

Эти плоскости γ₁, γ₂, γ₃ называютсяплоскостями посредниками.

По полученным горизонтальным проекциям – 1′, 2′, 3′, 4′, 5′, 6′, 7′, 8′ проводится плавная линия – эллипс. Большая ось эллипса – линия 1-8, малая ось перпендикулярна большой оси, сначала определяется её фронтальная проекция (в середине отрезка 1′′-8′′), а её горизонтальная с помощью линии связи.

Границей видимости для 1′-8′ служат точки 6′ и 7′, лежащие на экваторе. От точки 1′ и далее до точек 6′ и 7′ часть горизонтальной проекции линии пересечения будет видимой, т.к. находится на верхней полусфере, а далее от точек 6′ и 7′ до точки 8′ будет невидимой, проведенной штриховой линией.