Принадлежность точки поверхности.

Точка на многограннике

Если нужно на обеих проекциях многогранника построить точку, лежащую на одной из его граней, то следует «связать» точку с соответствующей гранью при помощи какой-либо прямой, находящейся на этой грани.

На рисунке 8 показано построение точки К на грани АSC пирамиды SABC.

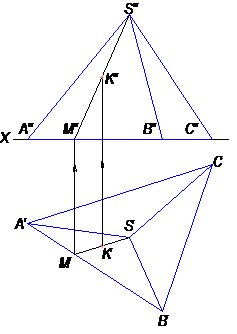
Рис. 8

По данной горизонтальной проекции (К') точки К необходимо построить ее фронтальную проекцию. Для этого через горизонтальную проекцию вершины S пирамиды и точку К' проведена горизонтальная проекция прямой SM. Затем по горизонтальной проекции прямой SM построена её фронтальная проекция, на которой и определяется с помощью линии связи фронтальная проекция точки – К''.

Точка на поверхности вращения

Положение точки на поверхности вращения определяется при помощи окружности, проходящей через эту точку на поверхности вращения.

Возможно применение прямолинейных образующих в случае линейчатых поверхностей вращения, подобно тому, как это показано на рисунке 9.

Рис. 9

На рисунке 10 показано нахождение проекций точек на сфере. По данной проекции А′ точки А построена фронтальная проекция – А′′; по данной проекции В′′ найдена горизонтальная проекция В′ точки В, удовлетворяющей дополнительному условию, что точка В невидима при фронтальном проецировании.

Точка С задана на экваторе; её проекция С′ находится на очерке горизонтальной проекции сферы, т.е. на горизонтальной проекции экватора.

Точка К лежит на главном меридиане; она принадлежит параллели, на которой находится точка А.

Точка D также находится на главном меридиане, причем она невидима при горизонтальном проецировании.

Рис. 10

Пересечение прямой с плоскостью.

Пересечение прямой с проецирующей плоскостью

При построении точки пересечения прямой с проецирующей плоскостью исходят из того, что плоскость, перпендикулярная плоскости проекций, проецируется на нее в виде прямой линии. Следовательно, на этой прямой находится и соответствующая проекция точки пересечения заданной прямой с проецирующей плоскостью. Построение точки пересечения прямой с проецирующей плоскостью рассмотрим на примере (рис.11).

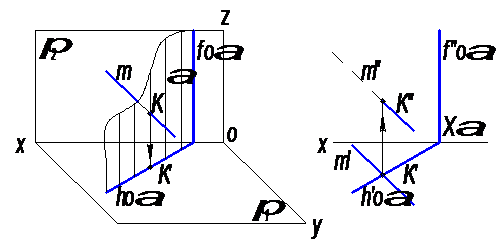
а) б)

Рис. 11

На рисунке 11б задана следами горизонтально – проецирующая плоскость α и прямая m общего положения (аксонометрическое изображение на рис. 11а). Точка их пересечения К принадлежит и прямой m, и плоскости α. Следовательно, ее горизонтальная проекция К′ принадлежит и горизонтальному следу плоскости h_oα, т. к. α _┴ π₁, и горизонтальной проекции прямой – m′. По горизонтальной проекции точки – К′ находим ее фронтальную проекцию – К′′ на фронтальной проекции прямой – m′′.

По горизонтальной проекции видно, что левее точки К, прямая m находится за плоскостью α, которая закрывает этот участок прямой на фронтальной проекции. Условно считают плоскость α не прозрачной, поэтому на чертеже фронтальная проекция прямой левее К′′ показана как невидимая, штриховой линией. На горизонтальной проекции вся прямая m видимая.

Здесь необходимо отметить собирательное свойство проецирующих плоскостей: все, что находится в горизонтально-проецирующей плоскости (точка, прямая, кривая…) спроецируется на горизонтальную плоскость проекций на горизонтальный след этой плоскости.

Все, что находится во фронтально-проецирующей плоскости спроецируется на фронтальную плоскость проекций на фронтальный след этой плоскости.

Все, что расположено в профильно-проецирующей плоскости спроецируется на профильную плоскость проекций на профильный след этой плоскости.